Traité projectif des coniques - Définition

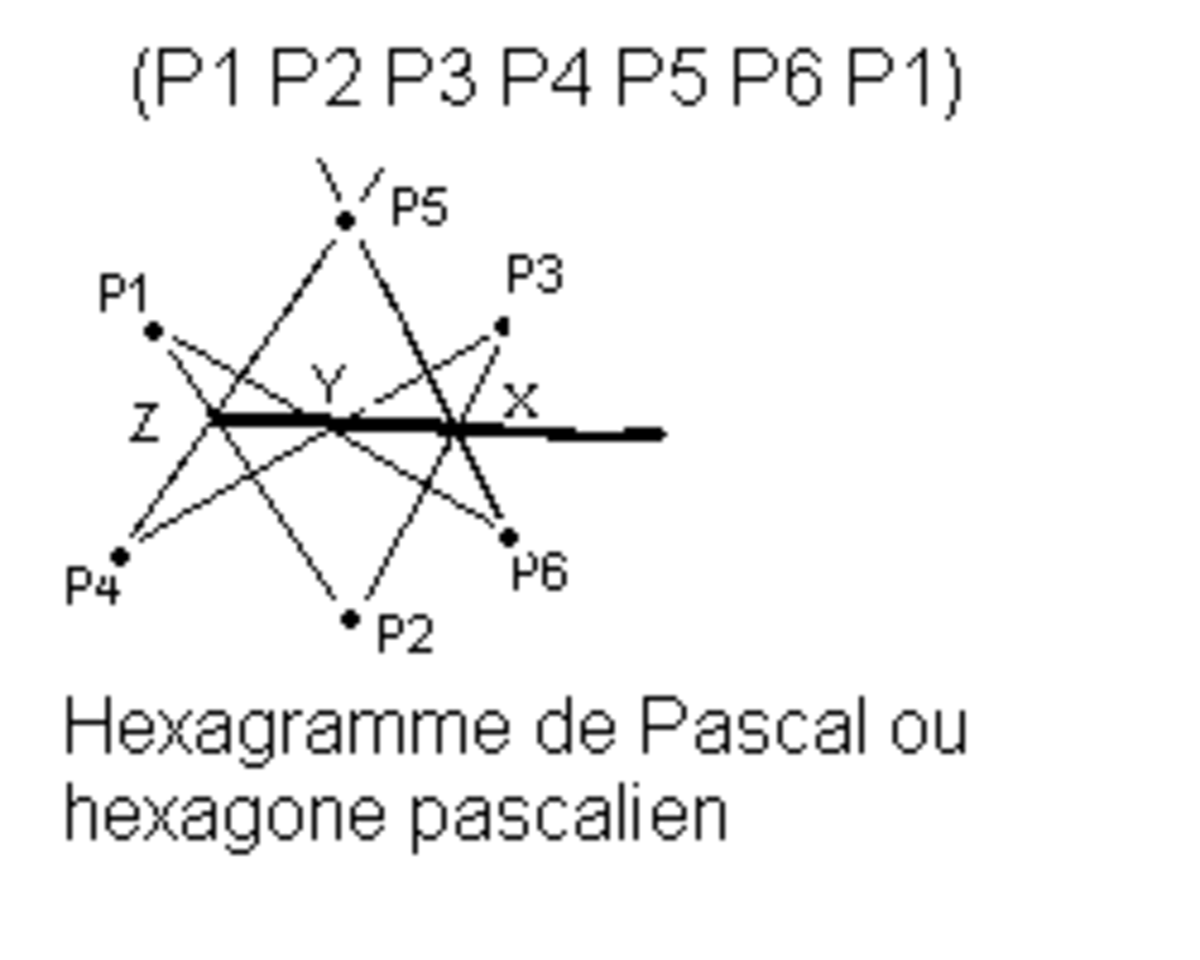
Anticipation : hexagone de Brianchon et hexagramme de Pascal

Les trois questions importantes que posent les coniques sont :

• intersection avec une droite
• tangente en un point
• nombre de points nécessaires et suffisants pour définir une conique ?

Annonçons tout de suite avant de les démontrer deux grands théorèmes des coniques. Soit un hexagone inscrit dans une conique. Soient A, B et C les points d'intersection des côtés opposés de l'hexagone s'ils existent. Le théorème de Pascal affirme que A, B et C sont alignés. La droite que forme cet alignement est appelée droite de Pascal. La figure obtenue par la construction est appelée hexagramme mystique. Ce théorème est le dual du théorème de Brianchon qui s'énonce ainsi : les diagonales joignant les sommets opposés d'un hexagone sont concourantes si et seulement si cet hexagone est circonscrit à une conique.

Questions soulevées par l'explosion combinatoire.

La configuration de Pappus offre une forte permutation : il y a 6 hexagrammes non dégénérés (A1 C2 B1 A2 C1 B2 ; A1 C2 B1 B2 C1 A2 ; A1 B2 B1 C2 C1 A2 ; A1 B2 B1 A2 C1 C2 ; A1 A2 B1 B2 C1 C2 ; A1 A2 B1 C2 C1 B2 ), donc 6 droites de Pappus. Quelles sont les propriétés de ces 6 droites ? En fait on peut démontrer qu'elles sont concourantes en deux groupes de 3. Mais de quels axiomes minimaux a-t-on besoin pour démontrer cette propriété ? L'axiome fondamental de la géométrie projective est-il indispensable ? L'axiome de Desargues suffirait-il ? Quant à l'hexagramme de Pascal, de nombreux mathématiciens du XIX^e siècle se sont penchés sur les diverses permutations du parcours des 6 points. Il s'agit particulièrement de Bauer, Catalan, Cayley, Fontaneau, Gräfe, Grossmann, Hesse, Jörres, Kirkman, Ladd-Franklin-Christine, Little  , Lüroth, Meyer, Molk, Plücker, George Salmon, Jakob Steiner, Veronese-G., von Staudt. Avec 6 points, on peut réaliser 60 parcours hexagonaux, donc 60 droites de Pascal. Quelles sont les propriétés de ces 60 droites, comment sont disposées leurs intersections dans le plan ? Quel rapport avec les 60 points de Brianchon que l'on peut dualement envisager ? Par exemple Steiner a montré qu'elles sont concourantes 3 à 3, d'où 20 «points de Steiner». Comment sont disposés ces points, à quel sous-ensemble de permutation correspond chaque point ? Quelles sont leur 20 polaires, ont-elles un rapport avec les 60 droites de Pascal? Ce regroupement par 3 peut-il, comme celui de la figure de Pappus, être démontré par l'axiome de Desargues ou doit-on faire appel à l'axiome fondamental de la géométrie projective ? Ces propriétés ont-elles un lien avec la conservation du rapport anharmonique sur une conique ? Comment, à partir de la découverte de la perspective à la Renaissance en est-on arrivé à se poser ce type de problématique?

Plan projectif pappusien et coniques.

Voir Traité projectif des coniques/Dans un plan pappusien.

• Substitution de deux voisins.

• Existe-t-il une tangente dans un plan projectif pappusien? (Oui)

• Intersection droite/conique dans un plan projectif pappusien.

• Polaire dans un plan projectif pappusien.
• Hexagrammes mystiques et géométrie euclidienne.

Voir Traité projectif des coniques/Dans un plan pappusien--->

Ce que l'on sait de l'approche de Pascal lui-même

• Pascal, Œuvres complètes, Bibliothèque de la Pléiade, Paris, Gallimard, nouvelle édition de 1998 par Michel le Guern.

Blaise Pascal (1623-1662) durant sa courte vie a écrit quatre traités de géométrie dont un est perdu, malheureusement c'est celui qui approfondissait les coniques.