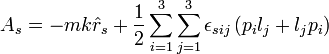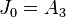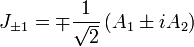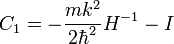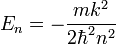Vecteur de Runge-Lenz - Définition

Constantes du mouvement et superintégrabilité

Les sept grandeurs scalaires E, A et L (étant de vecteurs, les deux dernières comptent comme trois grandeurs conservées chacune) sont reliées par deux équations A · L = 0 et A² = m²k² + 2 m E L², ce qui laisse 5 constantes du mouvement indépendantes. Ceci est cohérent avec les six conditions initiales du système (la position initiale et le vecteur vitesse initiale ayant chacune trois composantes) qui détermine l'orbite de la particule puisque la date initiale ne peut pas être déterminée par une constante du mouvement. Étant donné que la norme de A (et donc l'excentricité e de l'orbite) peut être déterminée par le moment cinétique L et l'énergie E, seule la direction de A est conservée indépendamment ; en outre, comme A doit être perpendiculaire à L, il ne fournit en fait qu'une seule constante du mouvement.

Un système mécanique à d degrés de liberté peut avoir au maximum 2d - 1 constantes du mouvement indépendantes, puisqu'il y a 2d conditions initiales et que la date initiale ne peut être déterminée par une constante du mouvement. Un système qui possède plus de d constantes du mouvement est appelé superintégrable et un système à 2d − 1 constantes est dit maximalement superintégrable.

Puisque l'équation de Hamilton-Jacobi dans un système de coordonnées ne mène qu'à d constantes du mouvement, les systèmes intégrables sont séparables dans plus d'un système de coordonnées Le problème de Kepler est maximalement superintégrable puisqu'il possède 3 degrés de liberté et 5 constantes du mouvement indépendantes ; son équation de Hamilton-Jacobi est séparable à la fois en coordonnées sphériques et en coordonnées paraboliques. Les systèmes maximalement superintégrables mènent à des orbites fermées à une dimension dans l'espace des phases, puisque l'orbite est l'intersection des iso-surfaces de leurs constantes du mouvement dans l'espace des phases. Ce systèmes peuvent être quantifiés canoniquement en utilisant uniquement des relations de commutation comme expliqué.

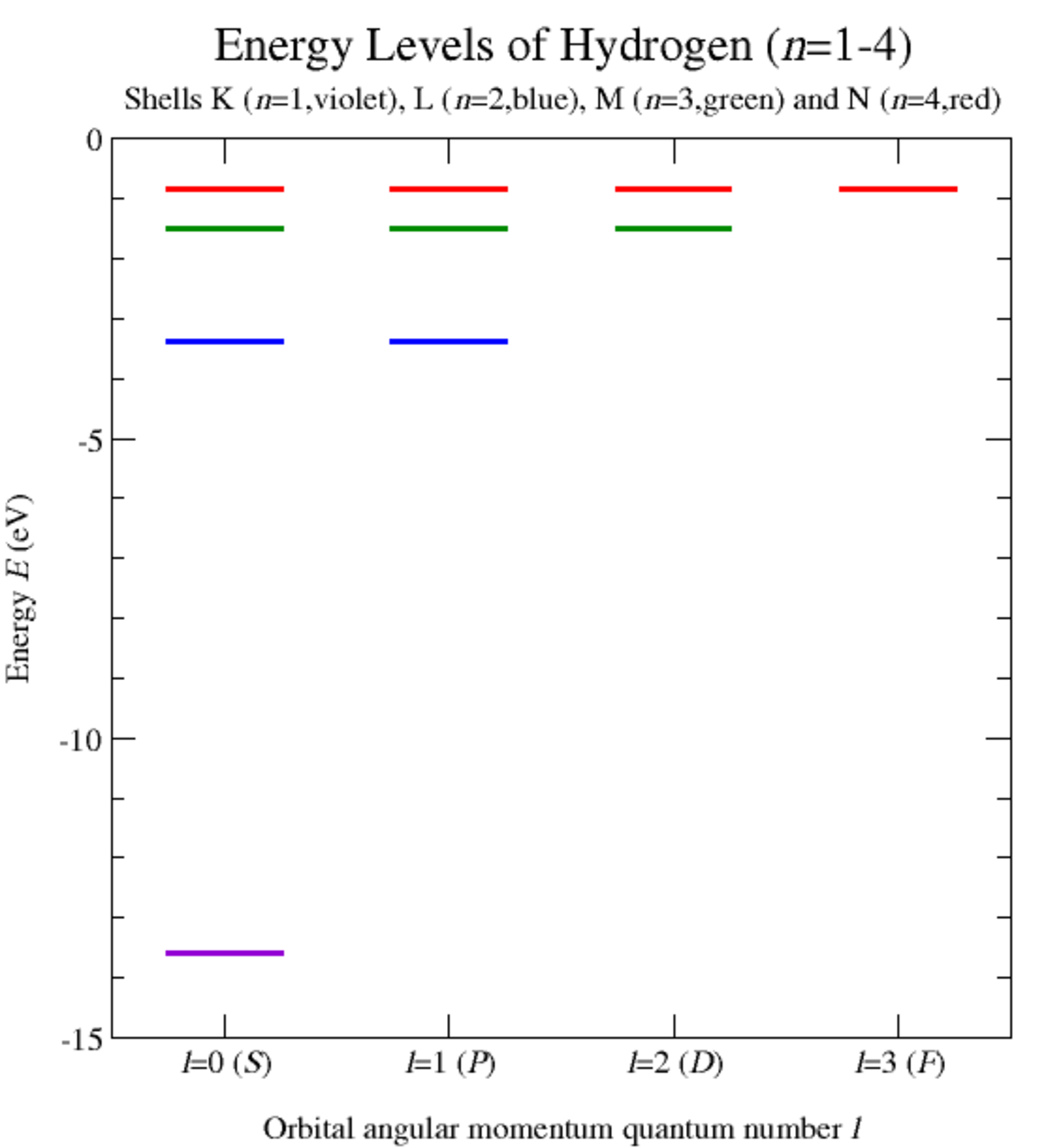
Mécanique quantique de l'atome d'hydrogène

Figure 6: Niveaux d'énergie de l'atome d'hydrogène tels que prévus par les relations de commutation des opérateurs moment cinétique et vecteur de Runge-Lenz ; ces niveaux d'énergie ont été vérifiés expérimentalement.

Les crochets de Poisson fournissent une méthode simple de quantification canonique d'un système mécanique ; la relation de commutation de deux opérateurs quantiques est égal au crochet de Poisson des variables classiques correspondantes multiplié par . En menant le calcul de cette quantification et en déterminant les valeurs propres de l'opérateur de Casimir C₁ du problème de Kepler, Wolfgang Pauli a obtenu spectre énergétique des atomes hydrogénoïdes (Figure 6) et donc leur spectre d'émission atomique Ce résultat élégant a été obtenu avant le développement de la mécanique ondulatoire.

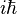
Une subtilité de l'opérateur quantique associé au vecteur de Runge-Lenz A est que les opérateurs impulsion et moment cinétique ne commutent pas ; le produit vectoriel de p et L doit alors être défini avec précaution. Généralement, les opérateurs pour les composantes cartésiennes A_s sont définis en utilisant un produit symétrique :

à partir desquels les opérateurs d'échelle correspondant peuvent être définis

Un premier opérateur de Casimir normalisé peut de la même manière être défini

où H⁻¹ est l'inverse de l'opérateur énergie hamiltonien et I est l'opérateur identité. En appliquant cet opérateur aux états propres des opérateurs moment cinétique total, moment cinétique azimutal et énergie, les valeurs propres du premier opérateur de Casimir C₁ sont n² - 1 ; elles sont indépendantes des nombres quantiques l et m, rendant les états d'énergies dégénérés. Les états d'énergie sont donnés par

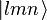
ce qui est équivalent à la formule de Rydberg pour les atomes hydrogénoïdes (Figure 6).