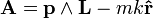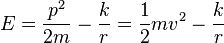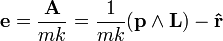Vecteur de Runge-Lenz - Définition
La liste des auteurs de cet article est disponible ici.
Définitions mathématiques
Pour une particule seule mise en mouvement par une force centrale en carré inverse de la distance décrite par l'équation
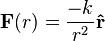
où
-
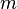
-

-
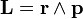
-
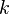
-
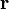
-
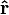
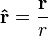
Étant donné que la force est supposée conservative, l'énergie totale E est une constante du mouvement
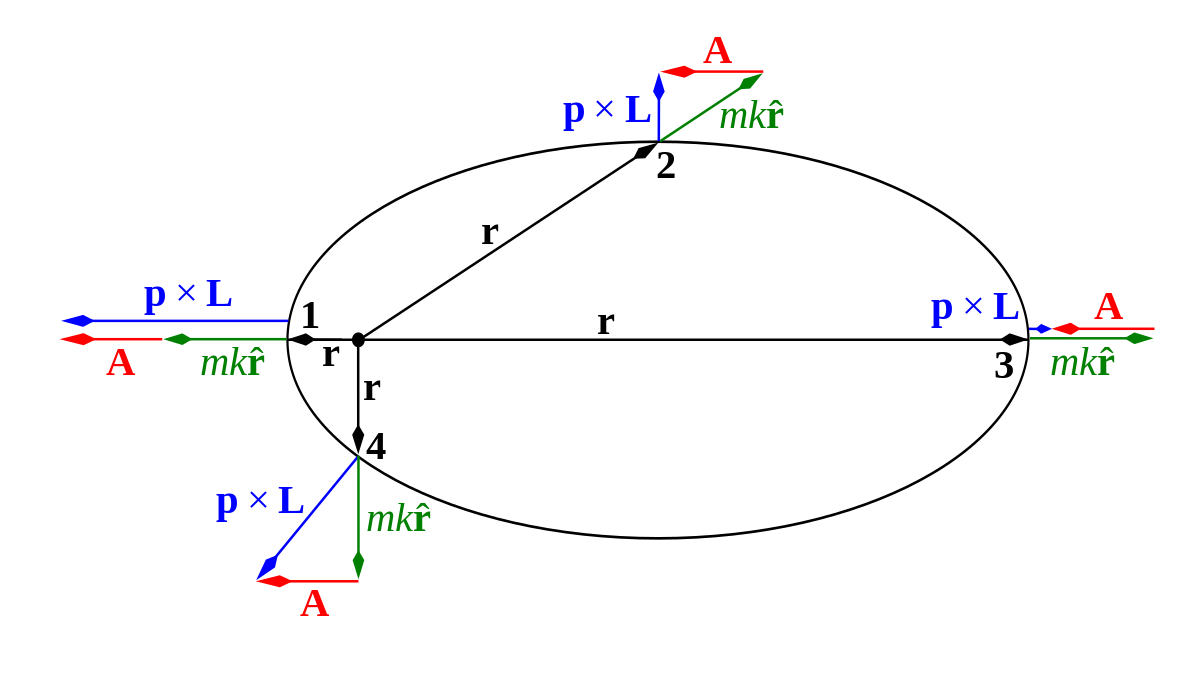
De plus la force étant centrale, le moment cinétique L est également constant et définit le plan dans lequel la particule se déplace. Le vecteur de Runge-Lenz est perpendiculaire à L car p ∧ L et r sont perpendiculaires à L. Il s'ensuit que A est contenu dans le plan de l'orbite.
Cette définition de A est applicable pour une particule seule et ponctuelle de masse m se déplaçant sous l'effet d'une force donnée. Cependant la même définition peut être étendue au problème à deux corps, tel que le problème de Kepler, en prenant pour m la masse réduite des deux corps et pour r le vecteur entre les deux corps.
Une alternative pour la même constante du mouvement est également possible. La plus commue est de diviser par mk pour définir le vecteur excentricité
Histoire des redécouvertes
Le vecteur de Runge-Lenz A est une constante du mouvement du problème de Kepler, utile pour décrire les orbites astronomiques, telles que le mouvement des planètes. Néanmoins son usage n'a jamais été très répandu parmi les physiciens peut-être parce qu'il est moins intuitif que la quantité de mouvement ou le moment cinétique. C'est la raison pour laquelle il a été redécouvert plusieurs fois au cours des trois derniers siècles. Jakob Hermann est le premier à montrer que A est conservé dans le cas particulier des forces centrales en carré inverse, et travailla sur ses connexions avec l'excentricité orbitale dans le cas des orbitales elliptiques. Les travaux de Hermann sont généralisés dans leur forme moderne par Jean Bernoulli en 1710. À la fin du XVIIIe siècle, Pierre-Simon de Laplace redécouvre la conservation de A, l'obtenant de manière analytique et non plus de façon géométrique. Vers le milieu du XIXe siècle, William Rowan Hamilton détermine le vecteur excentricité, qui est équivalent, et l'utilise pour montrer que le vecteur quantité de mouvement p décrit un cercle pour un mouvement effectué sous une force centrale en carré inverse (Figure 3). Au début du XXe siècle, Josiah Willard Gibbs trouve le même vecteur par analyse vectorielle. La méthode de Gibbs est citée en exemple par Carl Runge dans un livre allemand sur les vecteurs qui fut référencé par Wilhelm Lenz dans son article sur le traitement quantiquel de l'atome d'hydrogène. En 1926, le vecteur est utilisé par Wolfgang Pauli pour déterminer le spectre de l'hydrogène en utilisant la mécanique matricielle et non l'équation de Schrödinger ; après l'article de Pauli il commence à être connu sous le nom de vecteur de Runge–Lenz.