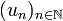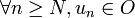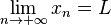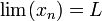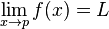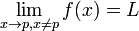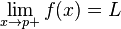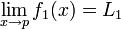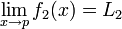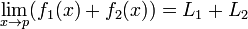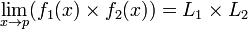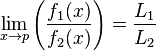Limite (mathématiques) - Définition
En mathématiques, rechercher la limite d'une suite ou d'une fonction, c'est déterminer si cette suite ou cette fonction s'approche d'une valeur particulière lorsque la variable prend des valeurs extrêmes. Dans cette définition très intuitive, deux notions restent à définir avec précision : la notion de s'approcher et celle de valeur extrême.
Historiquement, les mathématiques se sont initialement intéressées aux limites de suites, on cherchait à savoir, si, pour les grandes valeurs de l'indice, les termes de la suite se rapprochaient d'une valeur particulière, c'est-à-dire, si à partir d'un certain rang, on était aussi proche que l'on veut de cette valeur particulière. La notion de proximité est liée à une distance qui dans R est définie par la valeur absolue d'une différence, mais cette notion peut se généraliser à tout espace métrique. Plus tard, la notion s'est étendue aux espace topologiques et " être proche " signifie alors " être dans un voisinage arbitrairement choisi ".
Ensuite est intervenue la notion de limite de fonction, initialement rattachée à la limite de suite. Pour chercher la limite d'une fonction quand la variable s'approche de a, on cherchait à déterminer la limite de la suite (f(un)) pour toute suite (un) dont la limite était a. La complexité de cette approche, la multiplicité des cas, ont conduit à définir la notion de limite de fonction indépendamment de celle de limite de suite. Pour pouvoir manipuler la notion de limite et l'exploiter sans erreur, il a été nécessaire de la définir de manière plus précise et plus formelle. C'est ainsi que cet article présente une définition formelle de la limite d'une suite convergente, de la limite d'une fonction à valeurs dans R, la notion de limite infinie, et présente le cas de l'espace métrique et de l'espace topologique.
Voir aussi, pour une présentation plus abordable, l'article limite dans la série Mathématiques élémentaires.
Limite d'une suite de nombres réels
Supposons que (x1, x2, ...) soit une suite de nombres réels. On dit que cette suite est convergente, si par définition :
il existe un réel L tel que
- pour tout réel ε>0 il existe un entier naturel n0 (qui dépend de ε) tel que pour tout entier n>n0 on ait |xn - L| < ε.
Intuitivement, cela signifie que tous les termes de la suite deviennent aussi proches que l'on veut d'un réel L, dès que n est assez grand; la valeur absolue |xn - L| doit être interprétée comme la " distance " entre xn et L.
On démontre que, pour une suite convergente, le réel L de la définition est unique. Ce réel L est appelé la limite de cette suite et on écrit :
ou
Toutes les suites ne sont pas convergentes et, dans le cas où une suite n'est pas convergente, elle est dite non convergente ou divergente. Certains préfèrent réserver le terme divergent aux suites non convergentes non bornées.
Exemples
- La suite (1/1, 1/2, 1/3, 1/4, .) de nombres réels est convergente de limite 0.
- La suite (3, 3, 3, 3, 3, ...) est convergente de limite 3.
- La suite (1, -1, 1, -1, 1, ...) est non convergente
- La suite (1, -2, 3, -4, 5, ...) est divergente.
- La suite (1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, 1/2 + 1/4 + 1/8 + 1/16, ...) est convergente de limite 1. Cette suite est un exemple de série.
- Si a est un nombre réel de valeur absolue |a| < 1, alors la suite de terme général an a une limite 0.
Si a > 0 , alors la suite de terme général a1/n a une limite égale à 1.
Propriétés
Théorème de la continuité séquentielle:
Une fonction f : R → R est continue en un point L si et seulement si :
- pour toute suite réelle (xn) convergente de limite L, la suite (f(xn)) est convergente de limite f(L).
Une sous-suite (ou suite extraite) de la suite (xn) est une suite de la forme (xa(n)) où les a(n) sont des entiers naturels tels que pour tout n on ait a(n) < a(n+1). Intuitivement, une sous-suite s'obtient à partir de la suite initiale en omettant certains termes. Une suite est convergente si et seulement si toutes ses sous-suites sont convergentes et ont même limite.
L'opération de passage à la limite est linéaire dans le sens suivant : si (xn) et (yn) sont des suites réelles convergentes et que lim xn = L et lim yn = P, alors la suite (xn + yn) est aussi convergente et a pour limite L + P. Si a est un nombre réel, alors la suite (a xn) est convergente de limite aL. Ainsi, l'ensemble c de toutes les suites réelles convergentes est un espace vectoriel réel et l'opération de passage à la limite est une forme linéaire sur c à valeurs réelles.
Si (xn) et (yn) sont des suites réelles convergentes de limites respectives L et P, alors la suite (xnyn) est convergente de limite LP. Si ni P ni aucun des termes yn n'est nul, alors la suite (xn/yn) est convergente de limite L/P.
Toute suite convergente est une suite de Cauchy et est ainsi bornée. Si (xn) est une suite de réels, bornée et croissante (i.e. pour tout entier n, xn ≤ xn+1), alors elle est nécessairement convergente.
Toute suite de Cauchy de nombres réels est convergente, ou plus simplement : l'ensemble des réels est complet.
Une suite de nombres réels est convergente si et seulement si ses limites inférieures et supérieures sont finies et égales.
Limite d'une fonction en un point
Supposons que f : U → R soit une fonction, où U est un sous-ensemble de l'ensemble des réels. Si p est un point de U (point d'accumulation de U). On dit que f admet une limite (finie) au point p, s'il existe un réel L vérifiant
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans U tel que |x - p| < δ, on ait |f(x) - L| < ε.
On démontre que ce réel L de la définition est unique et on l'appelle limite de f au point p. On le note :
Ceci équivaut à dire:
- pour tout suite convergente (xn) dans U de limite égale à p, la suite (f(xn)) est convergente de limite L.
Remarquons que la fonction n'a pas besoin d'être définie en p, mais si la fonction est définie en p alors f(p) est égale à la limite de f en p et donc l'application est continue en p.
Définissons maintenant la limite pointée :
On dit que f admet une limite pointée (finie) au point p, s'il existe un réel L vérifiant
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans U tel que 0 < |x - p| < δ, on ait |f(x) - L| < ε.
De même ce nombre L est alors unique et on note :
Occasionnellement, il peut être utile d'approcher le point p que d'un seul côté.
On dit que f admet une limite à droite (finie) au point p, s'il existe un réel L vérifiant
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans U tel que 0 < x - p < δ, on ait |f(x) - L| < ε.
Ce nombre L est alors unique et on le note :
Les limites à gauche s'obtiennent en remplaçant x - p dans la dernière définition par p - x.
Il est possible aussi de considérer des limites où p ou L sont égaux à plus ou moins l'infini. On dit que f(x) tend vers plus l'infini (+∞) quand x tend vers p si par définition
- pour tout réel R > 0, il existe un réel δ > 0 tel que pour tout x tel que |x - p| < δ on ait f(x) > R.
On dit que la limite de f(x) quand x tend vers plus l'infini est égal à L si
- pour tout réel ε > 0 il existe un réel S > 0 tel que pour tout x > S, on ait |f(x) - L| < ε.
Enfin, on dit que la limite de f(x) est égale à plus l'infini quand x tend vers plus l'infini, si
- pour tout réel R > 0 il existe un réel S > 0 tel que pour tout x tel que x > S, on ait f(x) > R.
Les définitions pour moins l'infini sont analogues.
En remplaçant ε par S comme précédemment, on peut aussi définir les limites infinies d'un seul côté (à droite ou à gauche).
Exemples
- La limite de
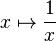
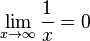
- Les limites à droite et à gauche de
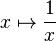
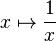

- La limite de
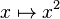
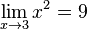
- La limite de
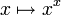
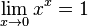
- La limite de
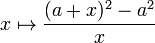
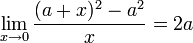
- La limite à droite de
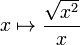
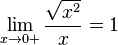
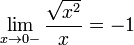
- La limite de
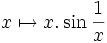
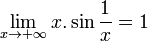
- La limite de
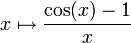
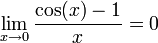
Propriétés
La limite pointée de f(x) quand x tend vers p existe si et seulement si les limites à droite et à gauche en p existent et sont égales.
Si p est un point de U, alors la limite de f(x) quand x tend vers p existe si et seulement si les limites à droite et à gauche en p existent et sont égales à f(p), si et seulement si la limite pointée de f(x) quand x tend vers p existe et est égale à f(p) et si et seulement si f est continue en p.
Si p n'appartient pas U alors la limite de f(x) quand x tend vers p existe si et seulement si les limites à droite et à gauche en p existent et sont égales.
Le passage à la limite des fonctions est compatible avec les opérations algébriques :
Si
et
alors
et
et
(La dernière propriété suppose que f2 ne s'annule pas dans un voisinage de p et que L2 n'est pas nul).
Ces propriétés sont aussi valables pour les limites à droite et à gauche, pour le cas p = ±∞, et aussi pour les limites infinies en utilisant les règles suivantes :
- q + ∞ = ∞ pour q ≠ -∞
- q × ∞ = ∞ si q > 0
- q × ∞ = -∞ si q < 0
- q / ∞ = 0 si q ≠ ± ∞
(voir la droite réelle achevée).
Remarquons qu'il n'y a pas de règle générale pour le cas q / 0; cela dépend de la façon dont on s'approche de 0. Certains cas comme par exemple 0/0, 0×∞ ∞-∞ ou ∞/∞, ne sont pas non plus couverts par ces règles mais les limites peuvent être en général obtenues par la règle de L'Hôpital.
Indétermination
Il existe certaines formes de limite où il est n'est pas possible de conclure directement en utilisant des opérations sur les limites, ce sont les formes dites indéterminées.
Indétermination de la forme 0/0 quand le résultat obtenu donne 0/0
Indétermination de la forme ∞/∞ quand le résultat obtenu donne ∞/∞
Indétermination de la forme ∞ - ∞ quand le résultat obtenu donne ∞ - ∞
Indétermination de la forme 0 × ∞ qui se ramène aux deux premiers cas en remarquant qu'une multiplication par 0 équivaut à une division par l'infini, ou qu'une multiplication par l'infini équivaut à une division par 0
Indétermination de la forme 00 qui se ramène au cas précédent en remarquant que ab peut s'écrire eb×ln(a) et que la limite de b×ln(a) est alors de la forme 0 × ∞
On peut utiliser la règle de L'Hôpital pour lever une indétermination lors d'un calcul de limite.
Espaces métriques
Les nombres réels forment un espace métrique si nous utilisons la fonction distance définie par la valeur absolue : d(x,y) = |x - y|. Il en est de même des nombres complexes avec le module. De plus, l'espace euclidien Rn forme un espace métrique avec la distance euclidienne. Voici quelques exemples motivant une généralisation des définitions de limite données précédemment.
Si (xn) est une suite dans un espace métrique (M, d), alors on dit que la suite a une limite L si par définition pour tout réel ε>0 il existe un entier naturel n0 tel que pour tout entier n>n0 on ait d(xn, L) < ε.
Si l'espace métrique (M, d) est complet (ce qui est le cas pour l'ensemble des nombres réels ou complexes et l'espace euclidien, et tout autre espace de Banach, alors on peut établir la convergence d'une suite de M en montrant que c'est une suite de Cauchy. L'avantage de cette approche est de pouvoir montrer que la suite est convergente sans nécessairement connaître la limite d'avance.
Si M est un espace vectoriel normé réel ou complexe, alors l'opération de passage à la limite est linéaire, comme nous l'avons expliqué ci-dessus dans le cas des suites de nombres réels.
Maintenant supposons que f : M → N soit une application entre deux espaces métriques, et que p soit un élément de M et L un élément de N. On dit que la limite de f(x) quand x tend vers p est égale à L et on écrit :
si par définition :
- pour tout réel ε > 0 il existe un réel δ > 0 tel que pour tout x dans M tel que d(x, p) < δ, on ait d(f(x), L) < ε.
Ce qui est équivalent à
- pour toute suite convergente (xn) de M telle que la limite soit égale à p, la suite (f(xn)) est convergente de limite L.
Une fonction f est continue en p si et seulement si la limite de f(x) quand x tend vers p existe et est égale à f(p). De manière équivalente, f transforme toute suite de M convergente de limite p en une suite de N convergente de limite f(p).
À nouveau, si N est un espace vectoriel normé, alors l'opération de passage à la limite est linéaire dans le sens suivant : si la limite de f(x) quand x tend vers p est égale à L et la limite de g(x) quand x tend vers p est égale à P, alors la limite de f(x) + g(x) quand x tend vers p est égale à L + P. Si a est un scalaire du corps de base, alors la limite de af(x) quand x tend vers p est égale à aL.
Si N est égal à R, alors nous pouvons définir des limites infinies; si M est égal à R, alors nous pouvons définir des limites à droite et à gauche de manière analogue aux définitions précédentes.
Exemples
- Si z est un nombre complexe de module |z| < 1, alors la suite ( z, z2, z3, ...) de nombres complexes converge et a pour limite 0. Géométriquement, ces nombres se rapprochent de l'origine en suivant une "spirale logarithmique".
- Dans l'espace métrique C[a,b] de toutes les fonctions continues définies sur l'intervalle [a,b], muni de la distance de la convergence uniforme, tout élément peut être écrit comme limite d'une suite de fonctions polynomiales. C'est ce qu'affirme le théorème de Stone-Weierstrass.
Généralisations pour les espaces topologiques
Toutes les notions de limite ci-dessus peuvent être unifiées et généralisées à un espace topologique arbitraire en introduisant les filtres et leur limite.
Néanmoins la définition de limite pour le cas particulier des suites (indexées par

- Une suite
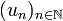
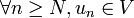
On peut donner une définition équivalente à l'aide des bases de voisinages :
- Etant donné
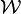
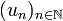
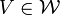
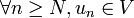
Cette définition peut aussi être reformulée en terme d'ouverts :
- Une suite