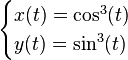Astroïde - Définition
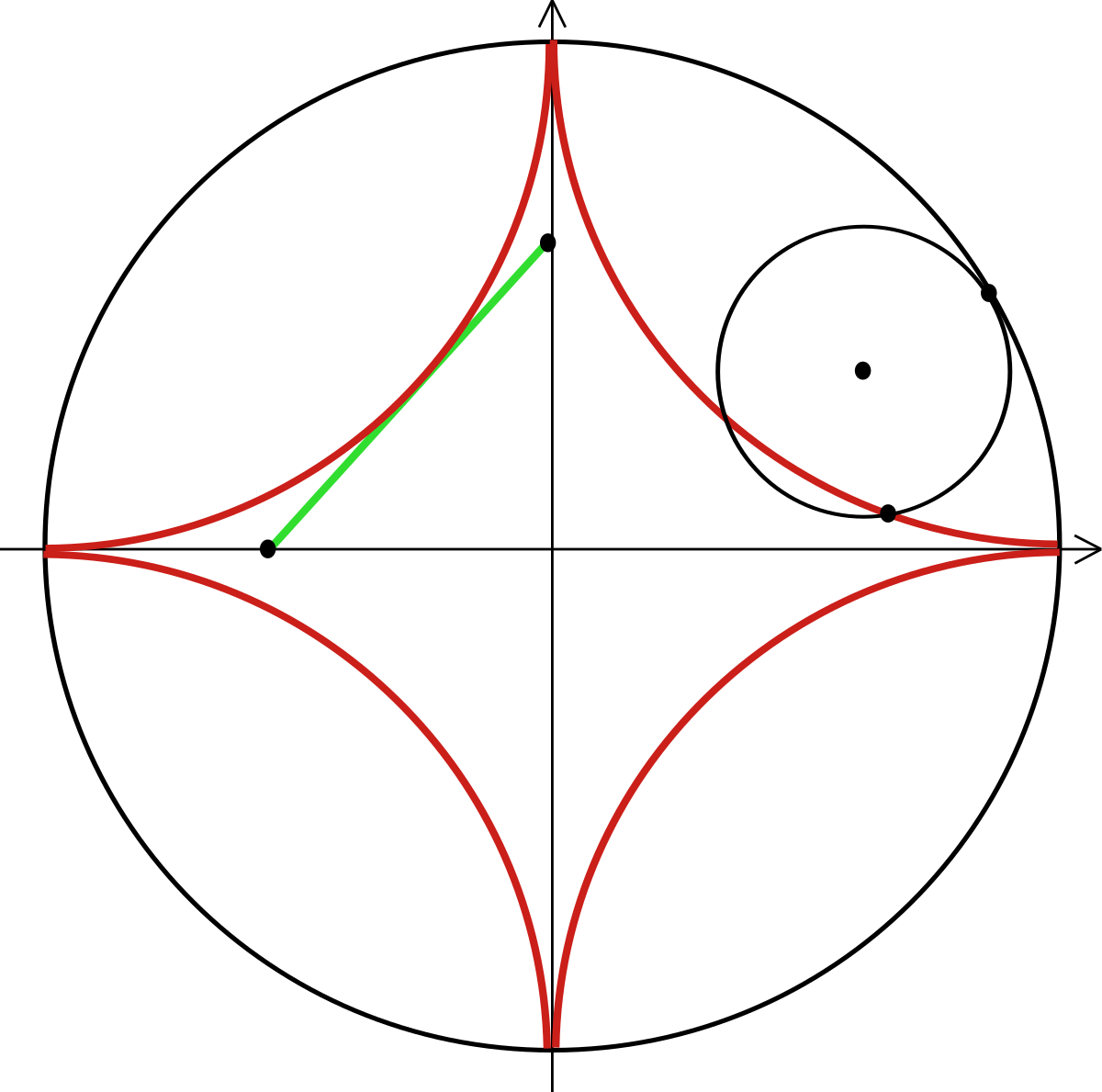
Une astroïde est une courbe plane, qui peut se définir de plusieurs façons. En particulier, il est possible de l'obtenir en faisant rouler un cercle de rayon ¼ à l'intérieur d'un cercle de rayon 1. Pour cette raison, l'astroïde est une hypocycloïde de cercle à quatre points de rebroussement.
Une astroïde peut être définie par l'équation paramétrique suivante :
Sur la figure ci-contre a été tracé en vert un segment de longueur 1 reliant un point de l'axe des abscisses à un point de l'axe des ordonnées. Il est tangent à l'astroïde. Pour cette raison, l'astroïde peut être vue comme la courbe enveloppe de la famille des segments vérifiant ces propriétés. Pour décrire cette famille par une image, on évoque souvent une échelle glissant le long d'un mur.
L'astroïde admet pour équation cartésienne
- (x2 + y2 − 1)3 + 27x2y2 = 0.
C'est une courbe algébrique de degré égal à six et de genre zéro (une sextique rationnelle).
| Exemples de courbes | |||
| Coniques dont Cercle - Ellipse- Parabole - Hyperbole | |||
| Cardioïde - Cissoïde - Clothoïde - Cycloïde - Épicycloïde - Hypocycloïde (Astroïde, Deltoïde)
- Hypotrochoïde - Spirale (dont Spirale logarithmique, Spirale d'Archimède) - Hélice |
|||
| Lemniscate (dont Lemniscate de Gerono, Lemniscate de Booth, Lemniscate logarithmique, Courbe du diable) | |||
| Trajectoire - Ovale de Cassini - Chaînette - Courbe brachistochrone | |||
| Accéder au portail de la géométrie | |||