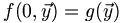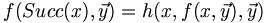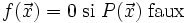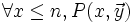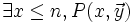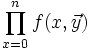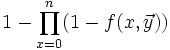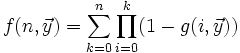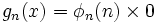Fonction récursive primitive - Définition

Définition d'une fonction récursive primitive

On s'intéresse aux fonctions définies sur l'ensemble des entiers naturels, ou sur les ensembles des k-uplets d'entiers naturels, et à valeurs dans .

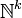
On construit les fonctions récursives primitives de proche en proche en partant des trois fonctions de base :

• La fonction identiquement nulle

• La fonction Successeur : Succ(t) = t + 1

• Les projections :

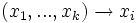
et en itérant les deux constructions suivantes :

• La composition de fonctions : si g₁, g₂, ..., g_k sont récursives primitives sur et si h est récursive primitive sur , toutes déjà définies, alors la fonction f = h(g₁,...,g_k) est une nouvelle fonction récursive primitive définie sur .

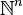
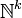
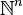
• La définition récursive d'une fonction : Si g est récursive primitive sur , et h récursive primitive sur , on définit une nouvelle fonction récursive primitive sur par :

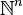
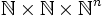
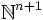
Programmation

Les fonctions récursives primitives se programment dans tout langage de programmation, à l'aide d'une simple instruction itérative for :

function f(x,y)

z := g(y)

for i from 0 to x-1 do z := h(i,z,y) od

return(z)

Il n'y a pas de boucles while et le calcul des fonctions récursives primitives se termine toujours.

Exemples

Prédécesseur d'un entier

predecesseur(0) = 0

predecesseur(Succ(x)) = x

On utilise ici la définition récursive de predecesseur en prenant n=0, g la fonction identiquement nulle, h(x,y) = x projection sur la première composante.

Somme de deux entiers

somme(0,y) = y

somme(Succ(x),y) = Succ(somme(x,y))

On utilise ici la définition récursive de somme en prenant n=1, g(y) = y, h(x,z,y) = Succ(z), composée de la fonction Successeur et de la projection sur la deuxième composante.

Somme de fonctions récursives primitives

Plus généralement, si est une fonction récursive primitive de , alors est une fonction récursive primitive de .

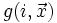
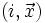
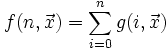
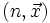
Produit de deux entiers

produit(0,y) = 0

produit(Succ(x),y) = somme(y,produit(x,y))

On utilise ici la définition récursive de produit en prenant n=1, g identiquement nulle, h(x,z,y) = somme(y,z), composée de la fonction somme déjà définie et de deux projections.

Produit de fonctions récursives primitives

Plus généralement, si est une fonction récursive primitive de , alors est une fonction récursive primitive de .

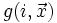
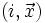
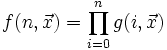
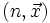
Signe d'un entier

Il s'agit de la fonction valant 0 pour x = 0 et 1 pour x > 0.

sg(0) = 0

sg(Succ(x)) = 1

On a pris n = 0, g nulle, h égale à la constante 1.

Différence tronquée

La différence tronquée de y par x vaut y-x si x < y et 0 sinon.

soustrait(0,y) = y

soustrait(Succ(x),y) = predecesseur(soustrait(x,y))

On a pris g(y) = y et pour h la fonction predecesseur déjà définie appliquée sur sa deuxième composante.

Il en résulte que la valeur absolue | x - y | = soustrait(x,y) + soustrait(y,x) est également récursive primitive.

Il en est de même de max(x,y) = x + soustrait(x,y) et de min(x,y) = soustrait(max(x,y),x+y).

Prédicats récursifs primitifs

Définition

A tout prédicat défini sur , on peut associer sa fonction caractéristique :

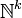
On dira que le prédicat P est récursif primitif lorsque sa fonction caractéristique est récursive primitive.

On peut montrer que, si deux prédicats P et Q sont récursifs primitifs, il en est de même des prédicats (non P), (P et Q), (P ou Q), (P implique Q).

Exemples

Le prédicat x < y est récursif primitif, puisque sa fonction caractéristique est égale à sg(soustrait(x,y)), qui est une fonction récursive primitive.

Sont également récursifs primitifs les prédicats suivants :

x divise y

x est un nombre premier

x mod y = z

Quantification bornée

Si est un prédicat récursif primitif de , alors les deux prédicats suivants sont des prédicats récursifs primitifs de  :

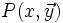
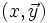
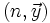
En effet, si est la fonction caractéristique associée à , alors les fonctions caractéristiques associées aux deux prédicats de quantification bornée précédents sont respectivement :

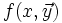
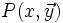
Il est très important de borner la quantification par un nombre n. En effet, les prédicats et ne sont pas récursifs primitifs.

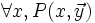
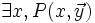
Ainsi, le prédicat "il existe un nombre parfait impair inférieur à n" est récursif primitif, mais pas le prédicat "il existe un nombre parfait impair". On ignore d'ailleurs (en 2006) la valeur de vérité de ce dernier prédicat.

Minimisation bornée

Si est un prédicat récursif primitif de , alors la fonction définie par :

le plus petit vérifiant , si un tel x existe, et = n+1 sinon

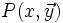
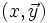
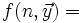
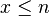
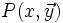
est récursive primitive.

En effet, si est la fonction caractéristique associée à , alors f est définie comme suit :

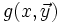
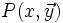
Là aussi, il est important de borner la recherche du minimum. La fonction cherchant le plus petit x vérifiant n'est plus récursive primitive en général.

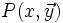
Ainsi, la fonction cherchant le plus petit nombre parfait impair inférieur à n (ou n+1 s'il n'existe pas) est une fonction récursive primitive de n. Mais la fonction donnant le plus petit nombre parfait impair n'est pas récursive primitive.

Limites de la récursion primitive

Une première limitation de la récursion primitive intervient dans les algorithmes susceptibles de ne pas se terminer. Tel est le cas de la quantification non bornée ou de la minimisation non bornée, vues précédemment.

Mais il ne suffit qu'une fonction soit définie récursivement, et par un procédé se terminant pour toute valeur des données, pour que la fonction soit récursive primitive. L'ensemble des fonctions récursives primitives n'est en effet qu'une partie de l'ensemble des fonctions récursives. Ainsi, la fonction d'Ackermann définie par

ackermann(0,p) = Succ(p)

ackermann(Succ(n),0) = ackermann(n,1)

ackermann(Succ(n),Succ(p)) = ackermann(n,ackermann(Succ(n),p))

n'est pas récursive primitive car la récursion se fait sur deux entiers simultanément. Pourtant la définition doublement récursive de cette fonction permet en théorie de calculer sa valeur pour tout couple (n,p) d'entiers.

Le même problème se pose si on veut utiliser cet algorithme du minimum :

minimum(0,p) = 0

minimum(Succ(n),0) = 0

minimum(Succ(n),Succ(p)) = Succ(minimum(n,p))

Bien que la fonction minimum soit récursive primitive, ce n'est pas la définition précédente qui permet de le montrer.

Pour pouvoir réaliser ces programmes on doit passer un système plus puissant, comme le Système T de Gödel par exemple.

Un problème indécidable

Indécidabilité de la récursion primitive

Nous avons vu, dans le paragraphe Limites de la récursion primitive, deux exemples de définitions récursives qui ne sont pas récursives primitives :

• La fonction d'Ackermann, dont on peut montrer qu'elle n'est pas récursive primitive. Il n'existe aucune définition de la fonction d'Ackermann utilisant la récursion primitive.
• La fonction minimum, qui, elle, est cependant récursive primitive. Il existe une autre définition de la fonction minimum n'utilisant que la récursion primitive (cf Exemples/Différence tronquée).

Se pose alors la question suivante. Etant donnée une fonction, définie récursivement ou par un algorithme quelconque, est-il possible de déterminer par un processus automatique si cette fonction est récursive primitive ? Est-il possible de savoir si sa définition peut être modifiée pour ne faire appel qu'à la récursion primitive ? La réponse à cette question est négative. Il n'existe aucune procédure permettant de dire si une fonction est récursive primitive ou non. On dit que la détermination du caractère récursif primitif d'une fonction définie par un algorithme est indécidable. C'est un cas particulier du théorème de Rice, qui définit toute une classe de questions indécidables.

Démonstration

Nous pouvons donner schématiquement le raisonnement conduisant à cette conclusion. Les fonctions définies par un algorithme peuvent être numérotées par ordre croissant, au moyen d'un codage numérique de l'algorithme ou de la machine de Turing qui les définit. On appellera φ_n la n-ème fonction ainsi définie.

Raisonnons par l'absurde et supposons qu'il existe une procédure RP s'appliquant à l'algorithme définissant une fonction f (ou à l'entier n tel que f = φ_n) et qui vaut 1 si f est récursive primitive et 0 sinon. Notons RP(f) cette valeur 0 ou 1. Considérons alors, pour chaque entier n la fonction g_n de x définie par :

Si l'algorithme de la fonction φ_n se termine par une valeur quelconque lorsqu'on l'applique à l'entier n lui-même, alors g_n est identiquement nulle. Elle est alors récursive primitive, et RP(g_n) = 1. Par contre, si l'algorithme de la fonction φ_n se met à boucler indéfiniment lorsqu'on l'applique à l'entier n lui-même, alors le calcul de g_n(x) ne se termine pas. g_n n'est pas récursive primitive, et RP(g_n) = 0. On a donc :

RP(g_n) = 0 si et seulement si le calcul de φ_n(n) ne se termine pas.

Considérons enfin la fonction C définie par l'algorithme suivant :

function C(n)

if RP(g_n) = 0

then return(0)

else while true do od

if

La fonction C fonctionne comme suit : si RP(g_n) = 0, alors C(n) retourne la valeur 0. Mais si RP(g_n) = 1, alors C(n) entre dans une boucle dont elle ne ressort pas, et l'algorithme ne se termine pas. Autrement dit :

Le calcul de C(n) se termine si et seulement si RP(g_n) = 0, si et seulement si le calcul de φ_n(n) ne se termine pas.

C étant défini par algorithme possède un rang c tel que C = φ_c. L'équivalence ci-dessus s'écrit alors :

Le calcul de φ_c(n) se termine si et seulement si le calcul de φ_n(n) ne se termine pas.

Que se passe-t-il lorsqu'on donne à n la valeur c ? L'équivalence devient :

Le calcul de φ_c(c) se termine si et seulement si le calcul de φ_c(c) ne se termine pas.

ce qui est absurde.

Aboutissant à une contradiction, on en conclut que la procédure RP ne peut exister.

Exemple

Considérons la fonction définie comme suit, pour n>0 :

function Collatz(n)

while n<>1 do

if n mod 2 = 0 then n := n/2

else n := 3*n+1 fi

od

return(1)

On ignore si, pour tout n, la boucle while se termine ou si, au contraire, il existe un entier n pour lequel le programme boucle indéfiniment. La conjecture de Syracuse postule que c'est le premier cas qui se produit. Il en résulterait alors que la fonction Collatz est la fonction constante égale à 1, et donc récursive primitive. Mais on est actuellement dans l'incapacité de prouver cette assertion.

Formalismes

La récursion primitive est un langage de programmation théorique qui a la propriété que tous les programmes écrits dans ce langage terminent. Pour pouvoir écrire des programmes dans ce langage on peut utiliser différents formalismes.

Les termes de Martin-Löf

Les termes de Martin-Löf sont soit :

• le numéral 0
• le successeur d'un terme Succ
• une variable a, b, c, ...
• une récursion : Rec(t, b, (x,y) s)

Dans la récursion, t est un terme sur lequel on fait la récursion, b est le cas de base et s l'étape de récurrence. Dans l'étape de récurrence, la variable x représente le prédécesseur de l'entier sur lequel on fait la récurrence et le y est l'étape de récurrence.

Sémantique

Exemple

L'addition de n et p s'écrit Rec(n,p,(x,y)Succ(y)).

Les Combinateurs de Kleene

Kleene a introduit les combinateurs qui sont une autre manière de représenter les fonctions récursives primitives. Les combinateurs sont munis d'arité, c'est-à-dire qu'ils ont un nombre de paramètres défini (sauf dans un cas particulier).

Un combinateur est :

• le combinateur 0 d'arité zéro. C'est une fonction constante.
• le combinateur Succ d'arité un qui va associer à un combinateur son successeur
• la i^e projection : π_iⁿ d'arité n qui va associer à un n-uplet le i^e élément.
• l'application S(c;c₁, ..., c_n), c étant un combinateur d'arité n, et les c_i des combinateurs d'arité m et le combinateur en entier est d'arité m. Ce combinateur sert à donner à un combinateur des paramètres quelconques.
• la Récursion : Rec(b,s) avec b un combinateur d'arité n, s un combinateur d'arité n+2 et le combinateur en entier est d'arité n+1. b est le cas de base et s l'étape de récurrence.

Sémantique

Exemples

L'addition se programme ainsi : Rec(π₁¹, S(Succ,π₂³))