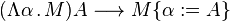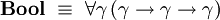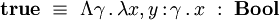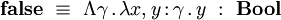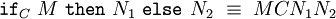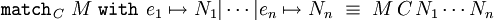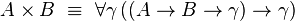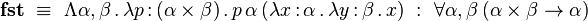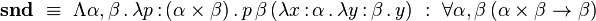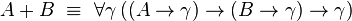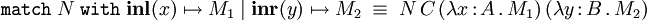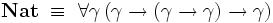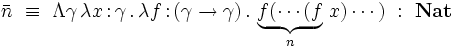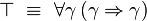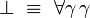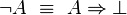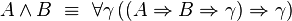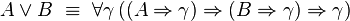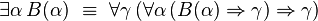Système F - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Le système F (également connu sous le nom de lambda-calcul polymorphe ou de lambda-calcul du second ordre) est une extension du lambda-calcul simplement typé introduite indépendamment par le logicien Jean-Yves Girard et par l'informaticien John C. Reynolds. Ce système se distingue du lambda-calcul simplement typé par l'introduction d'un mécanisme de quantification universelle de type qui permet d'exprimer le polymorphisme paramétrique.

Ainsi que l'atteste sa double origine, le système F peut être étudié dans deux contextes très différents:

Dans le domaine de la programmation fonctionnelle, où il apparaît comme une extension très expressive du noyau du langage ML. Son expressivité est illustrée par le fait que les types de données courants (booléens, entiers, listes, etc.) sont définissables dans le système F à partir des constructions de base.

Dans le domaine de la logique, et plus particulièrement de la théorie de la démonstration. À travers la correspondance de Curry-Howard, le système F est en effet isomorphe à la logique minimale intuitionniste du second ordre. En outre, ce système capture très exactement la classe des fonctions numériques dont l'existence est prouvable en arithmétique intuitionniste du second ordre (parfois appelée analyse intuitionniste). C'est d'ailleurs cette propriété remarquable du système F qui a historiquement motivé son introduction par Jean-Yves Girard, dans la mesure où cette propriété permet de résoudre le problème de l'élimination des coupures en arithmétique du second ordre, conjecturé par Takeuti.

Comme le lambda-calcul simplement typé, le système F admet deux présentations équivalentes:

Une présentation à la Church, dans laquelle chaque terme contient toutes les annotations de type nécessaires à la reconstruction de son type (de manière univoque).

Une présentation à la Curry, due à l'informaticien Daniel Leivant, dans laquelle les termes (qui sont ceux du lambda-calcul pur) sont dépourvus de toute annotation de type, et sont ainsi sujets aux problèmes d'ambiguïté typique.

Présentation à la Church

La syntaxe

Les types du système F (notés $A$ , $B$ , $C$ , etc.) sont formés à partir d'un ensemble de variables de types (notées $α$ , $β$ , $γ$ , etc.) à l'aide des trois règles de construction suivantes:

(Variable de type) Si $α$ est une variable de type, alors $α$ est un type;
(Type flèche) Si $A$ et $B$ sont des types, alors $A\to B$ est un type;
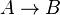
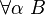
(Type universel) Si $α$ est une variable de type et $B$ un type, alors $\forall\alpha~B$ est un type.

En résumé, les types du système F sont donnés par la grammaire BNF:

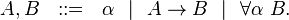
$A,B ~~::=~~ \alpha ~~|~~ A\to B ~~|~~ \forall\alpha~B.$

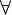
Comme en lambda-calcul ou en calcul des prédicats, la présence d'un symbole mutificateur $\forall$ nécessite de distinguer les notions de variable libre et de variable liée, et d'introduire les mécanismes usuels de renommage permettant de travailler à $α$ -conversion près. Enfin, l'algèbre de types du système F est munie d'une opération de substitution similaire à celle du lambda-calcul, et l'on note $B {α: = A}$ le type obtenu en remplaçant dans le type $B$ toutes les occurrences libres de la variable de type $α$ par le type $A$ .

Les termes (bruts) du système F (notés $M$ , $N$ , etc.) sont formés à partir d'un ensemble de variables de termes (notées $x$ , $y$ , $z$ , etc.) à l'aide des cinq règles de construction suivantes:

(Variable) Si $x$ est une variable de terme, alors $x$ est un terme;
(Abstraction) Si $x$ est une variable de terme, $A$ un type et $M$ un terme, alors $λ x : A . M$ est un terme;
(Application) Si $M$ et $N$ sont des termes, alors $M N$ est un terme;
(Abstraction de type) Si $α$ est une variable de type et $M$ un terme, alors $Λα. M$ est un terme;
(Application de type) Si $M$ est un terme et $A$ un type, alors $M A$ est un terme.

En résumé, les termes (bruts) du système F sont donnés par la grammaire BNF:

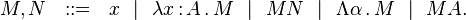
$M,N ~~::=~~ x ~~|~~ \lambda x\,{:}\,A\,.\,M ~~|~~ MN ~~|~~ \Lambda\alpha\,.\,M ~~|~~ MA.$

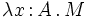
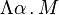
On notera que les termes du système F incorporent deux mécanismes de liaison de variable: un mécanisme de liaison de variables de termes (par la construction $\lambda x\,{:}\,A\,.\,M$ ) et un mécanisme de liaison de variables de types (par la construction $\Lambda\alpha\,.\,M$ ), qui sont tous les deux pris en compte au niveau de la relation d' $α$ -conversion. Ce double mécanisme donne naturellement lieu à deux opérations de substitution: une substitution de terme notée $M {x : = N}$ , et une substitution de type notée $M {α: = A}$ .

La $β$ -réduction

La présence d'un double mécanisme d'abstraction et d'application (abstraction/application de terme et abstraction/application de type) donne lieu à deux règles de $β$ -réduction, dont l'union engendre par passage au contexte la relation de $β$ -réduction en une étape du système F:

$(\lambda x\,{:}\,A\,.\,M)N\longrightarrow M\{x:=N\}$
$(\Lambda\alpha\,.\,M)A\longrightarrow M\{\alpha:=A\}$

Comme pour le lambda-calcul pur, la $β$ -réduction du système F est confluente (sur les termes bruts) et vérifie la propriété de Church-Rosser:

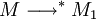
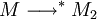
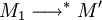
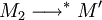
(Confluence de la $β$ -réduction) Si $M\longrightarrow^*M_1$ et $M\longrightarrow^*M_2$ , alors il existe un terme $M'$ tel que $M_1\longrightarrow^*M'$ et $M_2\longrightarrow^*M'$ .
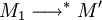
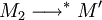
(Propriété de Church-Rosser) Pour que deux termes $M 1$ et $M 2$ soient $β$ -convertibles, il faut et il suffit qu'il existe un terme $M'$ tel que $M_1\longrightarrow^*M'$ et $M_2\longrightarrow^*M'$ .

Le système de types

On appelle contexte de typage (notation: $Γ$ , $Γ'$ , etc.) toute liste finie de déclarations de la forme $x : A$ (où $x$ est une variable de terme et $A$ un type) dans laquelle une variable de terme est déclarée au plus une fois.

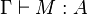
Le système de types du système F est construit autour d'un jugement de typage de la forme $\Gamma\vdash M:A$ (" dans le contexte $Γ$ , le terme $M$ a pour type $A$ "), qui est défini à partir des règles d'inférence suivantes:

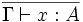
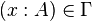
(Axiome) $\frac{}{\Gamma\vdash x:A}$ si $(x:A)\in\Gamma$

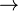
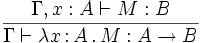
( $\to$ -intro) $\frac{\Gamma,x:A\vdash M:B}{\Gamma\vdash\lambda x\,{:}\,A\,.\,M:A\to B}$

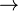
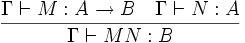
( $\to$ -élim) $\frac{\Gamma\vdash M:A\to B\quad\Gamma\vdash N:A}{\Gamma\vdash MN:B}$

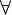
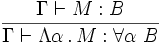
( $\forall$ -intro) $\frac{\Gamma\vdash M:B}{\Gamma\vdash\Lambda\alpha\,.\,M:\forall\alpha~B}$ si $α$ n'a pas d'occurrence libre dans $Γ$

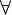
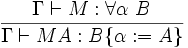
( $\forall$ -élim) $\frac{\Gamma\vdash M:\forall\alpha~B}{\Gamma\vdash MA:B\{\alpha:=A\}}$ .

Les deux propriétés principales de ce système de types sont la propriété de préservation du type par $β$ -réduction et la propriété de normalisation forte:

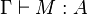
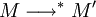
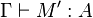
(Préservation du type par réduction) Si $\Gamma\vdash M:A$ et si $M\longrightarrow^*M'$ , alors $\Gamma\vdash M':A$ .

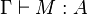
(Normalisation forte) Si $\Gamma\vdash M:A$ , alors $M$ est fortement normalisable.

La première de ces deux propriétés est une propriété purement combinatoire qui se démontre par une induction directe sur la dérivation de typage. En revanche, la propriété de normalisation forte du système F est une propriété dont la démonstration repose fondamentalement sur des méthodes non-combinatoires, basées sur la notion de candidat de réductibilité.

Représentation des types de données

Pour pouvoir utiliser le lambda-calcul simplement typé comme un langage de programmation, il est nécessaire de lui adjoindre des types de base (booléens, entiers, etc.) et des règles de réduction supplémentaires qui étendent le pouvoir expressif du formalisme. Un exemple d'une telle extension est le système T de Gödel, qui est obtenu en ajoutant au lambda-calcul simplement typé des entiers naturels primitifs et un mécanisme de récursion similaire à la récursion primitive (mais plus expressif).

Dans le système F, une telle extension n'est pas nécessaire car l'expressivité du formalisme permet de définir les types de base et les constructeurs de types usuels sans qu'il soit nécessaire de modifier ni le système de types ni les règles de réduction.

Booléens et types finis

Le type des booléens est défini dans le système F par

$\textbf{Bool}~\equiv~\forall\gamma\,(\gamma\to\gamma\to\gamma)$

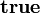
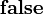
et les constantes $\textbf{true}$ et $\textbf{false}$ par:

$\textbf{true}~\equiv~\Lambda\gamma\,.\,\lambda x,y\,{:}\,\gamma\,.\,x~:~\textbf{Bool}$
$\textbf{false}~\equiv~\Lambda\gamma\,.\,\lambda x,y\,{:}\,\gamma\,.\,y~:~\textbf{Bool}$

On peut démontrer que les deux termes ci-dessus sont les deux seuls termes clos en forme normale de type . Ainsi, le type de données capture effectivement la notion de booléen.

La construction 'if ... then ... else ...' est définie par

$\texttt{if}_C~M~\texttt{then}~N_1~\texttt{else}~N_2~\equiv~MCN_1N_2$

où $C$ désigne le type d'élimination de la construction 'if ...', c'est-à-dire le type commun aux deux branches de la conditionnelle. Cette définition est correcte du point de vue du typage comme du point de vue calculatoire dans la mesure où:

Dans tout contexte où le terme $M$ a le type et où les termes $N 1$ et $N 2$ ont le type $C$ , la construction est bien typée et a pour type le type $C$ .

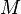
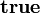
Si le terme $M\,\!$ se réduit sur $\textbf{true}$ , alors la construction se réduit sur $N_1\,\!$ .
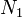
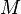
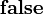
Si le terme $M\,\!$ se réduit sur $\textbf{false}$ , alors la construction se réduit sur $N_2\,\!$ .

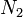
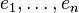
Plus généralement, on peut définir un type fini $E n$ à $n$ valeurs $e_1,\ldots,e_n$ en posant

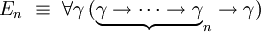
$E_n~\equiv~\forall\gamma\,(\underbrace{\gamma\to\cdots\to\gamma}_n\to\gamma)$
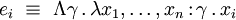
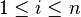
$e_i~\equiv~\Lambda\gamma\,.\,\lambda x_1,\ldots,x_n\,{:}\,\gamma\,.\,x_i$ (pour tout $1\le i\le n$ )

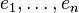
Là encore, on peut démontrer que les termes $e_1,\ldots,e_n$ sont les seuls termes clos en forme normale de type $E n$ . L'opération de filtrage correspondant est définie par:

$\texttt{match}_C~M~\texttt{with}~e_1\mapsto N_1|\cdots|e_n\mapsto N_n~\equiv~M\,C\,N_1\cdots N_n$

(où $C$ désigne le type des branches de filtrage).

En particulier:

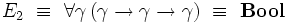
$E_2~\equiv~\forall\gamma\,(\gamma\to\gamma\to\gamma)~\equiv~\textbf{Bool}$ (type des booléens)
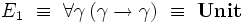
$E_1~\equiv~\forall\gamma\,(\gamma\to\gamma)~\equiv~\textbf{Unit}$ (type singleton)
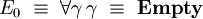
$E_0~\equiv~\forall\gamma\,\gamma~\equiv~\textbf{Empty}$ (type vide)

On notera que le type $E 0$ n'est habité par aucun terme clos en forme normale, et, d'après le théorème de normalisation forte, qu'il n'est habité par aucun terme clos.

Produit cartésien et somme directe

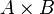
Soit $A$ et $B$ deux types. Le produit cartésien $A\times B$ est défini dans le système F par

$A\times B~\equiv~\forall\gamma\,((A\to B\to\gamma)\to\gamma)$

et la construction de couple par

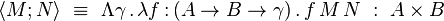
$\langle M;N\rangle~\equiv~\Lambda\gamma\,.\,\lambda f\,{:}\,(A\to B\to\gamma)\,.\,f\,M\,N~:~A\times B$ (si $M:A\,\!$ et $N:B\,\!$ )

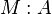
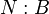
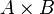
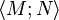
Comme pour les types énumérés, on peut démontrer que les seuls termes clos en forme normale de type $A\times B$ sont de la forme $\langle M;N\rangle$ , où $M$ et $N$ sont des termes clos en forme normale de type $A$ et $B$ , respectivement. Les fonctions de projection correspondantes sont données par

$\textbf{fst}~\equiv~\Lambda\alpha,\beta\,.\,\lambda p\,{:}\,(\alpha\times\beta)\,.\,p\,\alpha\,(\lambda x\,{:}\,\alpha\,.\,\lambda y\,{:}\,\beta\,.\,x)~:~\forall\alpha,\beta\,(\alpha\times\beta\to\alpha)$
$\textbf{snd}~\equiv~\Lambda\alpha,\beta\,.\,\lambda p\,{:}\,(\alpha\times\beta)\,.\,p\,\beta\,(\lambda x\,{:}\,\alpha\,.\,\lambda y\,{:}\,\beta\,.\,y)~:~\forall\alpha,\beta\,(\alpha\times\beta\to\beta)$

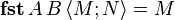
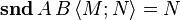
Ces fonctions vérifient naturellement les égalités $\textbf{fst}\,A\,B\,\langle M;N\rangle=M$ et $\textbf{snd}\,A\,B\,\langle M;N\rangle=N$ .

La somme directe $A + B$ est définie par

$A+B~\equiv~\forall\gamma\,((A\to\gamma)\to(B\to\gamma)\to\gamma)$

Les habitants des types $A$ et $B$ sont plongés dans le type $A + B$ à l'aide des constructions

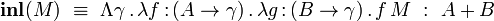
$\textbf{inl}(M)~\equiv~\Lambda\gamma\,.\,\lambda f\,{:}\,(A\to\gamma)\,.\,\lambda g\,{:}\,(B\to\gamma)\,.\,f\,M~:~A+B$ (si $M:A\,\!$ )
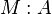
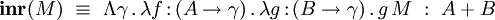
$\textbf{inr}(M)~\equiv~\Lambda\gamma\,.\,\lambda f\,{:}\,(A\to\gamma)\,.\,\lambda g\,{:}\,(B\to\gamma)\,.\,g\,M~:~A+B$ (si $M:B\,\!$ )

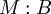
tandis que le filtrage des éléments de type $A + B$ est assuré par la construction

$\texttt{match}~N~\texttt{with}~\textbf{inl}(x)\mapsto M_1~|~\textbf{inr}(y)\mapsto M_2~\equiv~N\,C\,(\lambda x\,{:}\,A\,.\,M_1)\,(\lambda y\,{:}\,B\,.\,M_2)$

qui satisfait les égalités définitionnelles attendues.

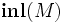
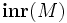
Contrairement au produit cartésien, l'encodage de la somme directe dans le système F ne capture pas toujours la notion d'union disjointe, dans la mesure où il est possible, dans certains cas, de construire des termes clos en forme normale de type $A + B$ qui ne sont ni de la forme $\textbf{inl}(M)$ (avec $M : A$ ) ni de la forme $\textbf{inr}(M)$ (avec $M : B$ ).

Les entiers de Church

Le type des entiers de Church est défini dans le système F par

$\mathbf{Nat}~\equiv~\forall\gamma\,(\gamma\to(\gamma\to\gamma)\to\gamma)$

Chaque entier naturel $n$ est représenté par le terme

$\bar{n}~\equiv~\Lambda\gamma\,\lambda x\,{:}\,\gamma\,.\,\lambda f\,{:}\,(\gamma\to\gamma)\,.\,\underbrace{f(\cdots(f}_n\,x)\cdots)~:~\mathbf{Nat}$

Comme pour les booléens, le type $\mathbf{Nat}$ capture la notion d'entier naturel puisque tout terme clos de type $\mathbf{Nat}$ en forme normale est de la forme $\bar{n}$ pour un certain entier naturel $n$ .

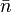
Présentation à la Curry

La fonction d'effacement

$| x | = x$
$| λ x : A . M | = λ x . | M |$
$| M N | = | M | | N |$
$| Λα. M | = | M |$
$| M A | = | M |$

Le système de types

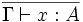
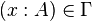
(Axiome) $\frac{}{\Gamma\vdash x:A}$ si $(x:A)\in\Gamma$

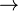
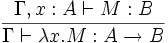
( $\to$ -intro) $\frac{\Gamma,x:A\vdash M:B}{\Gamma\vdash\lambda x.M:A\to B}$

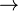
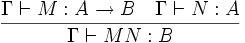
( $\to$ -élim) $\frac{\Gamma\vdash M:A\to B\quad\Gamma\vdash N:A}{\Gamma\vdash MN:B}$

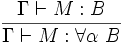
( $\forall$ -intro) $\frac{\Gamma\vdash M:B}{\Gamma\vdash M:\forall\alpha~B}$ si $α$ n'a pas d'occurrence libre dans $Γ$

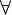
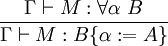
( $\forall$ -élim) $\frac{\Gamma\vdash M:\forall\alpha~B}{\Gamma\vdash M:B\{\alpha:=A\}}$ .

Équivalence entre les deux systèmes

Le théorème de normalisation forte

Les termes typables du système F sont fortement normalisables.

Correspondance avec la logique du second ordre

À travers la correspondance de Curry-Howard, le système F correspond très exactement à la logique minimale intuitionniste du second ordre, dont les formules sont construites à partir des variables propositionnelles à l'aide de l'implication et de la quantification propositionnelle:

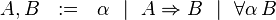
$A,B ~~:=~~ \alpha ~~|~~ A\Rightarrow B ~~|~~ \forall\alpha\,B$

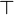
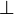
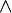
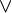
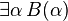
Rappelons que dans ce cadre, les unités $\top$ (vérité) et $\bot$ (absurdité), les connecteurs $\lnot$ (négation), $\land$ (conjonction) et $\lor$ (disjonction) et la quantification existentielle $\exists\alpha\,B(\alpha)$ sont définissables par

$\top~\equiv~\forall\gamma\,(\gamma\Rightarrow\gamma)$
$\bot~\equiv~\forall\gamma\,\gamma$
$\lnot A~\equiv~A\Rightarrow\bot$
$A\land B~\equiv~\forall\gamma\,((A\Rightarrow B\Rightarrow\gamma)\Rightarrow\gamma)$
$A\lor B~\equiv~\forall\gamma\,((A\Rightarrow\gamma)\Rightarrow(B\Rightarrow\gamma)\Rightarrow\gamma)$
$\exists\alpha\,B(\alpha)~\equiv~\forall\gamma\,(\forall\alpha\,(B(\alpha)\Rightarrow\gamma)\Rightarrow\gamma)$

(On notera qu'à travers la correspondance de Curry-Howard, l'absurdité correspond au type vide, la vérité au type singleton, la conjonction au produit cartésien et la disjonction à la somme directe.)

On démontre que dans ce formalisme, une formule est prouvable sans hypothèses si et seulement si le type correspondant dans le système F est habité par un terme clos.

Correspondance avec l'arithmétique du second ordre

Bibliographie

Lambda-calcul, types et modèles, Jean-Louis Krivine, chapitre VIII, Masson, 1990, ISBN 2225820910
Proofs and Types, Jean-Yves Girard, Paul Taylor, Yves Lafont, chapitre 11, Cambridge University Press, 1989, ISBN 0521371813

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Page générée en 0.180 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise

Système F - Définition

Présentation à la Church

La syntaxe

La β-réduction

Le système de types

Représentation des types de données

Booléens et types finis

Produit cartésien et somme directe

Les entiers de Church

Présentation à la Curry

La fonction d'effacement

Le système de types

Équivalence entre les deux systèmes

Le théorème de normalisation forte

Correspondance avec la logique du second ordre

Correspondance avec l'arithmétique du second ordre

Bibliographie

La $β$ -réduction