Pierre de Fermat - Définition
Pierre de Fermat, né le 20 août 1601, à Beaumont-de-Lomagne, près de Montauban, et décédé le 12 janvier 1665 à Castres, était un juriste et mathématicien français, surnommé " le prince des amateurs ".
Biographie
Son père, Dominique Fermat, était un marchand aisé, bourgeois et second consul de la ville comme marchand de cuir et autres denrées. Il a été éduqué à la maison par sa mère, Claire Delong, professeur de mathématiques. Par la suite, il fait des études de droit à Toulouse, Bordeaux et Orléans. Dès 1631, il achète une charge de conseiller du roi à la Chambre des Requêtes du Parlement de Toulouse. Avec fidélité et assurance dans cet emploi de magistrat, il remplit sa tâche et grimpe rapidement les échelons vers un emploi de notable à la Chambre Criminelle et la Grand’ Chambre et enfin, membre de la chambre de l'édit de Castres (1648). C'est à ce dernier poste qu'une particule de noblesse s'ajoute à son nom et il se nomme dorénavant Pierre de Fermat.
Ses talents de mathématiciens se sont exercés à part de son travail de magistrat puisque les seuls grands écrits que l'on ait retrouvés de lui sont des annotations dans des textes renommés tels l'Arithmetica de Diophante.
À ses amis mathématiciens (Descartes, Pascal, Roberval, Torricelli, Huygens, Mersenne), il demande de démontrer par la preuve les théories qu'il avance ce qui ravive l'ire des autres envers lui. En 1652, la fameuse peste qui ravage la France s'attaquera à lui mais il y fera face et la combattra. Ce n'est qu'en 1670 que son théorème est exposé au public et l'on devra attendre jusqu'au 19 septembre 1994 pour qu'il soit prouvé par le mathématicien anglais Andrew Wiles.
Il s'est aussi intéressé aux sciences physiques ; on lui doit notamment le Principe de Fermat en optique.
Contributions
Il partage avec Descartes la gloire d'avoir appliqué l'algèbre à la géométrie. Il imagina pour la solution des problèmes, une méthode, dite de maximis et minimis, qui le fait regarder comme le premier inventeur du calcul différentiel dont il est un précurseur : il est le premier à utiliser la formule (sinon le concept) du nombre dérivé.
Il pose en même temps que Blaise Pascal les bases du calcul des probabilités. Mais sa contribution majeure concerne la théorie des nombres et les équations diophantiennes. Auteur de plusieurs théorèmes ou conjectures dans ce domaine, il est au cœur de la " théorie moderne des nombres ".
Il est très connu pour deux " théorèmes " :
- le " petit théorème de Fermat " ;
- le " dernier théorème de Fermat " ; ce dernier n'était qu'une conjecture et l'est resté durant près de quatre siècles de recherches fiévreuses.
Petit théorème de Fermat
Si p est un nombre premier et a un entier naturel non divisible par p, alors
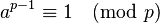
Voir aussi : Théorème d'Euler, Dont ce théorème est un cas particulier.
Théorème des deux carrés de Fermat
Pour qu'un nombre premier impair soit la somme de deux carrés, il faut et il suffit qu'il soit congru à 1 modulo 4.
Théorème de Fermat sur les nombres polygonaux
Tout entier s'écrit :
- comme somme d'au plus 3 nombres triangulaires
- comme somme d'au plus 4 nombres carrés
- comme somme d'au plus 5 nombres pentagonaux
- etc.
- nombres triangulaires :
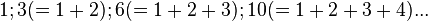
- nombres carrés :
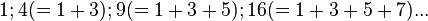
- nombres pentagonaux :
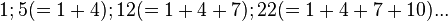
- nombres polygonaux d'ordre m :
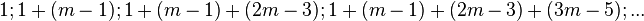
- nombres triangulaires :
Ce théorème a été énoncé par Fermat, démontré dans le cas des nombres carrés par Jacobi et, indépendamment par Joseph-Louis Lagrange au XVIIIe siècle (Ce dernier se servant de résultats partiels obtenus par Euler). Gauss résolut le cas des nombres triangulaires en 1796. Une preuve complète a été proposée par Cauchy en 1813.
Grand théorème de Fermat (ou Dernier théorème de Fermat)
Il n'existe pas d'entiers strictement positifs
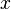
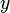
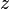
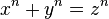
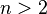
Ce théorème fut démontré par le mathématicien anglais Andrew Wiles de l'Université de Princeton, avec l'aide de Richard Taylor. Après une première présentation en juin 1993, puis la découverte d'une erreur et un an de travaux supplémentaires, la preuve fut finalement publiée en 1995 dans Annals of Mathematics.
Pierre de Fermat lui-même annotait en marge de son exemplaire des Arithmétiques qu’il en avait découvert une démonstration vraiment remarquable, mais manquait de place pour la donner à cet endroit:"j'ai découvert une preuve réellement remarquable que cette marge trop étroite ne me permet pas de détailler".
La démonstration évoquée par Pierre de Fermat est soit fausse, soit inconnue à ce jour, car la démonstration réalisée par Andrew Wiles utilise des outils mathématiques dont M. de Fermat ne pouvait vraisemblablement disposer compte tenu des connaissances de son époque.
Méthode de la descente infinie
Fermat est par ailleurs l'inventeur d'une méthode de démonstration, la descente infinie. Elle consiste à démontrer que si une proposition P est vraie à un rang r, elle l'est à un rang q inférieur à r. Si on aboutit à une contradiction, on démontre alors que P est fausse. Cette méthode très astucieuse a été utilisée par Fermat pour démontrer son grand théorème dans le cas particulier n = 4.
Principe de Fermat (optique)
Le trajet parcouru par la lumière entre deux points est toujours celui qui minimise le temps de parcours. Voir l'article principe de Fermat
Œuvres
Il commenta, en l'étendant, Diophante, et rétablit avec une admirable sagacité plusieurs ouvrages perdus d'Apollonius et d'Euclide. Il était en même temps un habile helléniste et un profond jurisconsulte. Ce savant cachait ses méthodes, dont quelques-unes ont été perdues avec lui.
On a de lui quelques opuscules, publiés 15 ans après sa mort par son fils, Samuel de Fermat, sous le titre de Varia opera mathematica, Toulouse, 1679, et des Remarques sur Diophante, dans l'édition de cet auteur donnée en 1670.

















































