Algèbre d'un groupe fini - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Représentation régulière
On suppose dans ce paragraphe que la caractéristique de K est soit nulle soit première avec g et K est alors algébrique. On suppose de plus que le polynôme Xg - 1 est scindé.
La représentation régulière correspond à celle de l'algèbre de groupe. Par défaut, elle ne dispose pas d'une multiplication interne mais d'un morphisme de groupe de G dans le groupe linéaire de l'espace vectoriel V de dimension g. Une analyse de la représentation apporte un éclairage important sur K[G]. En particulier, on démontre que toutes les représentations irréductibles sont isomorphes à un G-module, et plus précisément :
-
- Soient (V, ρ) la représentation régulière de G et (W, σ) une représentation irréductible de G de degré d, il existe exactement d sous espaces invariants Vi de V, d'intersection nulle deux à deux, tel que la restriction ρi de ρ à Vi soit une représentation isomorphe à (W, σ).
La démonstration est donnée dans l'article associé.
L'analyse de l'algèbre du groupe permet de comprendre plus profondément la structure de la représentation régulière. Une définition est néanmoins nécessaire :
-
- Un espace somme directe de copies d'un G-module simple est dit isotypique. La somme directe de toutes les copie d'un G-module simple est appelée composante isotypique du module simple dans le G-module.
La représentation régulière, isomorphe à K[G] est un module semi-simple de longueur fini. K[G] est donc somme directe d'un nombre fini de sous-modules, correspondant à des représentations irréductibles. Soit (Si) une famille maximale de sous-modules non isomorphes deux à deux. Cette famille est finie et l'on note h son cardinal. La théorie des modules semi-simples indique que la composante isotypique de Si ne contient que des représentations irréductibles isomorphes à Si. Si di est le nombre de copies de Si contenues dans une somme directe égal à la composante isotypique, alors celle-ci est notée
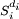
![\mathbb K[G] \; \simeq \; \bigoplus_{i=1}^h S_i^{d_i}](https://static.techno-science.net/illustration/Definitions/autres/4/43f1eb7861b0144f5393c05391014a71_657ac7a06b209876910ad523fb823a54.png)
La démonstration est donnée dans l'article Module semi-simple.
Théorème d'Artin-Wedderburn
Avec les notations du paragraphe précédent, le théorème d'Artin-Wedderburn indique que :
-
- Il existe un isomorphisme d'algèbres entre K[G] et la somme directe des h algèbres LK(Si) des endomorphismes de Vi en tant qu'espaces vectoriels sur K.
![\mathbb K[G] \; \simeq \; \bigoplus_{i=1}^h \mathcal L_{\mathbb K}(S_i)](https://static.techno-science.net/illustration/Definitions/autres/d/d6ebf29468aef10e820deae456b0bbef_ed390ec48127e3c2c00b47654ad1872e.png)
Cet isomorphisme montre par exemple que si (di) est la famille du paragraphe précédent, c'est aussi la dimension de Si, on retrouve l'égalité suivante :
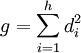
Il est toute fois possible de déterminer l'isomorphisme directement, sans utiliser le théorème. La démonstration est donnée dans la boîte déroulante.
Construction de l'isomorphisme :
Soit k un entier entre 1 et h et ψk une représentation irréductible de Sk, c’est-à-dire un morphisme de groupe entre G et GL(Sk). Soit φk le prolongement de ψk par linéarité à K[G] dans L(k) et enfin φ l'application de K[G] dans la somme directe des L(Si) qui à x associe le produit des φi(x) pour i variant de 1 à h. L'application φ est un morphisme d'algèbre, montrons qu'il est bijectif.
Surjectivité :
Il suffit de montrer que φk est surjectif si k est un entier entre 1 et h. Soit (fnmk) la matrice de φk dans une base quelconque de Sk. Montrer que φk est surjectif revient à montrer que si s décrit le groupe G, alors φk(s) est une famille génératrice de L(Sk). L'espace généré par les φk(s) est de dimension celle de la famille des fonctions de KG qui à s associe fnmk(s) correspondant à dk au carré coefficients de la représentation matricielle. Or le lemme de Schur (cf corolaire 4) montre la relation suivante :
![\forall n,m,n',m' \in [1,d] \quad \frac{1}{g}\sum_{s\in G} f_{nm}^k(s). f_{n'm'}^k(s^{-1}) = \frac{1}{d}\delta_{nm'}\delta_{n'm}](https://static.techno-science.net/illustration/Definitions/autres/c/ca7542c57c51048979ce5b4ca3711417_7286777be5acc684a174cd5ca760dbb8.png)
Ce qui exprime l'orthogonalité des différents coefficients pour une forme bilinéaire. La famille des coefficients est libre, donc de rang le carré de d k si ce nombre désigne ici la dimension de Sk. La famille φk(s) est donc de rang la dimension de L(Sk), ce qui montre la surjectivité.
Injectivité :
Les dimensions de K[G] et du produits d'algèbres d'endomorphismes sont les mêmes et φ est surjective, ce qui démontre l'injectivité.Centre de l'algèbre
Un anneau important de l'algèbre de groupe est le centre D de K[G], c’est-à-dire l'ensemble des éléments commutant avec tous les éléments de l'algèbre. La théorie des algèbres semi-simples indique que c'est un anneau isomorphe à Kh où h désigne le nombre maximal de représentations irréductibles non isomorphes deux à deux. Cette anneau est composée de la somme directe des homothéties dans L(Si) si i varie de 1 à h.
![\mathbb K[G] \; \simeq \; \bigoplus_{i=1}^h \mathcal L_{\mathbb K}(S_i)\quad et \quad \mathbb D = \bigoplus_{i=1}^h \{f \in \mathcal L_{\mathbb K}(S_i) \; / \; \exists \lambda_i \in \mathbb K \quad f = \lambda_i.Id\}](https://static.techno-science.net/illustration/Definitions/autres/8/8a8d44267bdbf6eb80797e965866db06_b62cd0717495345925643cb7771cbba1.png)
Dans le cas d'une algèbre de groupe, il est possible de déterminer les éléments du centre par leur décomposition dans la base canonique (es) où s décrit G. On obtient la proposition suivante :
-
- Soit c une classe de conjugaison et dc la somme des éléments de la base canonique indexés par les éléments de c. Le centre de K[G] est l'espace vectoriel engendré par les éléments dc lorsque c parcourt l'ensemble des classes de conjugaison.
Le nombre h de représentations irréductibles différentes est donc égal au nombre de classes de conjugaison. Cette analyse fournit des résultats complémentaires de ceux obtenus par les caractères. Cette théorie indique que les caractères forment une base orthonormale de l'ensemble des fonctions centrales. La relation entre les deux est établie par la proposition suivante, si C désigne l'ensemble des classes de conjugaison :
-
- L'application φ défini ci-dessous, de l'espace des fonctions centrales KC dans le centre de K[G] est un isomorphisme d'algèbre sur K.
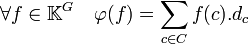
Pour cette raison, on identifie généralement le centre de l'algèbre et l'ensemble des fonctions centrales.
Le centre peut être vu de trois manières différentes, soit comme l'espace des fonctions centrales, soit comme une somme directe S d'algèbres d'endomorphismes d'espaces vectoriels LK(Si), soit comme un sous-espace vectoriel de K[G]. Si φ désigne l'isomorphisme de K[G] dans S, la relation entre les trois visions est la suivante, si χi est le caractère de Si et di la dimension de Si :
-
- Soit u un élément du centre de K[G] et us ses coordonnées dans la base canonique, l'image de u par φ est une somme directe d'homothéties sur Si de rapport λi avec :
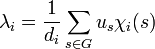
-
- Soit c une classe de conjugaison et dc la somme des éléments indéxés par c. Le centre de K[G] est l'espace vectoriel engendré par les éléments dc lorsque c parcourt l'ensemble des classes de conjugaison.
Montrons que dc est élément du centre :
Tout automorphisme intérieur restreint à c est une permutation et donc laisse dc invariant. En conséquence, si s est un élément de G, sdcs-1 = dc ou encore sdc = dcs, ce qui démontre que l'espace engendré par les dc est inclus dans le centre.
Réciproquement, montrons que le centre est combinaison linéaire des ec :
Il suffit de montrer que, si x est un élément du centre de K[G], son écriture comme combinaison linéaire des vecteurs de la base G possède des coefficients égaux pour deux éléments s et t conjugués. Soit Autu un automorphisme intérieur tel que son image de s soit égal à t. Soit p la projection sur l'espace vectoriel engendré par s et t parallèlement à l'espace vectoriel engendré par les autres éléments de G. Dire que x est un élément du centre revient à dire qu'il est stable par tous les automorphismes intérieurs, en particulier poAutu(x)=p(x). Soit λa le coefficient de x pour le vecteur a de la base G, alors p(x) est égal à λss + λtt, et il existe un élément v de G tel que poAutu(x) soit égal à λvs + λst. L'égalité poAutu(x)=p(x) montre que λss et λtt sont égaux, ce qui termine la démonstration.
-
- Soit u un élément du centre de K[G] et us ses coordonnées dans la base indicée par G, l'image de u par φ est une somme directe d'homothéties sur Si de rapport λi avec :
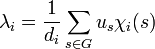
Si φi désigne la composante de φ dans LK(Si), par linéaité, φi(u) s'écrit de la manière suivante :
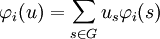
La trace de l'application est égale à di fois le rapport de l'homothétie, et donc, si Tr(φi(u)) désigne la trace de φi(u) alors elle est égale à di.λi et donc :
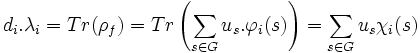
Orthogonalité
La complémentarité des deux approches, par les caractères et par l'algèbre du groupe s'applique aussi sur les propriétés d'orthogonalité. Soit (V1, ρ1) et (V2, ρ2) deux représentations de G :
-
- Si χ1 et χ2 désigne les caractères de ρ1 et ρ2 et si les représentations (V1, ρ1) et (V2, ρ2) sont considérées comme des G-module, alors l'égalité suivante est vérifiée :

En utilisant les notations précédentes, notons :
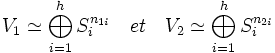
Le lemme de Schur démontre que dim HomKG (Si, Sj) = δij si i et j sont des entiers compris entre 1 et h et δij désigne le symbole de Kronecker. On en déduit :
![dim \; Hom_{\mathbb K}^G (V_1\, ,\, V_2)=dim \; Hom_{\mathbb K}^G \Big(\bigoplus_{i=1}^h S_i^{n_{1i}}\, ,\, \bigoplus_{j=1}^h S_j^{n_{2j}}\Big)=\sum_{ij \in [1,h]} n_{1i}.n_{2j}dim \; Hom_{\mathbb K}^G (S_i\, ,\, S_j)=\sum_{i=1}^h n_{1i}.n_{2i} \;](https://static.techno-science.net/illustration/Definitions/autres/a/aa0017f2bc89202b461e061492cda573_c1248178beaebc730beeaa95e5263fb3.png)
La propriété d'orthonormalité des caractères irréductibles permet de conclure.

















































