Algèbre d'un groupe fini - Définition
La liste des auteurs de cet article est disponible ici.
Définitions
Algèbre d'un groupe
Les notations suivantes sont utilisées dans tout l'article. G désigne un groupe fini noté multiplicativement, son élément neutre est noté 1 et son ordre g. K est un corps commutatif de caractéristique soit nulle soit première avec g.
-
- La K-algèbre du groupe G, noté K[G] est l'espace vectoriel des combinaisons linéaires formelles des éléments de G, il est muni de la multiplication suivante :
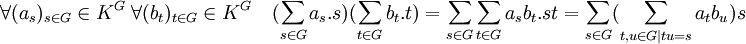
La construction rigoureuse d'une telle algèbre est présentée dans l'article polynôme en plusieurs indéterminées, dans le paragraphe sur l'algèbre d'un monoïde. Une telle structure bénéficie de la propriété suivante :
-
- La structure K[G] est celle d'une algèbre associative sur un corps.
Quelques définitions sont nécessaires, elle concerne les algèbres en général :
-
- Une algèbre est dite simple si les seuls idéaux bilatères sont {0} et l'algèbre elle-même.
- Un idéal est dit facteur direct si et seulement s'il existe un idéal bilatère sous-espace supplémentaire.
- Une algèbre est dite semi-simple si et seulement si toute sous-algèbre simple est facteur direct.
Une algèbre de groupe possède la propriété suivante appelée théorème de Maschke :
-
- Si l'ordre du groupe n'est pas un multiple de la caractéristique du corps K, alors l'algèbre du groupe est semi-simple.
G-module
-
- Un module sur l'anneau de l'algèbre du groupe K[G] est appelé un G-module.
Le théorème de Maschke démontre qu'un G module est semi-simple. En conséquence il bénéficie de la propriété suivante :
-
- En dimension finie, un module est semi-simple si et seulement si elle est somme directe de sous-module simples.
La démonstration est donnée dans l'article associé. Cette propriété se transpose immédiatement à l'algèbre de groupe.
La structure multiplicative de l'anneau restreint à GxV si V désigne le G module définit une représentation. Réciproquement tout morphisme d'une représentation se prolonge par linéarité sur K[G]. En conséquence, il existe donc une équivalence stricte entre la notion de G-module et celle de représentation.
-
- Soit V1 et V2 deux G-modules, la notation homKG(V1, V2) désigne la K-algèbre des morphismes de G-module de V1 dans V2.
Un tel morphisme φ vérifie les propriétés suivantes:
![\forall \alpha ,\beta \in \mathbb K \quad \forall a,b \in V_1 \quad \forall k \in \mathbb K[G]\quad \varphi (\alpha a + \beta b) = \alpha \varphi (a) + \beta \varphi (b) \quad et \quad \varphi (k.a) = k. \varphi (a) \quad](https://static.techno-science.net/illustration/Definitions/autres/e/ec80da5c572cf5d566b12e5b1150e965_b4c91151bbcd1cd8c44cbba46a7ba4bb.png)
Applications
Réciprocité de Frobenius
Un bon exemple d'utilisation de la structure d'algèbre de groupe est donné par le critère de réciprocité de Frobenius. Il concerne un mode de construction de G-module appelé représentation induite. Soit H un sous-groupe de G et W un K[H]-module. Alors la structure suivante est le G-module induit par W :
![V\simeq K[G]\otimes_{K[H]}W \;](https://static.techno-science.net/illustration/Definitions/autres/3/3ff6501e2ed1de5bfe91ffa7fbef9046_0b172953c4c8c2ebd51ae20fd5807dd4.png)
La représentation induite correspond, à une extension des scalaires K[H] à l'anneau K[G] sur le H-module W. Dans le cas où H est un sous-groupe normal de G, le G-module induit est l'équivalent d'un produit semi-direct.
Le critère de réciprocité de Frobenius est une méthode simple pour calculer le produit hermitien du caractère d'un module induit. Si ψ désigne le caractère de la représentation θ issus du H-module W et χ celui d'une représentation ρ de G, si Ind ψ désigne le caractère d'une représentation induite, c’est-à-dire la représentation associée au module induit et Res χ le caractère de la restriction de ρ à H, alors :

Elle se démontre en établissant un isomorphisme entre les deux structures de morphismes de K-algèbre associée, l'égalité des dimensions permet de conclure.
Entier algébrique
Le centre de K[G] est un anneau commutatif sur le corps K, une extension des rationnels. En conséquence, il est possible de parler d' entier algébrique sur cet ensemble. Cet approche est largement utilisée pour l'analyse de l'algèbre d'un groupe fini, ce paragraphe est un exemple. Notons c les classes de conjugaisons et dc la somme des éléments de c.
-
- Soit u un élément du centre de K[G] tel que toutes ses coordonnées dans la base (dc) soit entières (au sens algébrique) sur K, alors u est un entier algébrique.
Comme u est combinaison linéaire à coefficients dans les entiers algébriques des valeurs dc, il suffit de montrer que ces valeurs sont des entiers algébriques. Soit a et b deux classes de conjugaisons, dadb est combinaison linéaire à coefficients entiers des dc, en conclusion le Z-module est de type fini, ce qui montre que la famille des dc est composée d'entiers algébriques. Or, u est combinaison linéaire à coefficients entiers algébriques d'entiers algébriques, ce qui démontre le résultat.
Avec les notations du paragraphe précédent, on dispose de la propriété :
-
- Soit u un élément du centre de K[G] tel que toutes ses coordonnées soit entières (au sens algébrique) sur K, alors le nombre suivant est un entier algébrique.
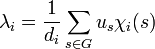
Considérons l'image de u par φi, φi(u) est un élément du centre de L(Si), et φi est un morphisme d'algèbre. En conséquence φi(u) est un entier algébrique du centre de L(Si), c’est-à-dire de l'espace des homothéties de Si, isomorphe au corps K. Le rapport de l'homothétie est donc un entier algébrique de K.
On en déduit la propriété suivante :
-
- Le degré di d'une représentation irréductible divise l'ordre g du groupe.
Considérons l'élément u égal à la somme si s décrit G des éléments χi(s-1).s, le caractère d'un élément de s est la trace d'un endomorphisme admettant Xg - 1 comme polynôme annulateur. La trace est donc somme de racines g-ième de l'unité est donc à valeur dans les entiers algébriques. La fonction χi est un caractère donc une fonction centrale de G, ceci démontre que u est bien un élément du centre de G à coefficients dans la base G donc entiers algébriques. La proposition précédente s'applique et la valeur g/di est celle d'un entier algébrique, c'est aussi un nombre rationnel et donc un élément de Z. Ce qui démontre que di divise l'ordre du groupe.
Groupe abélien
Si le groupe est abélien, il est aisé d'établir le groupe dual de G. Il est fini et isomorphe à G. L'algèbre du groupe complexe possède alors tous les outils de l'analyse harmonique. On définit une transformée de Fourier et un produit de convolution, et les théorèmes comme l'égalité de Parseval, le théorème de Plancherel ou la dualité de Pontryagin s'appliquent.
Il existe de nombreuses application à l'analyse harmonique sur un groupe abélien fini, on peut citer en arithmétique la constitution d'outils comme le symbole de Legendre, les sommes de Gauss utilisées pour la démonstration de la loi de réciprocité quadratique ou pour le calcul des périodes de Gauss et la recherche des racines du polynôme cyclotomique.

















































