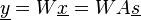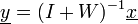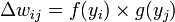Analyse en composantes indépendantes - Définition

Séparation de source (problème de la soirée cocktail)

L'illustration classique de la séparation de sources est le problème de la soirée cocktail (cocktail party problem). Lors d'une telle soirée, on dispose P microphones dans une salle dense, où N personnes discutent par groupes de tailles diverses. Chaque microphone enregistre la superposition des discours des personnes à ses alentours et le problème consiste à retrouver la voix de chaque personne (« débarrassée » des autres voix considérées comme parasites).

Lors d'une soirée cocktail, bien que les discussions soient multiples et mêlées, un humain est capable de séparer le flux sonore qui l'intéresse (la voix de son interlocuteur) et d'ignorer les autres.

L'ACI permet de résoudre ce problème en considérant simplement que les personnes qui parlent à un instant donné ont des discours « indépendants ». Il ne s'agit pas de prendre en compte la sémantique de ces discours (on peut en effet espérer que certaines voix soient concordantes à ce niveau!) ni même l'acoustique (ce qui serait faux, ne serait-ce que lorsque les interlocuteurs ont des langues identiques...), mais de les considérer comme des signaux aléatoires statistiquement indépendants. Au contraire d'une chorale, les gens qui parlent en même temps à un instant donné émettent des sons indépendants.

La théorie assurant ce résultat pose néanmoins quelques hypothèses, en particulier que « le nombre de micros est supérieur ou égal au nombre de personnes ». Symétriquement, il reste aussi des indéterminations sur le résultat (les voix séparées). Celles-ci peuvent être interprétées de la façon suivante:

• on ne peut pas attribuer les voix aux personnes avec la seule connaissance des signaux retrouvés (mais un auditeur humain le pourrait). Autrement dit, on ne connaît pas l'ordre des signaux retrouvés.
• on ne connaît pas l'intensité de la voix des locuteurs. Celle-ci sera attribuée arbitrairement et un auditeur humain ne pourrait se fier qu'au ton de la voix et à la connaissance de la personne pour le déterminer.

Pour des raisons historiques et pédagogiques, l'ACI est souvent introduite comme permettant de résoudre le problème de séparation de sources. Néanmoins, il existe d'autres méthodes pour résoudre ce problème, ne faisant pas appel strictement à l'hypothèse d'indépendance statistique entre sources (la parcimonie par exemple).

Principaux algorithmes

Le but de cette section est de donner les principales idées des algorithmes les plus connus permettant de résoudre le problème d'ACI. Ces algorithmes ont été choisis de manière à présenter un panel varié d'approches. On trouvera de nombreuses autres méthodes dans la littérature scientifique.

Nous considérons ici le modèle linéaire instantané non bruité et cherchons une estimation y_i des sources indépendantes s_i ainsi qu'une matrice de séparation W vérifiant:

Algorithme HJ

Architecture de l'algorithme HJ.

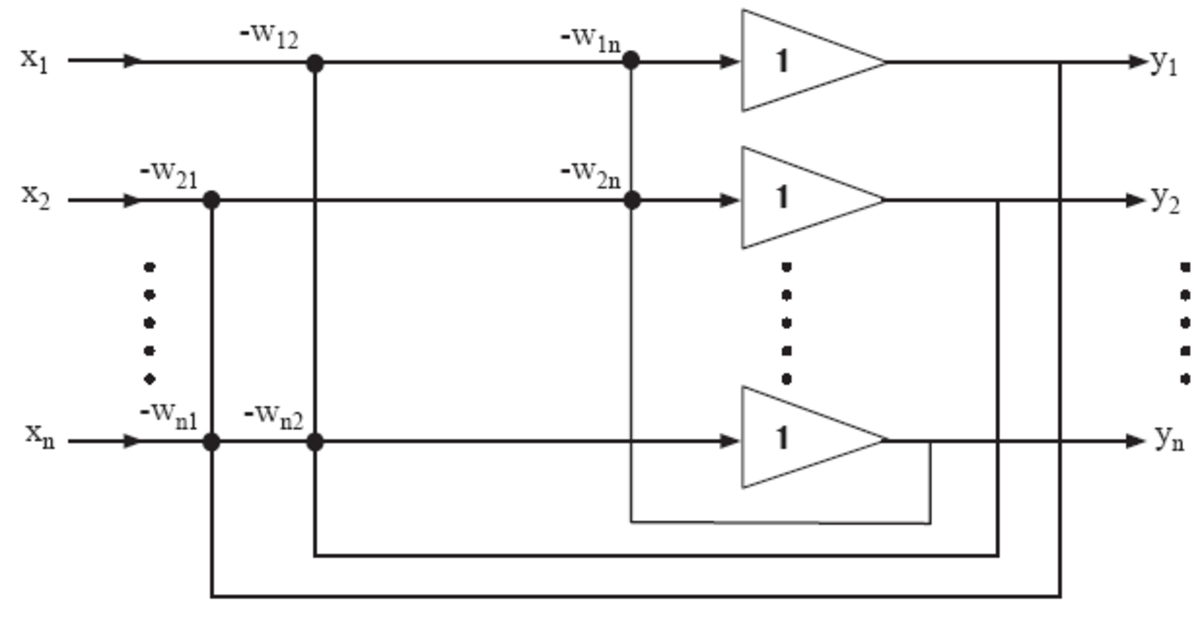
Le premier algorithme d'ACI (du nom de ses auteurs) procède d'une approche neuromimétique: il s'agit d'une utilisation des outils du traitement du signal pour modéliser un phénomène inspiré du fonctionnement neuronal. Cet algorithme était de type Robins-Monro, et recherchait itérativement des zéros communs de deux fonctions. Il est basé sur un réseau de neurones récursif dont les poids sont les termes non diagonaux de la matrice de séparation W, les termes diagonaux étant contraints à la nullité. L'estimation des sources est ainsi donnée par:

Avec la règle d'adaptation suivante pour les termes non diagonaux:

f(.) et g(.) étant des fonctions non linéaires impaires différentes à choisir en fonction des densités de probabilité des sources à estimer. Des travaux ultérieurs ont justifié la forme de cette règle d'apprentissage et ont montré que la fonction non linéaire devait être choisie au sens du maximum de vraisemblance. La mesure d'indépendance sous-jacente à cet algorithme est l'annulation des cumulants d'ordre supérieur.

Maximisation de Contraste (CoM)

Cette famille d'algorithmes a été proposée par Comon en 1991. Ces algorithmes procèdent en balayant toutes les paires de sorties à tour de rôle. L'algorithme CoM peut calculer soit tous les cumulants des observations (comme JADE), soit à la demande, à chaque fois qu'une rotation optimale est calculée. Le choix peut être fait de manière a minimiser la complexité numérique.

Plusieurs versions ont été proposées, suivant le contraste utilisé. En 1991, il s'agissait par exemple de la somme des modules carrés des cumulants marginaux des sorties: ce contraste est maintenant appelé CoM2. Plus tard, un autre contraste, CoM1, a été proposé par Moreau: la somme des modules des cumulants marginaux des sorties. Lorsque les sources ont des cumulants marginaux toutes de même signe, il a été montré que la valeur absolue peut être retirée. Cette simplification a donné lieu à une autre solution algébrique compacte, développée par Comon.

D'autres formes plus générales de contraste basés sur les cumulants ont été ensuite proposées dans la littérature.

JADE

(Joint Approximate Diagonalization of Eigenmatrices)

Un tenseur de cumulants (à l'ordre quatre) est une matrice à quatre dimension contenant tous les cumulants croisés d'ordre quatre. C'est aussi une application linéaire d'un espace de matrice de taille NxN dans un autre espace de matrice de même taille. La diagonalisation de cette application linéaire permet d'effectuer la séparation voulue sous certaines conditions. En effet, l'indépendance statistique est vue ici comme la recherche à tendre vers la nullité de tous les moments et cumulants (à tous les ordres), ce qui revient à annuler tous les éléments non diagonaux de la matrice associée à l'application linéaire sus-citée. Cardoso et Souloumiac ont proposé une méthode de diagonalisation jointe permettant de mettre en pratique ce principe. Cela revient à minimiser la somme du carrés de tous les cumulants (à l'ordre quatre) « hors diagonale » (cumulant entre deux signaux différents). En pratique, JADE nécessite le calcul de tous les cumulants d'ordre quatre et a donc une complexité en O(n⁴).

Fast-ICA

Hyvarinen et Oja proposent d'estimer les composantes indépendantes au moyen d'une mesure de « non gaussianité ». En effet, le théorème central limite stipule que la somme de variables indépendantes tend asymptotiquement vers une distribution normale. Dans le cas considéré, les estimations sont une telle somme de variables indépendantes ( ) et tendent donc vers une distribution gaussienne. En cherchant à maximiser la non gaussianité de , chacune de ses composantes tendra vers une estimation des sources indépendantes (aux deux indéterminations près). Plusieurs mesures de « non gaussianité » ont été proposées, la plus usitée étant la néguentropie qui est la différence entre l'entropie d'une variable gaussienne et l'entropie du vecteur mesuré. Hyvarinen a proposé différentes approximations de cette mesure permettant une mise en œuvre algorithmique du principe exposé.

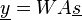
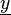
Pour éviter que toutes les estimations convergent vers la même source, il est nécessaire d'imposer l'orthogonalité des y_i (sous contrainte de blanchiment, cela revient à décorreler les données, au moyen d'une analyse en composantes principales par exemple). Deux méthodes existent pour imposer cette orthogonalité. La version dite « par déflation » estime itérativement les sources et orthogonalise chaque estimation au moyen d'un procédé de Gram-Schmidt. La version « symétrique » orthogonalise simultanément toutes les estimations.

« Fast-ICA » met ainsi en évidence de forts liens entre l'analyse en composantes indépendantes et la poursuite de projection.

Infomax

Formulé par Linsker, ce principe stipule que l'implémentation d'un modèle des capacités cognitives des mammifères au moyen d'un réseaux de neurones artificiel doit être telle que le taux d'information transmis d'une couche de neurones à la suivante soit maximal. Ce taux d'information peut notamment être mesuré par l'entropie lorsque l'on se place dans le formalisme de Shannon.

Nadal et Parga ont montré que sous certaines conditions, ce principe était équivalent au principe de réduction de redondance qui énonce que le but des systèmes sensoriels des mammifères est de coder efficacement les stimuli (visuels, sonores...). En se plaçant à nouveau dans le formalisme de Shannon, cela revient à minimiser la redondance d'information de leur environnement et obtenir un codage factoriel (i.e un codage qui minimise les dépendances statistiques entre dimensions, aussi appelé codage à entropie minimale).

Bell et Sejnowsky ont exploité cette équivalence en l'écrivant:

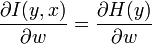
où est l'information mutuelle entre les sorties et les entrées d'un réseau de neurones, les paramètres de ce réseau et l'entropie des sorties. Le relation ci-dessus exprime exactement que rendre maximale l'information mutuelle des sorties des réseaux (i.e obtenir un code factoriel le plus efficace possible) est identique à rendre maximale l'information qui « passe » à travers le réseau.

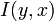
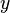
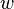
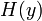
Ils en déduisirent une règle d'apprentissage des paramètres du réseau qui, après quelques simplifications et l'exploitation d'une règle du type « gradient relatif », revient à:

ΔW = [I − Ktanh(y)y^T − yy^T]W

K étant une matrice diagonale dont les éléments valent 1 pour les sources sur-gaussiennes et -1 pour les sources sous-gaussiennes.

Il a été montré une équivalence de cette approche et de l'approche par maximum de vraisemblance.