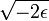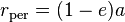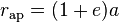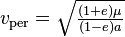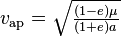Apsides - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Terminologie - Formules détaillées - Positions relatives des apsides des planètes du système solaire

Introduction

Diagramme de Kepler des éléments orbitaux. F périapse, H apoapse, la ligne rouge entre eux est la ligne des apsides.

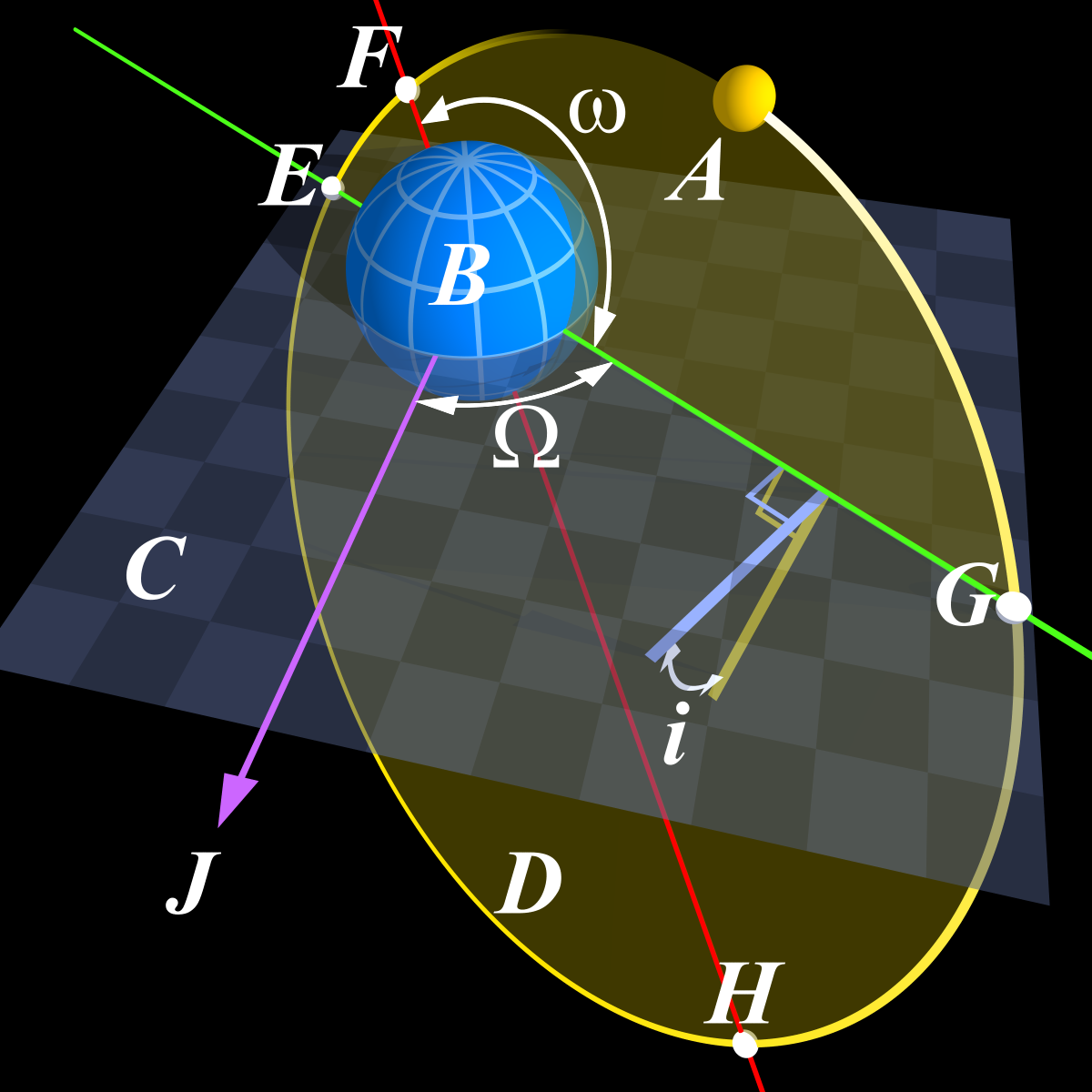
Apsides, en astronomie, désigne les deux points extrêmes de l'orbite d'un objet céleste pour lesquels la distance est minimale (apside inférieure, ou périapside ou périapse) ou maximale (apside supérieure, ou apoapside, ou apoapse) par rapport au foyer de cette orbite.

Le mot s'emploie plus rarement au singulier pour désigner l'un ou l'autre des deux points.

La ligne qui relie le périapside et apoapside d'une orbite donnée est appelée ligne des apsides. C'est l'axe principal de l'ellipse, la ligne la plus longue qui joigne les 2 points les plus éloignés.

Terminologie

Dans le cas d'une étoile et des principaux objets du système solaire, un terme spécialisé apparenté peut être employé comme indiqué dans le tableau ci-dessous. Le nom de ces points de plus petit et plus grand éloignement dépendent du corps central ; ils sont formés en prenant la racine grecque du nom de ce corps, qui est en général le nom d'un dieu.

Toutefois, seuls les couples périhélie et aphélie, périgée et apogée, périastre et apoastre sont couramment utilisés.

corps central	racine grecque	périapside	apoapside
Galaxie	galaxias (gala=lait ; voie lactée)	Périgalacticon	Apogalacticon
Trou noir	mélos (noir)	Périmélasme	Apomélasme
Étoile	asteros	Périastre	Apoastre
Soleil	Hélios (personnifie le Soleil)	Périhélie	Aphélie'
Mercure	Hermès (dieu du commerce)	Périherme	Apherme
Vénus	Cythère	Péricythère	Apocythère
Terre	Gaïa (déesse de la terre mère)	Périgée	Apogée
Lune	Séléné (déesse de la pleine lune)	Périsélène	Aposélène
Mars	Arès (dieu de la fureur guerrière)	Périarée	Apoarée
Jupiter	Zeus (roi des dieux)	Périzène	Apozène
Saturne	Cronos (roi des Titans)	Périkrone	Apokrone
Uranus	Ouranos (personnifie le ciel)	Périourane	Apourane
Neptune	Poséidon (dieu de la mer)	Périposéide	Apoposéide
Pluton	Hadès (maitre des Enfers)	Périhade	Aphade

Les termes périlune ou apolune (pour le satellite naturel d'une lune), périjove ou apojove (pour un satellite de Jupiter) sont à éviter.

On voit parfois aussi les termes péricynthe ou apocynthe dans le cas d'un satellite artificiel de la Lune.

Formules détaillées

Les formules suivantes permettent de calculer la distance de chacun des apsides au centre de masse, et la vitesse en ces points :

	périapside	apoapside
distance	$r_\mathrm{per}=(1-e)a\!\,$	$r_\mathrm{ap}=(1+e)a\!\,$
vitesse	$v_\mathrm{per} = \sqrt{ \tfrac{(1+e)\mu}{(1-e)a} } \,$	$v_\mathrm{ap} = \sqrt{ \tfrac{(1-e)\mu}{(1+e)a} } \,$

Selon les lois de Képler sur le mouvement des planètres (conservation du moment angulaire) et les principes de la conservation de l'énergie, les quantités suivantes sont constantes pour une orbite donnée :

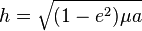
moment angulaire relatif spécifique : $h = \sqrt{(1-e^2)\mu a}$
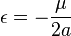
énergie orbitale spécifique : $\epsilon=-\frac{\mu}{2a}$

avec :

$a\!\,$ est la longueur du demi grand axe
$\mu\!\,$ est le paramètre gravitationnel standard (produit de la constante de gravitation "grand G" par la masse "M" du corps central).
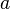
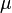
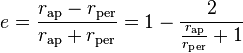
$e\!\,$ est l'excentricité orbitale définie par $e=\frac{r_\mathrm{ap}-r_\mathrm{per}}{r_\mathrm{ap}+r_\mathrm{per}}=1-\frac{2}{\frac{r_\mathrm{ap}}{r_\mathrm{per}}+1}$

Attention : Pour convertir la distance mesurée depuis les surfaces des objets en distance mesurée depuis les centres de gravité, il faut ajouter le rayon des objets en orbite ; et réciproquement.

La moyenne arithmétique des deux distances extrêmes est la longueur du demi grand axe $a\!\,$ de l'ellipse orbitale. La moyenne géométrique de ces deux mêmes distances est la longuer du demi petit axe $b\!\,$ de l'ellipse orbitale.

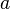
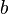
La moyenne géométrique des deux vitesses limites $\sqrt{-2\epsilon}$ , est la vitesse correspondant à une énergie cinétique qui, à n'importe quelle position sur l'orbite, ajoutée à l'énergie cinétique courante, permettrait à l'objet en orbite de s'échapper de l'attraction. La racine carrée du produit des deux vitesses est donc la valeur locale de la vitesse de libération.