Construction du nombre chez l'enfant - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La construction du nombre chez l'enfant est une voie de recherche de la psychologie du développement. Les premières recherches scientifiques à ce sujet, ont été réalisées par Jean Piaget.
Historique
Pythagore puis, plus tard, Descartes, placent l'origine de l’intelligence dans le don de Dieu : « c'est de ce doute universel que, comme d'un point fixe et immuable, j'ai résolu de dériver la connaissance de Dieu, de vous-même, et de tout ce que renferme le monde. » (Descartes, Recherche de la vérité par les lumières naturelles). Darwin, dans sa théorie de l’évolution parle de l'« évolution naturelle de l’intelligence », et exclut ainsi Dieu de son analyse.
Jean Piaget et Jean-Pierre Changeux vont reprendre cette idée avec le « darwinisme neuronal mental ». Dès lors, ce thème de la construction du nombre est resté au premier plan de la psychologie développementale, et a connu une émergence de nombreuses recherches, qui ont débouché sur de nombreuses découvertes. Du point de vue pratique, on peut penser que ces dernières pourront être exploitées dans le cadre de l’amélioration de l’apprentissage de l’arithmétique pour l’enfant.
La théorie de Piaget
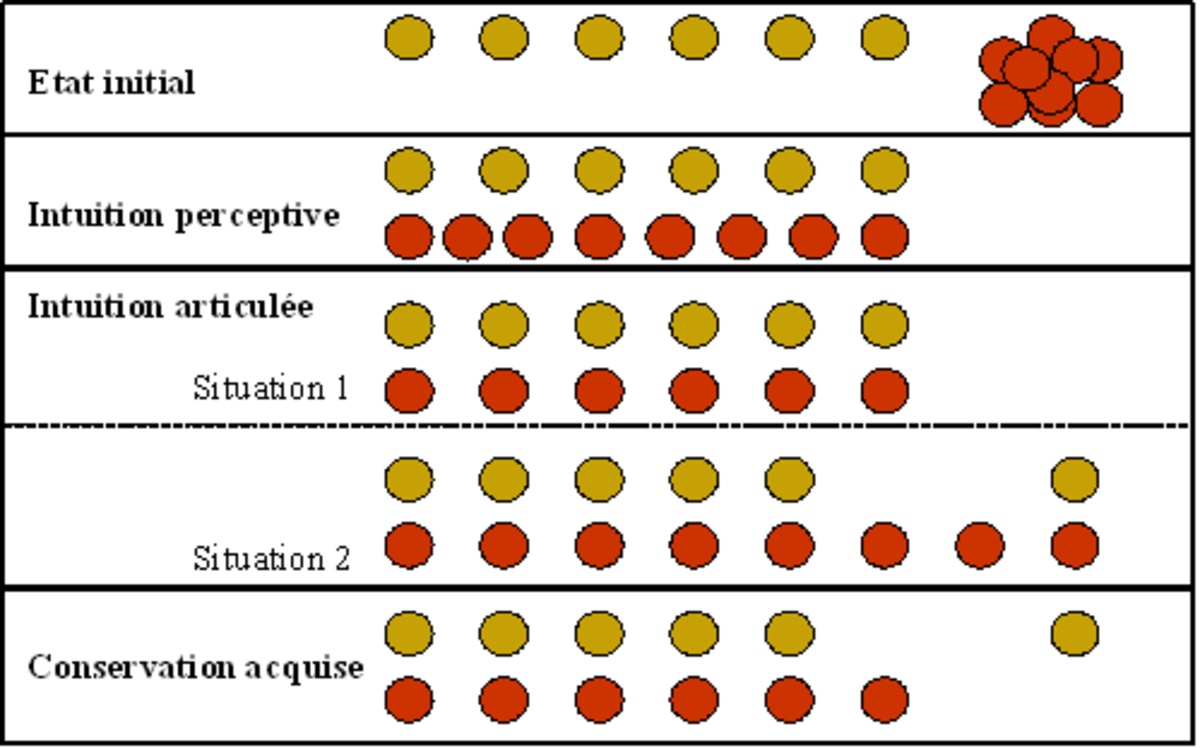
Pour Piaget et Szeminska (1941 ; 1967), le concept de nombre chez l’enfant, ne prend naissance qu’au moment du stade des opérations concrètes, s’appuyant et dépassant des niveaux d’acquisitions antérieurs. L’épreuve clé de ce stade Piagétien est celle de la conservation du nombre (opération logico-mathématique), qui est réussie par l’enfant autour de sept ou huit ans.
Ce n’est donc que vers cet âge que l’enfant atteint le niveau de « conservation acquise », où il aligne le même nombre de jetons que l’expérimentateur, en dépassant la simple perception qui l’induisait en erreur auparavant. L'enfant donne alors des réponses caractéristiques de l’acquisition de la conservation selon Piaget. Pour Piaget, le nombre se construit par une synthèse logico-mathématique entre les opérations de classification et de sériation.
Cette vision va donc dans le sens d’une performance du nombre acquise par le déploiement de capacités successives indispensables, pour finir par atteindre un niveau optimal, qui correspond à la période où l’enfant devient « conservant ». « Ainsi, Piaget concevait la genèse de la notion de nombre comme un processus essentiellement endogène de coordination d’actions devenant progressivement réversibles ».
Mais cette conception a été fortement bousculée ces dernières années, avec l’aide de l’évolution des possibilités techniques offertes aux chercheurs contemporains, qui peuvent aujourd’hui étudier plus précisément les capacités des enfants d’âge préverbal. Ces recherches ont pu montrer une certaine capacité numérique précoce.
Le calcul chez le jeune enfant
En 1992, une chercheuse publie un article sur la capacité de calcul chez le bébé humain, qui va déclencher de nombreuses réactions.
Réaction aux événements impossibles
Wynn, en 1992, a établi une procédure expérimentale, afin d’étudier chez des bébés de quatre et cinq mois leur capacité à faire des calculs simples tels que l’addition et la soustraction.
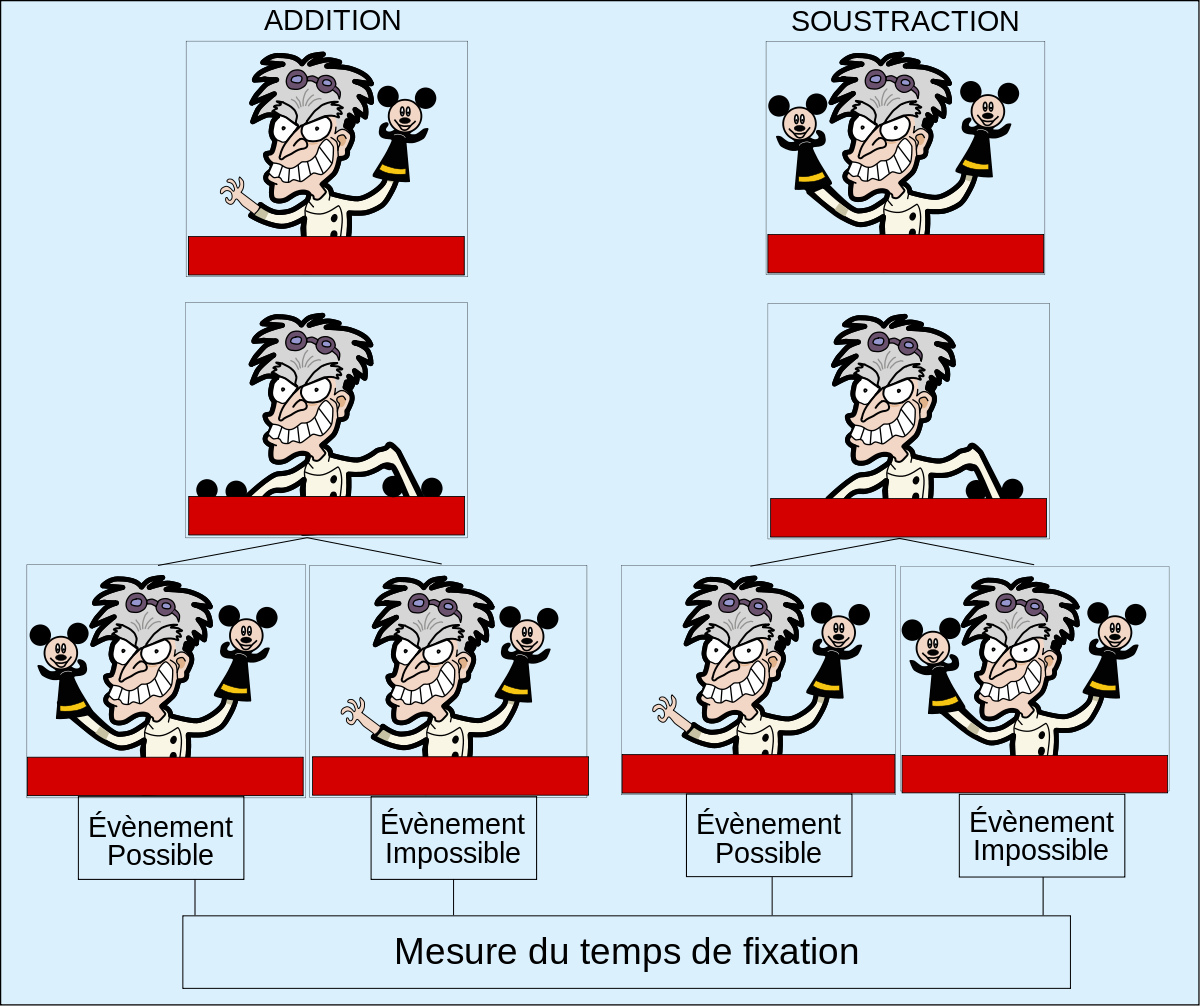
Ainsi elle utilise un petit théâtre de marionnettes, avec des personnages attirants l’attention des enfants (Mickey Mouse), et elle introduit des événements impossibles afin de mesurer le temps de fixation de l’enfant. Ce temps devra déterminer si l’enfant « estime » l’événement possible, ou transgressant une loi physique.
Dans la situation d’addition, les enfants réagissent à l’événement impossible (1+1=1), en fixant la scène plus longtemps. Dans la situation de soustraction, l’auteur constate qu’il en est de même pour l’évènement (2 -1=2).
Ainsi Wynn en conclut que les enfants de quatre et cinq mois ont des capacités précises du nombre, et pas seulement une dichotomie entre unique et plusieurs. De plus, on peut noter que pour réussir l’épreuve, les bébés devaient avoir acquis la permanence de l'objet.
Critiques faites à Wynn et leur réponse par Wynn et Houdé
Dans la lettre du LPEQ, on peut lire un résumé d’une conférence de Jacqueline Bideaud, qui dit que « les résultats de Wynn seraient davantage liés à la permanence de l'objet et à la capacité de l’enfant de se représenter deux objets discrets (sur la base d’informations spatio-temporelles en particulier) qu’à des compétences arithmétiques précises préalables. Cette construction du discret serait la racine du comptage exact ».
Il est vrai que la question que l’on peut se poser à la suite de l’expérience de Wynn, c’est est-ce que l’on peut être sur que l’enfant a bien traité numériquement les objets, et pas de façon globale, c'est-à-dire en se « disant » qu’un mickey plus un mickey allait faire plus que un. Cela viendrait donc d’un traitement physique et non mathématique.
Wynn a donc, en réponse, refait son expérience, mais en intégrant l’événement impossible 1+1=3. Ainsi, si le bébé réagit à cet événement, on devra exclure le fait que l’enfant raisonne en termes de « plus que un ». Vérification faite, l’expérience a confirmé la précédente.
Si l’on souhaitait comparer les résultats de Piaget à ces derniers, il fallait mettre en place une expérience avec des grands nombres, et non plus qu’avec des petits nombres, et il fallait tester l’enfant au niveau langagier. Ainsi, Olivier Houdé, réalise une expérience basée également sur les réactions aux événements impossibles, mais chez des enfants de deux et trois ans (âge du langage articulé). La question que s’est posé l’auteur a été «est-ce que le jeune enfant va être l’héritier cognitif, intellectuel du bébé compétent qu’il était, […] est-ce que l’on va retrouver ce synchronisme des réactions aux événements impossibles, 1+1=1 et 1+1=3, qui était le critère d’un calcul précis? »
Dès lors, il va utiliser le même nombre de même objet (des Babars), pour tester la capacité numérique des enfants, dans la situation de Wynn et de Piaget.
Chez l’enfant d’école maternelle, il y a un décalage entre la première et la seconde expérience. En effet, dans la procédure de Piaget, on ne constate pas d’utilisation du nombre, alors que dans la situation de Wynn, on le remarque. De plus, les enfants de deux ans réagissent bien face à 1+1=1, mais ils ne réagissent plus à l’événement 1+1=3. Ainsi, on ne retrouve pas ce « synchronisme des réactions aux événements impossibles » chez l’enfant de deux ans, ce qui montre qu’il est moins capable que l’enfant de quatre ou cinq mois.
En revanche, à trois ans, les enfants réussissent à nouveau la constatation que 1+1=3 est impossible, mais échouent toujours dans la situation de Piaget. Dès lors, on peut se demander qu’elle en est la raison.
Houdé explique la non réussite des enfants de deux ans, par le fait que le langage pourrait interférer sur le nombre. En effet, c’est la période où l’enfant apprend, entre autres, la différence entre singulier et pluriel, ce qui peut le perturber. Ce serait la stratégie utilisée pour l’expérience de Piaget par l’enfant de trois ans (stratégie longueur égale nombre), qui poserait problème, et qui expliquerait que l’enfant échoue à l’expérience Piagétienne, et pas à celle de Wynn. En effet, cette stratégie est très souvent utilisée par tous, et elle est souvent efficace. Cependant, dans ce cas précis, elle échoue.
Houdé émet l’hypothèse que la différence entre les enfants de trois ans et ceux de sept ans, est la capacité d’inhiber cette stratégie courante, afin d’utiliser la stratégie numérique qui est plus adéquate. L’enfant de cet âge serait donc en mesure de manipuler le nombre, mais uniquement sous certaines conditions.
Afin de vérifier cette hypothèse, Houdé et Guichart ont mis en place une expérience se basant sur une version informatisée de l’épreuve de Piaget. Ainsi les auteurs peuvent utiliser la chronométrie mentale afin de vérifier s’il y a bien inhibition de stratégie pour la réussir.
Donc les chercheurs installent des enfants de huit ans devant un écran d’ordinateur où on trouve deux lignes de « jetons numérisés ». Les sujets doivent dire s’il y a le même nombre de jetons sur la ligne du bas, que sur celle du haut, et leur réponse doit être donnée le plus rapidement possible. Cependant, deux types de situations sont présentés. Parfois la stratégie «longueur égale nombre» est efficace, alors que d’autres fois elle ne l’est pas. L’écran qui suivra l’un ou l’autre sera un écran où la stratégie « longueur égale nombre » est efficace.
Si le premier écran (amorce) est celui où l’enfant doit inhiber la stratégie « longueur égale nombre », alors il met plus de temps à répondre au second écran (cible). En revanche, si l’amorce coïncide avec la stratégie « longueur égale nombre », alors l’enfant répond plus rapidement.
Lors de la présentation du premier écran (première situation), l’enfant inhibe la stratégie « longueur égale nombre » pour réussir, et donc met plus de temps pour réussir le second écran, car un temps est nécessaire pour permettre la levée de l’inhibition. Cela révèle une compétition entre deux stratégies.
Calculs avec de grandes numérosités
McCrink et Wynn ont réalisé en 2003 une expérience, pour répondre à la critique de son étude précédente, qui dit que l’enfant en bas âge n’aurait pas de réelle capacité numérique, mais s’appuierait sur des « processus de cheminement spécialisés qui s'appliquent seulement sur des petits nombres » .
Ainsi, vingt six enfants âgés de six mois ont participé à l’étude et ont été divisés en deux groupes (additions Vs soustractions). Chaque groupe a eu des nombres approximativement égaux de garçons et de filles. Les sujets sont placés devant un écran d’ordinateur, et sont exposés soit à la procédure d’addition, soit à celle de soustraction.
Lors de la première, cinq objets descendent vers le bas de l'écran, et sont cachés peu après par un cache oculaire qui les recouvre entièrement. C’est alors que cinq objets additionnels émergent et disparaissent à leur tour derrière le cache oculaire.
Lors de la seconde procédure (soustraction), ce n’est plus cinq, mais dix objets qui sont dissimulés derrière le cache oculaire. Peu après cinq objets se déplacent en dehors du cache et sortent de l’écran. Dans les deux cas, le cache se laisse tomber, pour laisser apparaître, soit cinq, soit dix objets, et ainsi l’enfant découvre, soit un événement impossible, soit un événement possible.
Ainsi, les enfants en bas âge qui ont vu une opération d'addition ont regardé plus longtemps lorsque cinq objets apparaissaient (10,28 s) que lorsqu’il y en avait dix (7,35 s). Tandis que les enfants en bas âge qui ont vu une opération de soustraction ont regardé plus longtemps les écrans finaux avec dix objets (9.13 s) que ceux avec cinq (8.00 s).