Forme sesquilinéaire - Définition

Introduction

En algèbre, une forme sesquilinéaire sur un espace vectoriel complexe E est une application de E × E dans , linéaire selon l'une des variables et semi-linéaire par rapport à l'autre variable. Elle possède donc une propriété de « un-et-demi » linéarité (cf. sesqui). C'est l'équivalent complexe aux formes bilinéaires réelles.

Les formes sesquilinéaires les plus étudiées sont les formes hermitiennes. Parmi celle-ci, les formes hermitiennes définies positives permettent de munir E d'un produit scalaire et ouvrent à l'étude des espaces hermitiens, des espaces préhilbertiens complexes et des espaces de Hilbert.

Définitions et conventions

Forme semi-linéaire : Soit E un -espace vectoriel, une application φ de E dans est semi-linéaire (ou antilinéaire) si :

Elle respecte l'addition et presque la multiplication scalaire : pour tous x, y de E, pour tout λ de  : où est le conjugué de λ

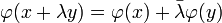
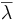
Une application semi-linéaire vérifie : f(ix) = − if(x), ce qui justifie l'autre terme utilisé : application anti-linéaire.

Les conventions qui suivent imposent un choix de l'argument qui est linéaire. Le choix ci-dessous (forme sesquilinéaire à gauche : première variable semi-linéaire, deuxième variable linéaire) est utilisé par tous les physiciens, ceci étant dû à l'origine à l'utilisation de la notation bra-ket (peut-être pas universel), mais le choix opposé est courant en mathématiques depuis les années 1950.

Forme sesquilinéaire (à gauche) : Une application f de E × F → est une forme sesquilinéaire (à gauche) si :

a) Elle est linéaire à droite : pour tout x de E, y, y' de F, pour tout λ de  :

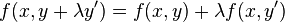
b) Elle est semi-linéaire à gauche, ce qui signifie que pour tout x, x' de E et y de F, pour tout λ de  : .

Les formes sesquilinéaires (à gauche) constituent un sous-espace vectoriel complexe de l'espace des applications de E x F dans C.

Exemples

• En dimension finie, on prouve que les seules formes sesquilinéaires à gauche sont les applications définies dans une base par :

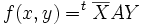
où X et Y sont les vecteurs colonnes, coordonnées de x et y dans la base (e₁,...,e_n), et où A est la matrice définie par .

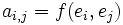
L'espace vectoriel complexe des formes sesquilinéaires (à gauche) sur un espace vectoriel de dimension n est donc isomorphe à l'espace vectoriel des matrices carrées . Les formes sesquilinéaires hermitiennes correspondent aux matrices telles que .

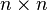
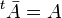
• Soit B un ensemble non vide et le -espace vectoriel des applications de B dans , et soient a et b deux éléments de B. La forme f_a,b définie par est une forme sesquilinéaire (à gauche) à symétrie hermitienne.

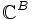
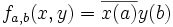
Formes hermitiennes

Forme hermitienne à gauche (resp. à droite) : c'est une forme sesquilinéaire à gauche (resp. à droite, suivant la convention choisie) sur E x E qui vérifie la propriété de symétrie hermitienne :

c) Pour tous x et y de E,

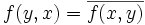
En particulier : , donc f(x,x) est un réel.

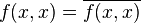
Réciproquement, une forme sesquilinéaire pour laquelle f(x,x) est réel pour tout vecteur x est nécessairement hermitienne.

Les formes hermitiennes (à gauche) constituent un espace vectoriel réel.

Forme hermitienne positive : c'est une forme hermitienne telle que :

d) pour tout x de E,

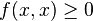
Forme hermitienne définie : c'est une forme hermitienne telle que

e) pour tout x de E, implique

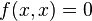
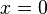
Forme hermitienne non dégénérée : c'est une forme hermitienne telle que :

f) pour tout x de E, si pour tout y de E, , alors

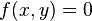
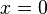
Toute forme hermitienne définie est donc non dégénérée. Pour une forme hermitienne positive, la réciproque est vraie grâce à l'inégalité de Cauchy-Schwarz : toute forme hermitienne positive non dégénérée est définie.

Une forme hermitienne définie positive (ou positive non dégénérée) est encore appelée produit scalaire (sous-entendu au sens complexe).