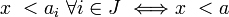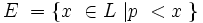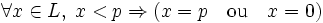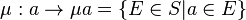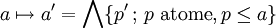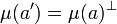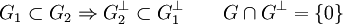Les trois axiomes de la mécanique quantique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Souvent, la mécanique quantique est présentée comme si elle était une théorie étrange, dépassant même l'entendement humain. Or s'il est vrai que cette théorie est très mal comprise par la plupart des profanes, elle est plutôt bien comprise par les initiés. Pourquoi une telle différence de compréhension ? Peut-être simplement car de nombreuses choses différentes ont été dites sur celle-ci, peut-être du fait que son formalisme est d'une abstraction jamais égalée auparavant par une théorie voulant décrire le "monde observable". Ou simplement car cette théorie va à l'encontre des fondements de la pensée scientifique, ceux-là même qui nous ont permis de construire notre représentation du monde. En effet la mécanique quantique pose de gros problèmes au concept du déterminisme tel que nous le connaissions avant le XXe siècle. Avec son avènement, il nous faut reconstruire les concepts de mesure, de reproductibilité d'une expérience, et même de déterminisme...
Le modèle des trois axiomes est une approche rigoureuse qui mène à l'idée que l'espace des états est un espace vectoriel (souvent un espace de Hilbert) chose qui est postulée par d'autres approches. La connaissance du théorème de Stone et du théorème de Noether (probablement les deux théorèmes les plus importants de la mécanique quantique, le premier servant à construire l'idée d'évolution temporelle, le deuxième la notion de quantité de mouvement) mène sans trop de difficulté à la reconstruction des postulats habituels de la mécanique quantique (voir postulats de la mécanique quantique).
Bibliographie
- Constantin Piron, Mécanique Quantique: Bases et Applications, Presses Polytechniques et Universitaires Romandes, 1998
- Cet ouvrage propose l'approche des « trois axiomes », mais ne parle pas des six postulats. Ce livre est donc plutôt destiné à des gens possédant déjà un bon niveau en mécanique quantique, malgré le fait qu'il soit mathématiquement accessible avec un niveau de mathématique de premier cycle universitaire.
Les 3 axiomes
Afin de posséder le vocabulaire des trois axiomes, il est nécessaire d'introduire quelques notions fondamentales. En effet, en opposé aux six postulats de la mécanique quantique, ces trois axiomes reposent sur des concepts étroitement liés à l'expérience voire à la mesure. (il peut être intéressant de lire Problème de la mesure quantique à ce sujet )
Questions, Propriétés et Espace des états
La notion de question découle de l'idée de mesure. Une question
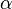
Pour illustrer cette idée, nous pouvons faire l'expérience de pensée suivante :
A partir de toute question
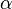
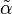
L'ensemble
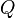
On dira qu'une question est vraie pour un système donné lorsqu'on peut prédire avec certitude (par un calcul théorique) que la mesure répondra "oui", avant de la réaliser. Une question non vraie n'est pas nécessairement fausse à coup sûr ; dans ce modèle on laisse la place aux questions incertaines, aléatoires. Une question est incertaine pour un système donné lorsque, si l'on construisait un système identique du point de vue de la physique, un clone possédant le même état physique, alors la mesure sur le clône ne donnerait pas à coup sûr la même valeur que la mesure sur le système d'origine. Une question incertaine ne peut par conséquent pas être vraie : le système physique choisit une réponse aléatoirement lorsqu'il est mesuré, malgré la connaissance totale de son état a priori. L'existence de questions incertaines est la différence clef entre la physique classique et la physique quantique, comme nous le formaliserons plus bas avec l'axiome 0.
On peut construire une relation de préordre partiel (relation d'ordre) sur les questions :
-
- Reprenons notre expérience de pensée, nous définissons deux questions :
-
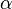
-
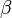
-
- On remarque que
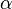
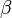
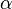
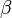
- Notation :
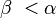
- Reprenons notre expérience de pensée, nous définissons deux questions :
Attention au sens, la question la plus faible est à droite de " < ". Cette notation est suggérée par le fait que l'ensemble des cas où
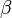
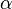
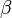
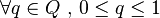
Ce préordre partiel crée une relation d'équivalence:
-
- on dira
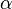
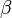
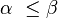
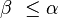
- notation :
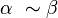
- on dira
La classe d'équivalence
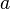
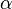
Une propriété est dite actuelle si les questions associées à celle-ci sont vraies à coup sûr. Au contraire, si les réponses à ses questions sont incertaines voire toujours fausses, on dit que la propriété est potentielle.
Nous définissons
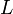
Une chose remarquable est, que sans aucune autre supposition, nous pouvons déjà avoir une certaine information sur la structure de
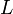
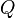
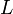
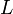
-
-
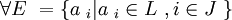
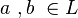
- si
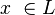
-
-
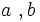
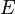
États et Propriétés-états
Par définition, l'état
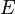
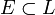
Un état
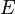
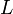
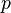
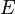
Une telle propriété
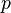
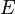
Atomes
Les atomes sont les éléments minimaux de
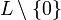
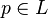
-
-
-
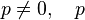
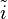
-
-
et que :
Les atomes sont des propriétés-états. En effet un atome
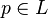
Représentation de Cartan
Par définition de la relation d'équivalence sous-jacente aux propriétés, une propriété est entièrement déterminée par les états du système dans lesquels elle est actuelle. On formalise cela ici, soit S l'ensemble de tous les états possible du système. Nous pouvons définir une application μ de L dans P(S) l'ensemble des partie de S.
Cette application s'appelle le morphisme de Cartan, et l'image de L dans P(S) est appelée la représentation de Cartan.
De plus, cette application est injective et préserve l'ordre et la borne inférieure.
Notion d'orthogonalité
On dit de deux états
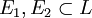
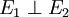
-
- α est vrai pour E1 et
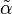
- α est vrai pour E1 et
Par exemple l'énergie d'une particule quantique piégée dans un puits de potentiel ne peut prendre qu'un ensemble discret de valeurs (elle est quantifiée). On peut donc définir deux états E1 et E2, où la particule quantique a respectivement une énergie e1 et e2. Ces 2 états sont orthogonaux par la question α = "la particule a une énergie e1", vraie dans l'état E1 et fausse dans l'état E2. Dans la représentation usuelle des états quantiques de la particule par un espace de Hilbert, les états E1 et E1 seront orthogonaux au sens du produit scalaire.
On dit que deux propriétés
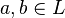
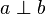
-
-
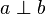
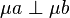
-
Système Classique
Axiome 0:
Nous dirons qu’une question
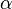
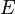
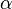
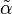
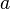
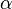
Cet axiome détermine entièrement la structure de
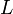
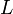
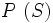
Généralisation : les systèmes quantiques
Axiome I
-
- Toute propriété-états est un atome de L
Cet axiome signifie simplement que si deux états
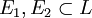
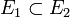
Aristote l'avait déjà énoncé : si le système change d’état, qu’il passe donc de l’état E1 à E2, il s’enrichit de nouvelles propriétés qui s’actualisent, et il en perd nécessairement d’autres. Donc E1 ne peut être entièrement contenu dans E2.
Cet axiome permet d'identifier les états du système aux atomes de L.
Axiome II
-
- Pour chaque état E donné il existe une (unique) question qui est vraie si et seulement si l’état du système est orthogonal à E
Pour chaque état E la question associée est bien unique, car définie par les états dans lesquels elle est actuelle : les états orthogonaux à E. Autrement dit pour n'importe quel état E, il existe une expérience physique permettant de savoir à coup sûr qu'un système donné est dans un état orthogonal à E.
En tenant compte de l'axiome I l'axiome II signifie que :
- Pour chaque propriété-état p atome de L, il existe une (unique) propriété p' qui est actuelle si et seulement si l’état est orthogonal à p
La fonction
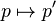
Cette fonction est plus claire dans la représentation de Cartan :
Notation :
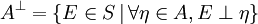
Axiome III
-
- L’application de L dans L :
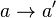
- L’application de L dans L :
Structure de l'espace des états
Tout comme l'axiome 0, les axiomes I, II, III déterminent entièrement la structure de l'espace des états.
Théorème :
- Si le système satisfait les axiomes 1, 2 et 3 alors:
-
- le morphisme de Cartan détermine un isomorphisme entre L et
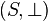
- L est un treillis complet, comblé d’atomes
- L’application définie dans l'axiome III est une orthocomplémentation
- le morphisme de Cartan détermine un isomorphisme entre L et
-
-
- L'espace des états est un treillis complet, comblé d’atomes et muni d’une orthocomplémentation
Les espaces de Hilbert
Nous désirons montrer que l’espace engendré par les rayons d’un espace de Hilbert convient parfaitement pour décrire un espace des états.
Théorème :
- Soit H un espace de Hilbert, l’ensemble de tous les sous-espaces G contenus dans H est un treillis complet, orthocomplémenté et comblé d’atome.
Démonstration :
-
-
- treillis complet :
- Les sous-espaces fermés G peuvent être ordonnés par inclusion. Ils forment un treillis complet car l’intersection d’ensembles fermés est encore un ensemble fermé.
- Orthocomplementé :
- l’application qui à G fait correspondre
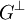
-
|
|
-
-
- Comblé d’atomes:
- Les atomes de ce treillis sont les sous-espaces de dimension 1 (c’est-à-dire les rayons) et tous les sous-espaces sont engendrés par les rayons qu’il contiennent.
-