Marin Ghetaldi - Définition

L'œuvre de Ghetaldi

L'œuvre de Ghetaldi s'étend dans de nombreuses directions.

Ghetaldi physicien

Le foyer du miroir parabolique

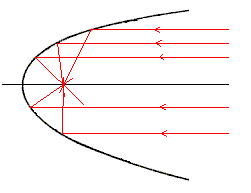
• En sciences physiques, on lui doit des expériences sur la densité des matériaux et la fabrication de verres teintés ; on retiendra son intérêt pour les miroirs et notamment les miroirs paraboliques, dont il décrit le foyer ; on lui doit aussi le calcul de densités, la mesure du rayon terrestre, et l'étude des ouvrages de fortification. Ses ouvrages étaient estimés et ses échelles des densités (publiées dans le Promotus Archimedes) furent souvent reprises, notamment par Gaspar Schott, qui les intégra telles quelles dans sa Magia universalis de 1658.

Ghetaldi mathématicien

• En mathématiques, l'œuvre de Ghetaldi est encore plus considérable. Élève de Michel Coignet et de Chrsitopher Clau, correspondant de Galileo Galilée et ami d'Alexander Anderson, il fut un émule patient d'Apollonius et rédigea deux livres à sa gloire. Mais surtout, il édita, popularisa et poursuivit l'œuvre de Viète, qu'il compléta par de nombreux ouvrages annonçant les découvertes de Pierre Fermat et de Girard Desargues.

• La plus importante contribution de Ghetaldi aux mathématiques est son application de l'algèbre à la géométrie, particulièrement dans son De resolutione et de compositione mathematica, libri quinque, publié à titre posthume par ses filles, Anna Francesca et Maria. Elles publièrent ce livre en respectant la volonté de leur père de le dédicacer au Cardinal Francesco Barberini. Il annonçait, sept ans avant la Géométrie du philosophe de la Haye et quatre ans avant Pierre Hérigone son mathematicus cursus. Cette publication est sans doute le premier livre de géométrie analytique jamais publié. Elle influença notamment Paolo Sarpi Antonio Santini, Jean de Beaugrand Giovanni Camillo Glorioso et Carlo Renaldini, l'un des derniers italiens à adopter le langage de l'algèbre nouvelle. Enfin, on retrouve des traces de ses travaux dans l'Opuscula mathematica de William Oughtred.

• A VOIR : La façon dont Ghetaldi écrit dans son De resolutione

Une œuvre en mouvement

Marino Ghetaldi in Galleria di ragusei illustri

Que ce soit par manque de temps, à cause de ses charges dans la république, ou à cause du peu d'importance qu'il attachait à délimiter le champ de ses propositions, les travaux de Ghetaldi ne sont pas exempts d'incorrections ou d'erreurs. De surcroît, il demeure prisonnier de la volonté de reconstruction des livres de l'Antiquité. Cette quête domine les mathématiques de la renaissance tardive (jusqu'à Hérigone), et Ghetaldi n'y échappe pas. Comme ses prédécesseurs, Francesco Maurolyco ou Marule, Viète, ou Snellius, Ghetaldi innove en croyant retrouver le véritable langage algébrique de Pappus, de Diophante, de Théon d'Alexandrie ou d'Apollonius de Perge. Il les dépasse toutefois et laisse entrevoir dans son dernier ouvrage, publié à titre posthume, les premiers développements de la géométrie analytique.

• Dans son De Variorum (1603), Ghetaldi résout trois sortes de problèmes par des méthodes purement géométriques. Il n'y donne pas toujours les conditions dans lesquelles s'appliquent ses résolutions, et c'est ce point que critiqua Clément Cyriaque de Mangin (mais aussi Jacob Christmann et ultérieurement Michelangelo Ricci), particulièrement la résolution d'un problème du à Regiomontanus : De triangulis planis et sphaerecis (1533). Alexander Anderson défendit l'honneur de l'école de François Viète (attaqué nommément par De Mangin), en publiant dès 1617 une réponse cinglante Animadversionis in Francisum Vietam puis compléta la résolution en 1619 dans Exercitationum mathematicorum decas primas ; Ghetaldi revint sur ce défaut dans son dernier ouvrage.

• Dans Nonnullae propositiones de parabola, Ghetaldi ne parvint pas non plus à démontrer parfaitement l'identité des paraboles obtenues par section d'un cône oblique et celles obtenues par section d'un cône de révolution.

• Plus tard, dans Supplementum Apollonii Galli, il ne résout qu'imparfaitement le cinquième problème d'Apollonios, provoquant la publication en 1612 par Alexander Anderson de son Supplementum Apollonii redivi. Le traité de l'Ecossais fut alors apporté à Raguse par l'orientaliste George Strachan et donna lieu a une correction de Ghetaldi en 1613 dans son Apollonius redivivus seu restitutae Apollonü Pergaei de inclinationibus geometriae, liber secundus. Quoique leurs méthodes de résolution de ce cinquième problème d'Apollonius soient différentes, Ghetaldi marque dans sa préface tout le respect qu'il doit aux travaux de l'Écossais. Anderson de son côté, dédicacera à Ghetaldi la publication en 1615 de ses Zététiques des problèmes d'Apollonius.
• On retrouve encore la volonté de résoudre cette difficile question dans le dernier ouvrage de Ghetaldi : le De resolutione et de compositione mathematica, libri quinque, qui s'ouvre par la liste des propositions qui y sont démontrées, et donne des solutions algébriques à des problèmes d'Apollonius de Perge que Ghetaldi a déjà résolus géométriquement (mais sans préciser les conditions limites des grandeurs en jeu) dans ses premières publications. Cette œuvre a fait l'objet d'études approfondies par Eugène Gelcich en 1882. Il y reprend notamment le cinquième problème d'Apollonius par les méthodes de l'Algèbre nouvelle. On a remarqué qu'il n'y cite pas les travaux qu'Anderson à consacré à ce sujet en 1619, sans doute faute de ne pas les avoir reçus.

Publications

On connait sept livres de Ghetaldi  :

• Promotus Archimedus sev De varijs corporum generibus grauitate & magnitudine comparatis (1603) Rome ; disponible aussi sur Google livres (voir page 21)
• Nonnullae propositiones de parabola (1603) Rome disponible sur Google livres page 1
• Variorum problematum colletio , (1607) Venise, pamphlet contenant 42 problèmes mathématiques ; dédicacé à Marino Gozzi.
• Apollonius redivivus seu restituta Apollonii Pergaei inclinationum geometria (1607)
• Supplementum Apollonii Galli (1612)
• Apollonius redivivus seu restitutae Apollonü Pergaei de inclinationibus geometriae, liber secundus (1613) Liber I. et II. Cum suppl, Volume 2 apud Baretium à Venise.
• De resolutione et compositione mathematica posthume (1630) ou ici sur Google.fr

On lui doit également la construction d'un miroir parabolique conservé jusqu'au XIXe siècle dans les collections de la famille Barbarini, puis au musée maritime de Londres ainsi qu'en 1604 la construction d'une tour Pozvizd, faisant partie du système de fortification de Raguse.

Retentissement

Le blason de la famille Ghetaldi

Ghetaldi fut reconnu très tôt comme un des meilleurs géomètres et algébristes de son temps. Dès 1603, Henry Percy, le protecteur de Thomas Harriot et neuvième comte de Northumberland a entendu parler de lui. Une certaine concurrence s'établit d'ailleurs autour d'Harriot à propos des mesures des densités. En France, moins de quatre ans après sa disparition, Pierre Hérigone précise, à la fin du premier volume de son Cursus Mathematicus, qu'il lui doit certaines de ses propositions. Quant à Johannes Kepler, il le prisait, selon ses lettres, comme l'égal de Galilée. Il fut également apprécié par Mersenne et Claude Mydorge

Au dix-septième siècle, les travaux de Marino Ghetaldi furent tenus en grande estime par de nombreux savants, notamment l'anglais Edmond Halley et le hollandais Christian Huygens. A la fin du siècle, Montucla le cite encore dans son histoire, mais donne à Descartes toute la gloire de l'invention de la géométrie analytique. Au siècle suivant, Charles Bossut et Joseph-Louis Lagrange l'ont quasiment rayé de leur histoire des sciences. Les allemands lui rendirent souvent un juste hommage, notamment Abraham Gotthelf Kästner. En fait, son influence se maintint au XVIII^e siècle par l'entremise des anglais, John Lawson, Samuel Horsley, Reuben Burrow qui empruntèrent encore beaucoup à ses travaux. Ils furent suivis au siècle suivant par Johann Wilhelm Von Camerer (1763-1847) et Daniel Schwenter.

Au XIX^e siècle, Michel Chasles semble ignorer son importance et n'en parle qu'incidemment en marge de Viète. Francesco Maria Appendini puis G. Barbieri lui rendent un hommage en 1802 puis 1840, dans leurs Galleries de Ragusiens illustres. Ils sont suivis 16 ans plus tard par Simeone Gliubich. En 1868, l'éditeur de la Penny encyclopédie, Charles Knight, lui consacre quelques pages dans ses biographies mais il faudra attendre la fin du dix-neuvième siècle, Antonio Favaro, Heinrich. Wieleitner (1874-1931) et Eugène Gelcich (un professeur à l'école navale de Pola, en Autriche) pour que son importance soit pleinement reconnu. Pour autant, ses œuvres n'ont toujours pas été traduites du latin.

Michael Sean Mahoney a évoqué dans The begenings of algebra thought l'importance du De resolutione et compositione mathematica ; il lui rend un vibrant hommage dans The mathematical career of Pierre de Fermat, 1601-1665, précisant quels soins Ghetaldi mettait à accomplir les étapes zététique et poristique des problèmes géométriques qu'il avait en vue, mais aussi qu'il suivait dans leur exégèse, les étapes de la poristique. Plus récemment, son œuvre a été entièrement rééditée, et commentée, par l'astronome croate Zarko Dadic

Dans sa patrie, la renommée de Marin Ghétaldi fut longtemps à l'honneur ; au XIX^e, on donna encore son nom à un navire. La grotte située au pied du mont Bergato, dans la quelle il travaillait à ses expériences d'optique lui conféra la réputation d'un ermite et d'un mage, et le surnom de bête auprès des populations locales.

Cette grotte de Raguse, où il menait ses expériences sur les miroirs, et reliée à sa villa selon l'écrivain Andrew Archibald Paton, porte désormais son malheureux surnom.