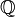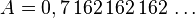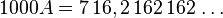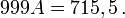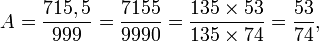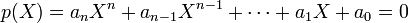Nombre irrationnel - Définition

Développements décimaux

Le développement décimal d'un nombre irrationnel ne se répète jamais et ne se termine jamais. Le développement décimal d'un nombre rationnel se finit ou se répète.

Pour le démontrer, soit un nombre rationnel c'est-à-dire supposons que l'on divise deux entiers n par m (m étant non nul) ; alors lorsque l'algorithme de division euclidienne enseigné à l'école primaire est utilisé pour diviser n par m, il ne peut donner que m restes différents. Si 0 n'apparaît jamais comme reste, alors l'algorithme ne peut effectuer plus de m − 1 étapes sans redonner un même reste. Après cela, si un reste réapparaît, alors le développement décimal se répète!

Inversement, supposons qu'il y ait dans le développement d'un nombre des décimales récurrentes ; on peut alors démontrer que le nombre est une fraction de deux entiers. Par exemple :

Dans ce développement, la longueur de la séquence de décimales répétées est égale à 3. Multiplions par 10³:

Remarquez que puisque nous avons multiplié par 10³ la longueur de la période, nous avons décalé des chiffres vers la gauche par rapport à la virgule d'autant de positions.

Nous remarquons alors que les décimales de 1000A et de A à partir d'une certaine position sont identiques. Ainsi dans l'écriture décimale de 1000A et de A la séquence 162 se répète à partir d'un certain rang.

Par conséquent, lorsque nous soustrayons A à 1000A, les décimales de la différence deviennent nulles à partir de ce rang.

Ainsi

qui est un quotient de nombres entiers et apparaît donc comme un nombre rationnel.

Nombres irrationnels transcendants et algébriques

Presque tous les nombres irrationnels sont transcendants et tous les nombres transcendants sont irrationnels. Donnons comme exemples de nombres transcendants les nombres e^r et π^r qui sont irrationnels si est rationnel ; e est aussi irrationnel.

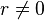
Un autre moyen de construire des nombres irrationnels considère les nombres algébriques irrationnels, c'est-à-dire des racines de polynômes à coefficients entiers. Considérons une équation algébrique de la forme

où les coefficients a_i sont entiers.

Supposons qu'il existe un réel x tel que p(x) = 0 (par exemple si n est impair et a_n est non nul, un tel x existe d'après le théorème des valeurs intermédiaires).

Les seules racines rationnelles de cette équation algébrique sont de la forme r / s d'une fraction irréductible où r est diviseur de a₀ et s un diviseur de a_n ; il y a seulement un nombre fini de valeurs possibles que l'on peut essayer à la main. Si aucune de ces valeurs n'est racine de p, x doit être irrationnel. Par exemple, si nous avons (X³ − 1)² = 2 alors X⁶ − 2X³ − 1 = 0 et le polynôme X⁶ − 2X³ − 1 n'a pas de racine rationnelle (les seules valeurs possibles étant ).

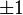
Parce que les nombres algébriques forment un corps, beaucoup de nombres irrationnels peuvent être construits en combinant les nombres algébriques et les nombres transcendants. Par exemple 3π + 2, et sont irrationnels et même transcendants.

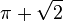
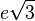
L'ensemble des irrationnels

L'ensemble des nombres irrationnels est indénombrable (puisque l'ensemble des rationnels est dénombrable et que celui des nombres réels ne l'est pas). L'ensemble des nombres irrationnels algébriques, c'est-à-dire des irrationnels non transcendants, est dénombrable. Avec la valeur absolue comme distance, l'ensemble des nombres irrationnels devient un espace métrique qui n'est pas complet. Cependant, cet espace métrique est homéomorphe à l'espace métrique complet de toutes les suites entières positives ; l'homéomorphisme est donné par le développement en fraction continue. Ceci démontre que le théorème de catégorie de Baire s'applique aussi à l'espace des nombres irrationnels. Alors que l'ensemble des nombres réels muni de sa topologie usuelle est connexe, cet espace de Baire, devient un espace topologique comme celui des réels, à savoir avec la topologie de l'ordre, mais totalement non connexe puisqu'il n'existe aucun chemin joignant deux irrationnels distincts restant sur la droite des irrationnels. L'ensemble des irrationnels, tout comme l'ensemble des rationnels, est dense dans l'ensemble des réels.