Palimpseste d'Archimède - Définition

Introduction

Une page typique du palimpseste d'Archimède. Le manuscrit original du texte d'Archimède est écrit de droite à gauche, dissimulé sous le texte de prières écrites de haut en bas

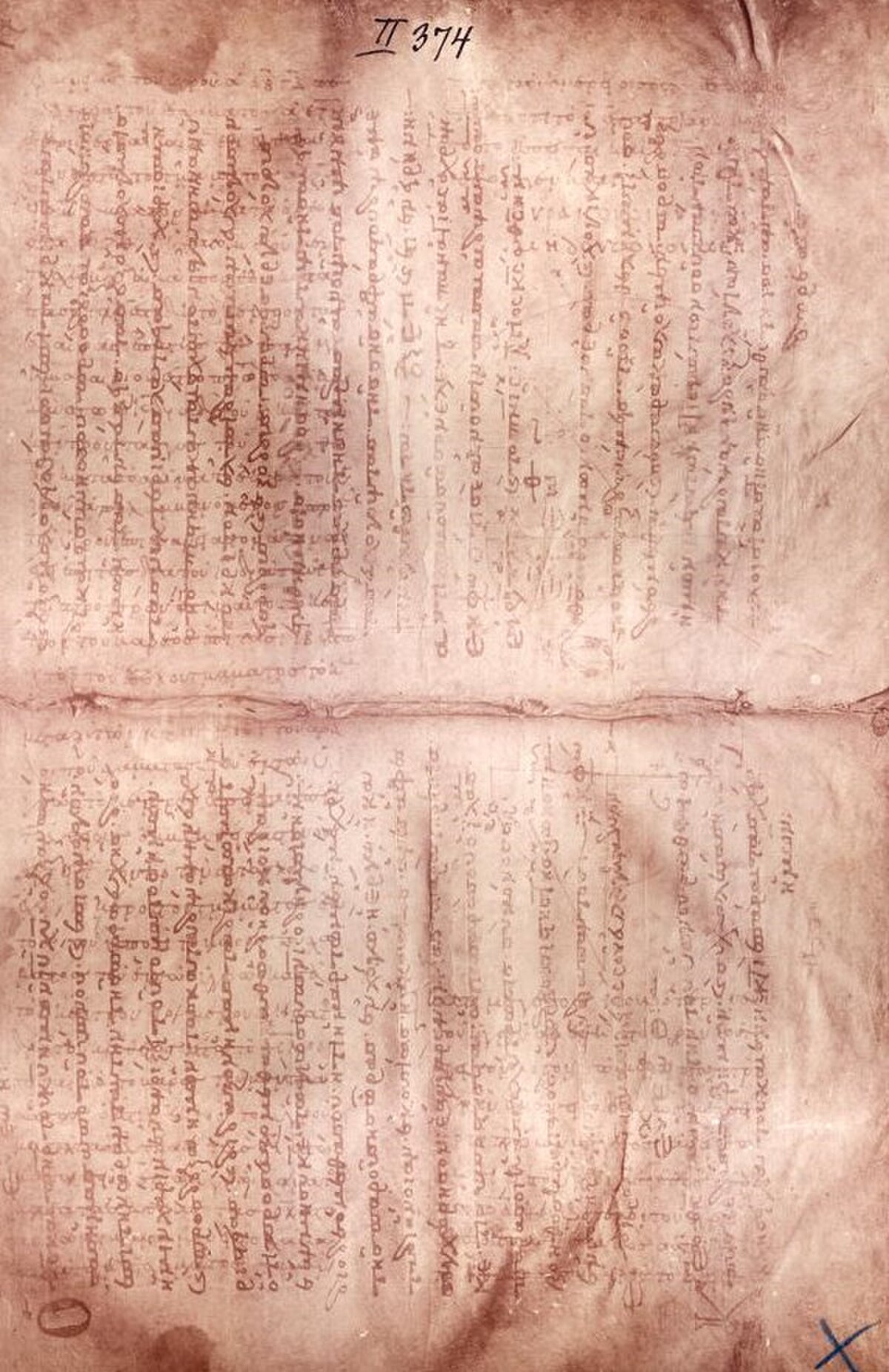
Le Palimpseste d'Archimède est une des plus anciennes copies d'un ouvrage écrit par le mathématicien, physicien et ingénieur grec, Archimède de Syracuse (287 av. J.-C. - 212 av. J.-C.). Un palimpseste, est un manuscrit écrit sur un parchemin usagé, dont les caractères ont été effacés afin de pouvoir réutiliser le parchemin, qui était rare et coûtait cher à l'époque. Le texte originel d'Archimède (qui a vécu au IIIe siècle avant JC), recopié au X^e siècle, a ainsi été gratté par un prêtre qui a réécrit par dessus un livre liturgique grec, dans la seconde moitié du XII^e siècle ou dans la première moitié du XIII^e siècle.

Le Palimpseste d'Archimède est relié sous la forme d'un codex. C'était un livre d'environ 90 pages, avant d'être transformé en un palimpseste de 177 pages. Heureusement, l'effacement du texte original fut incomplet, et on peut encore le lire grâce à des ultraviolets, rayon X et à la simple lumière.

Il fut découvert à Constantinople en 1906 et publié à partir de photographies par le philologue danois Johan Ludvig Heiberg (1854-1928) ; puis traduit du grec en anglais par Thomas Heath. Parmi les textes d'Archimède contenus dans l'ouvrage, ceci permit à la communauté scientifique d'en découvrir certains restés inédits jusque là :

• De l’équilibre des figures planes
• Des spirales.
• De la mesure du cercle.
• De la sphère et du cylindre
• Des corps flottants (seule copie connue en grec)
• De la méthode (seule copie connue)
• Stomachion (seule copie connue)

Le palimpseste contient également des discours du politicien du IVe siècle avant JC, Hypéride, et un commentaire sur les Catégories d'Aristote par Alexandre d'Aphrodisie.

Contenu mathématique

La méthode

Le contenu le plus remarquable de ce palimpseste est le traité d'Archimède La méthode dont c'est la seule copie connue. Ce traité donne des indications précieuses sur une méthode utilisée par Archimède pour déterminer certaines mesures d'aire ou de volume, par exemple l'aire d'un segment de parabole ou le volume d'une boule. Outre ces deux résultats, on y trouve également le calcul du centre de gravité d'une demi-sphère, et celui d'un tronc de paraboloïde.

Des démonstrations géométriques de formule d'aire ou de volume sont connues depuis l'Antiquité et reposent sur un double raisonnement par l'absurde appelé méthode d'exhaustion : pour prouver que deux quantités sont égales, on suppose que la première est plus grande que la seconde et on démontre que cela conduit à une contradiction, puis on suppose que la seconde est plus grande que la première pour arriver à une autre contradiction. On en déduit alors l'égalité des deux quantités. Ces raisonnements reposent généralement sur des encadrements de la figure par des figures quarrables de plus en plus précises (voir quadrature de la parabole). La méthode par exhaustion nécessite cependant de connaître a priori le résultat final. Par exemple, on ne calcule pas l'aire du segment de parabole ; on prouve que cette aire est égale à 4/3 de l'aire d'un certain triangle inscrit dans ce segment. De même, on ne calcule pas le volume de la boule ; on prouve que ce volume est le quadruple du volume d'un cône de base égale à un grand cercle de la boule et de hauteur égale au rayon de la boule. Mais on ignorait comment Archimède était parvenu à deviner quelles étaient les formules à prouver. L'explication figure dans La méthode.

Dans ce traité, Archimède utilise des méthodes mécaniques par pesées, en découpant les surfaces ou les volumes considérés en tranches (voir quadrature par la méthode des pesées). Sa démarche, remarquable par l'utilisation unique à l'époque qu'il fait de l'infini, utilise des techniques très proches de celles qui seront réinventées au XVIIème siècle, en particulier la méthode des indivisibles de Cavalieri, précurseur du calcul intégral de Newton et Leibniz. Aucun de ces auteurs n'avaient connaissance de la Méthode utilisée par Archimède.

Quelques pages de La Méthode n'ont pas été utilisées par l'auteur du palimpseste et sont donc définitivement perdues, comme le calcul du volume de l'intersection de deux cylindres.

Le Stomachion

Le Stomachion est un problème de puzzle présent dans le palimpseste d'Archimède

Le palimpseste fournit aussi un exemplaire de Stomachion : ce problème se présente comme un puzzle à reconstituer. Analogue au tangram, il est composé de 14 pièces (contre 7 pour le tangram). Le document concernant le Stomachion est très incomplet mais Archimède semble donner la méthode de construction de celui-ci et les rapports des angles des différentes pièces ainsi que leurs aires. Reviel Netz de l'université Stanford pense que la réflexion d'Archimède portait sur le nombre de façons de reconstituer celui-ci. Les calculs sur les combinaisons mènent à 17 152 combinaisons possibles, dont 536, différentes à une isométrie près, permettant de reconstituer le carré. Le document présent sur le palimpseste est trop incomplet pour que l'on puisse savoir si Archimède a abouti au même résultat. Ce travail serait alors l'utilisation la plus élaborée de la combinatoire dans l'antiquité grecque.