Pelote aléatoire - Définition

Polymères réels

Un polymère réel n'est pas « librement »-joint, c'est-à-dire que ses liaisons imposent des contraintes sur leurs voisinages respectifs. Une liaison chimique simple C-C constitue un angle tétraédrique de l'ordre de 109,5 degrés, par exemple, dans un alcane. La valeur de L est bien définie pour, par exemple, un polyéthylène ou un polyamide complètement étiré, mais est inférieur à N x l en raison du squelette non linéaire (zig-zag). Il y a cependant une rotation libre pour de nombreuses liaisons de la chaîne. Le modèle ci-dessus peut être amélioré. Une longueur « effective » unité plus importante peut être définie de façon à ce que la chaîne soit définie comme liée librement, avec un N plus petit, de telle façon à ce que la contrainte L = N x l soit respectée. Ceci donne aussi une distribution gaussienne. Cependant, des cas spécifiques peuvent être aussi calculés précisément. La distance moyenne de terminaison à terminaison pour le polyméthylène (polyéthylène avec chaque -C-C- considéré comme une sous-unité) à rotation libre (mais non librement lié) est l fois la racine carrée de 2 N, soit une augmentation de taille par un facteur 1,4 environ. Contrairement au volume nul postulé dans une marche aléatoire, tous les segments de polymères réels occupant de l'espace en raison des rayons de van der Waals des atomes constitutifs, y compris les groupes substituants interférant avec les rotations de liaisons. Cela peut aussi être pris en compte dans les calculs. Ces effets accroissent la distance de terminaison à terminaison moyenne.

Leurs polymérisations étant un processus stochastique, les chaînes polymères dans toute population de polymères synthétiques auront des longueurs statistiquement distribuées. Dans ce cas, N sera considéré comme une valeur moyenne. De plus, de nombreux polymères ont des ramifications aléatoires.

Même avec des corrections pour les contraintes locales, le modèle de marche aléatoire ignore les interférences stériques entre chaînes, et entre des parties distinctes d'une même chaîne. Une chaîne peut parfois ne pas sortir d'une conformation précise pour aller vers une conformation proche par un petit déplacement car une de ses parties devra passer au travers d'une autre, ou au travers d'un voisin. On pourra seulement indiquer que le modèle de pelote aléatoire par chaîne idéale est pour le moins une indication qualitative des formes et dimensions des polymères réels en solution, et, pour l'état amorphe, aussi longtemps qu'il n'existe que de faibles interactions physicochimiques entre monomères. Ce modèle, et la théorie de la solution de Flory-Huggins, pour laquelle Paul Flory reçut le prix Nobel de chimie en 1974, s'appliquent essentiellement aux solutions idéales donc diluées. Mais il existe des raisons de penser (par exemple par des études en diffraction de neutrons) que les effets stériques peuvent disparaître, c'est-à-dire que sous certaines conditions, les dimensions de chaînes des polymères amorphes ont approximativement la taille idéale calculée.

Quand des chaînes séparées interagissent, notamment dans la formation de régions cristalline des thermoplastiques solides, une approche mathématique différente doit être utilisée.

Des polymères plus rigides tels les polypeptides hélicoïdaux, le Kevlar ou la double chaîne d'ADN peuvent être gérés par le modèle du ver (en).

Modèle de chemin aléatoire : chaîne gaussienne

Chaîne aléatoire courte

Il existe un nombre considérable de manières possibles pour une chaîne de se replier sous forme relativement compacte, comme une pelote de ficelle avec de nombreux espaces vides, et comparativement beaucoup moins pour qu'elle soit plus ou moins étirée. Ainsi si chaque conformation est de probabilité égale ou possède un même poids statistique, les chaînes seront plus probablement en forme de boules qu'étendues - par effet purement entropique. La plupart des chaînes d'un ensemble seront donc repliées de manière compacte. Ou de manière réciproque, c'est la conformation qu'adoptera n'importe laquelle d'entre elles la plupart du temps.
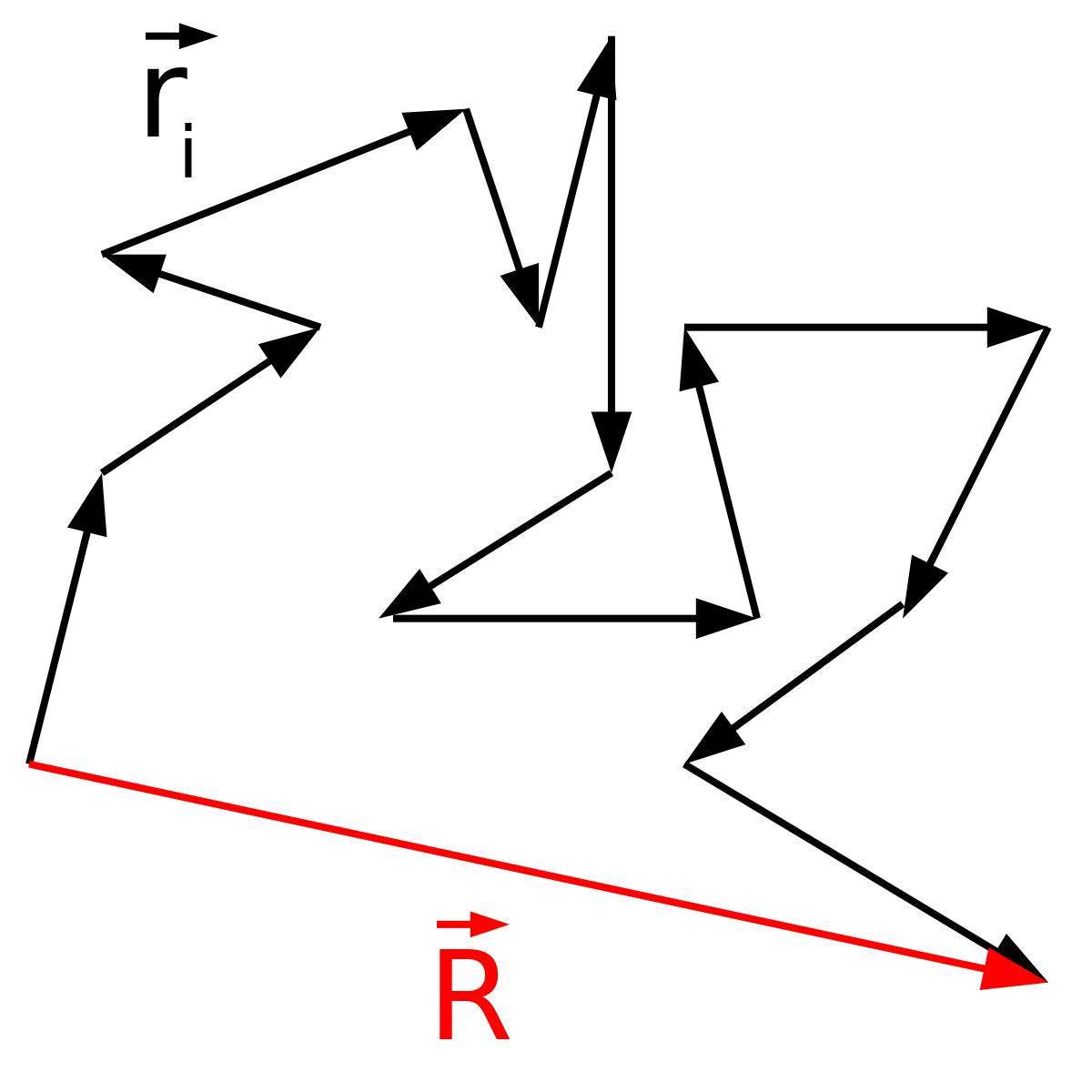
Considérons un polymère linéaire comme étant une chaîne librement constitutée de N sous-unités, chacune de longueur l, occupant un volume nul, aucune partie de la chaîne ne pouvant donc exclure une autre de n'importe quel localisation. On peut considérer les segments de chacune de ce type de chaîne comme un ensemble défini par une marche aléatoire (ou « vol aléatoire ») en trois dimensions, limité seulement par la contrainte que chaque segment doit être joint à ses voisins. Ceci constitue le modèle mathématique de chaîne aléatoire. La longueur maximale L de cette chaîne est évidemment N x l. Si l'on considère que chaque conformation de chaîne possible possède un poids statistique identique, on peut démontrer que la probabilité P(r) d'une chaîne polymère dans la conformation permettant d'avoir une distance r entre les terminaisons obéira à la loi de distribution décrite par la formule :

La distance moyenne (valeur efficace) entre les terminaisons de la chaîne, , tend à être l fois la racine carrée de N - soit en d'autres termes, la distance moyenne croît en N^{1 / 2}.
Bien que ce modèle soit appelé « chaîne gaussienne », la fonction de distribution ne suit pas une loi normale gaussienne. La fonction de distribution de probabilité pour la distance de terminaison à terminaison d'une chaîne gaussienne est non nulle seulement pour r > 0.