Photogrammétrie - Définition

Introduction

La photogrammétrie est une technique qui consiste à effectuer des mesures dans une scène, en utilisant la parallaxe obtenue entre des images acquises selon des points de vue différents. Recopiant la vision stéréoscopique humaine, elle a longtemps exploité celle-ci pour reconstituer le relief de la scène à partir de cette différence de points de vue. Actuellement, elle exploite de plus en plus les calculs de corrélation entre des images désormais numériques. Cette technique repose entièrement sur une modélisation rigoureuse de la géométrie des images et de leur acquisition afin de reconstituer une copie 3D exacte de la réalité.

Histoire

La photogrammétrie a fortement évolué depuis sa première application réalisée par un officier de l’armée française, Aimé Laussedat en 1849 sur la façade de l'Hôtel des Invalides : il a eu en effet l’idée d’utiliser des photographies de paysages non seulement pour observer le terrain mais aussi pour le mesurer. Il met ainsi au point une technique qui s’appellera plus tard la photogrammétrie. Laussedat devient professeur au CNAM en 1873, titulaire de la chaire de géométrie appliquée aux arts où il est souvent question de topographie, et celui que l’on peut considérer comme l’inventeur de la photogrammétrie sera même directeur du Conservatoire de 1881 à 1900. L'autre personnage-clé est Félix Tournachon, plus connu sous le nom de Nadar, qui dans les années 1860 monte en ballon pour photographier Paris et bien d'autres villes, et qui a très bien compris, à en juger par les brevets qu’il a déposés, l’intérêt de la photographie aérienne pour des finalités tant civiles que militaires. Inventée en France, la photogrammétrie a ensuite été développée et industrialisée de façon très complète en Allemagne. En pratique, il faut attendre l’entre-deux-guerres pour que la photographie aérienne se généralise, avec le développement de l’aviation. Après-guerre, on observe un emploi de plus en plus systématique de la photogrammétrie pour réaliser les cartes de base de pays entiers. Les développements de l'imagerie spatiale à haute résolution et de la puissance de l'informatique grand public ont donné depuis peu de nouvelles impulsions à ce domaine. Mais en parallèle, les développements au sein de la communauté de vision par ordinateur, destinés essentiellement à des applications de robotique, ont capitalisé depuis une décennie l'essentiel des efforts de recherche dans ce même domaine. C'est cette communauté qui, actuellement, est principalement porteuse de l'avenir de la photogrammétrie.

Bases géométriques

Suite des opérations menées pour mettre en place un couple stéréoscopique (selon D. Moisset, IGN).

Figure de base de la géométrie stéréoscopique.

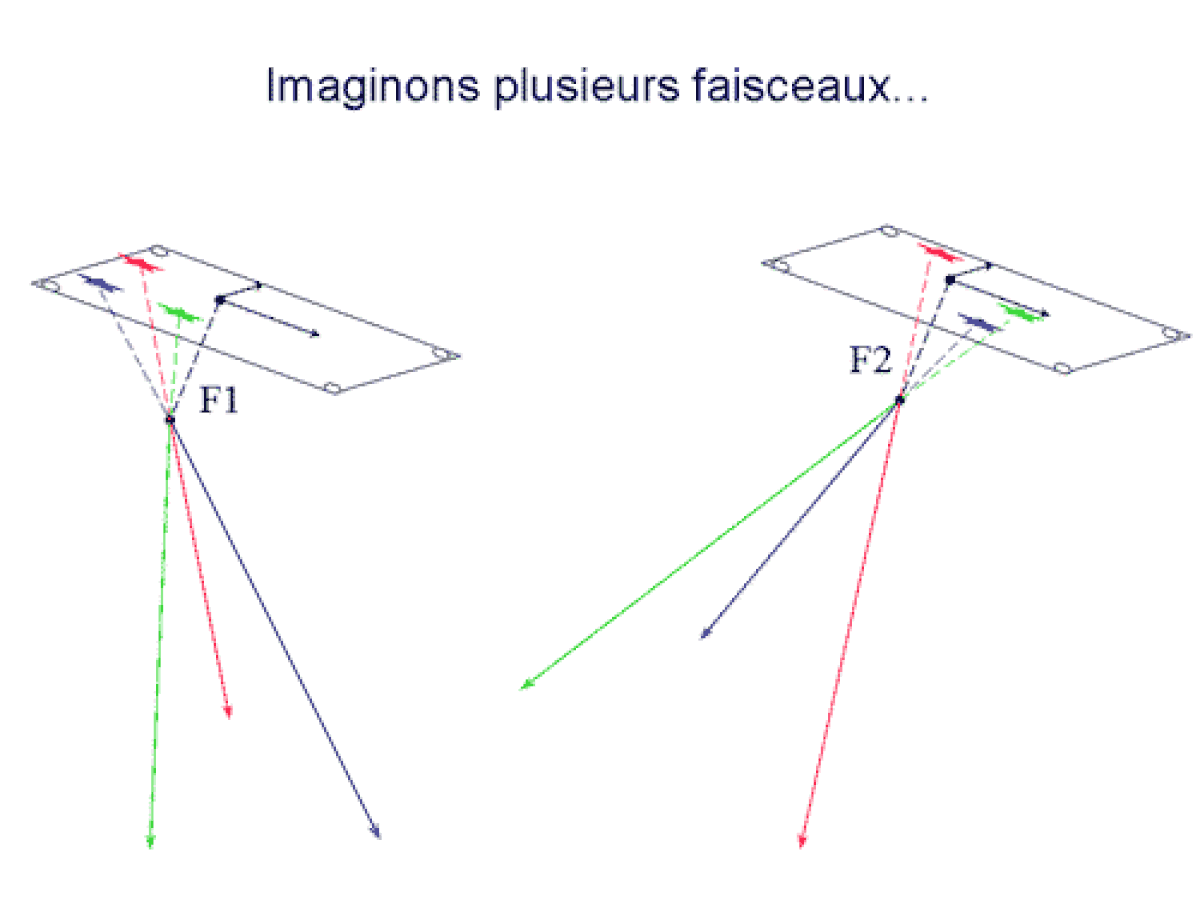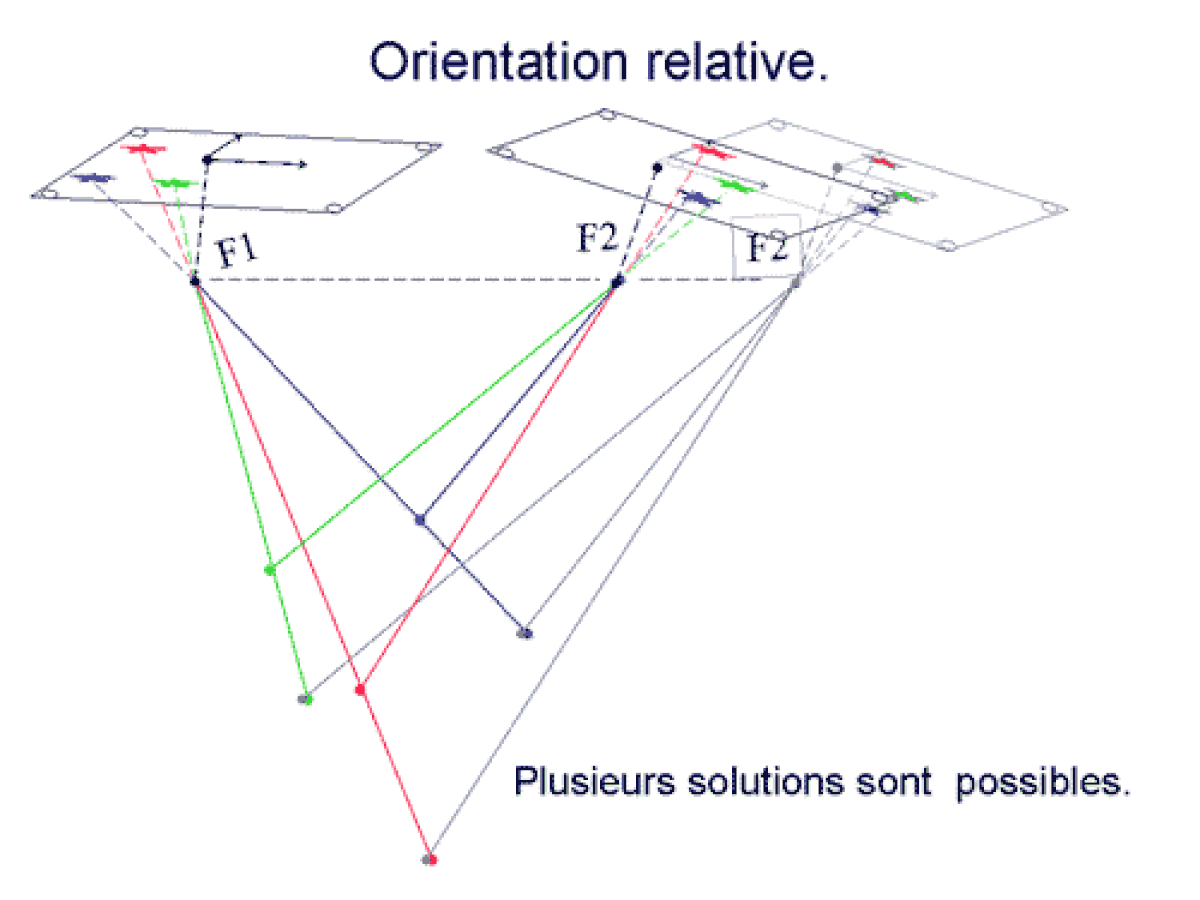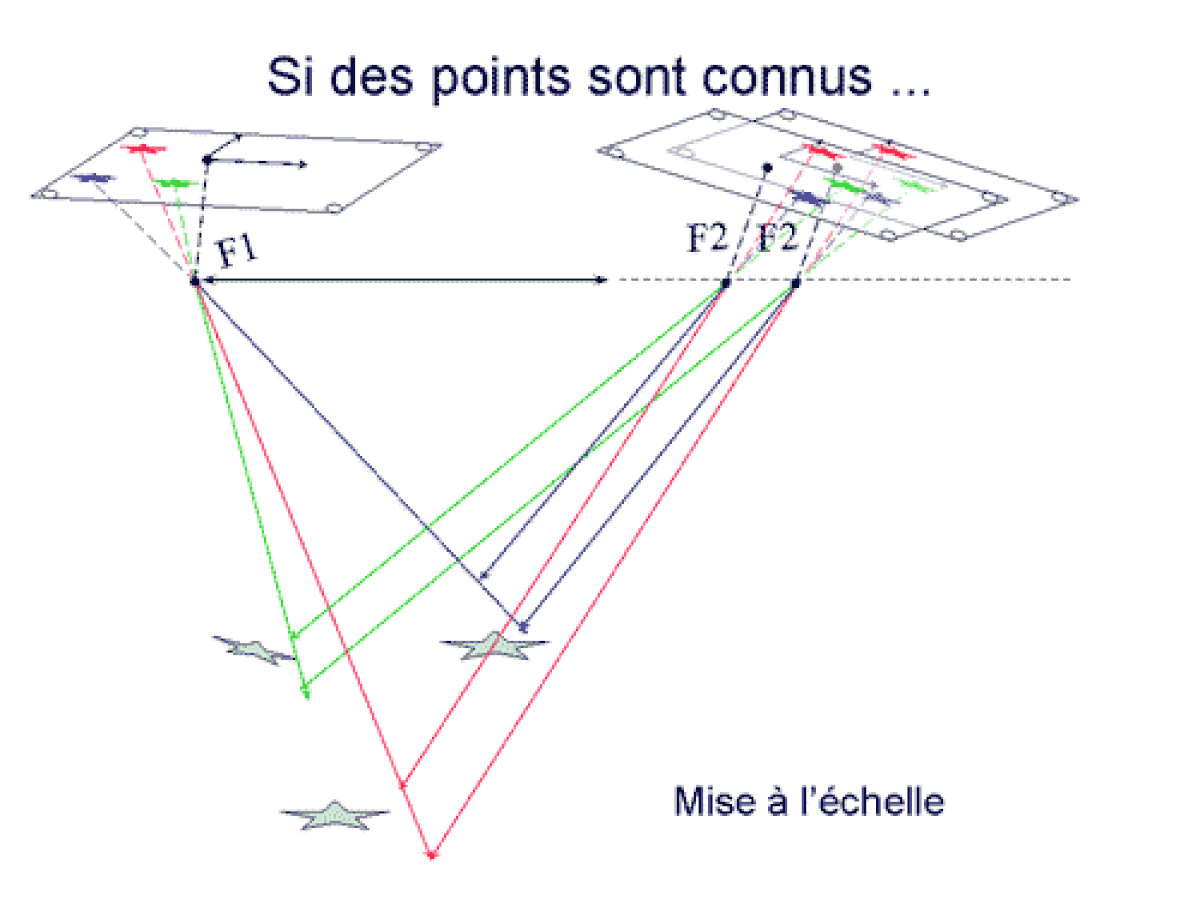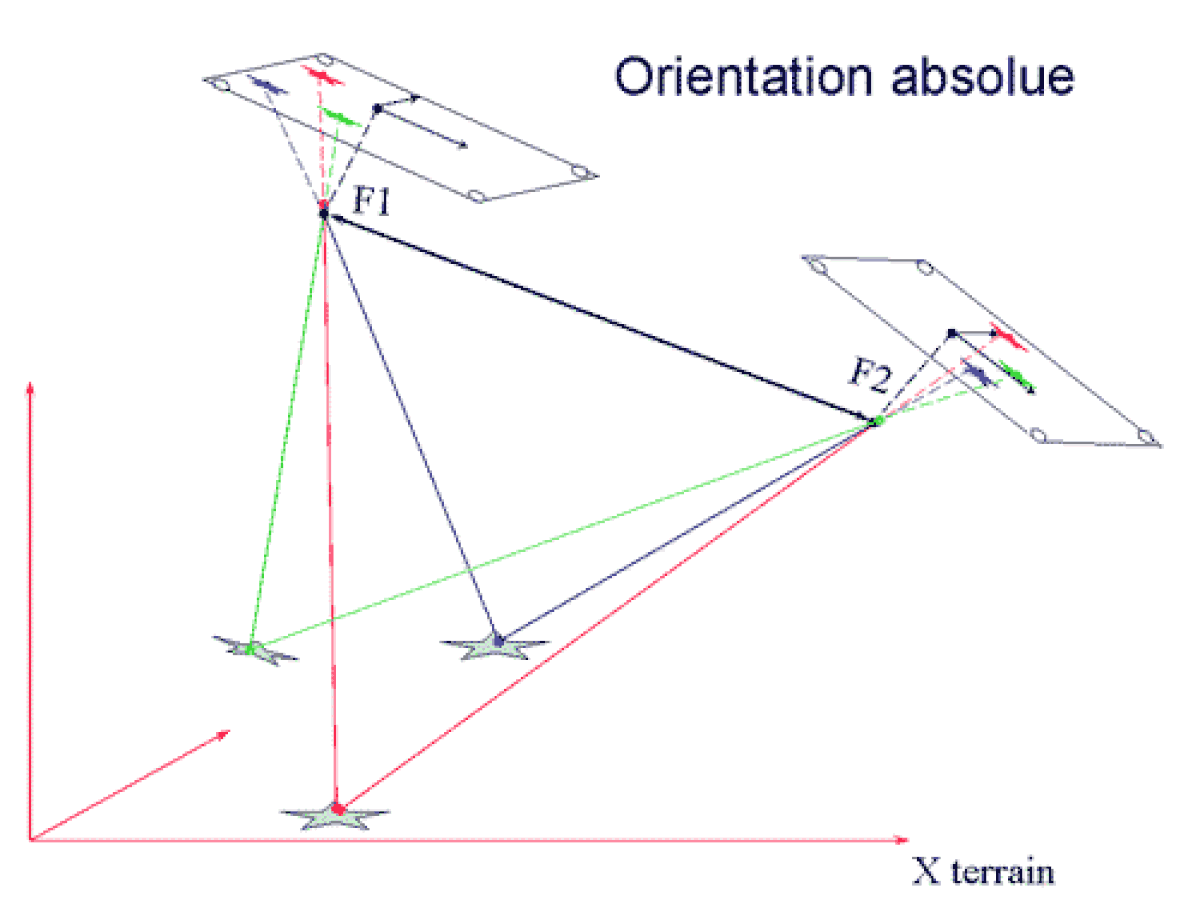
La formalisation géométrique de la stéréoscopie repose sur deux types d'équations, tous deux largement utilisés en photogrammétrie et en vision par ordinateur, le but étant de déterminer l'orientation relative des images à partir des points identifiés comme homologues dans deux images :

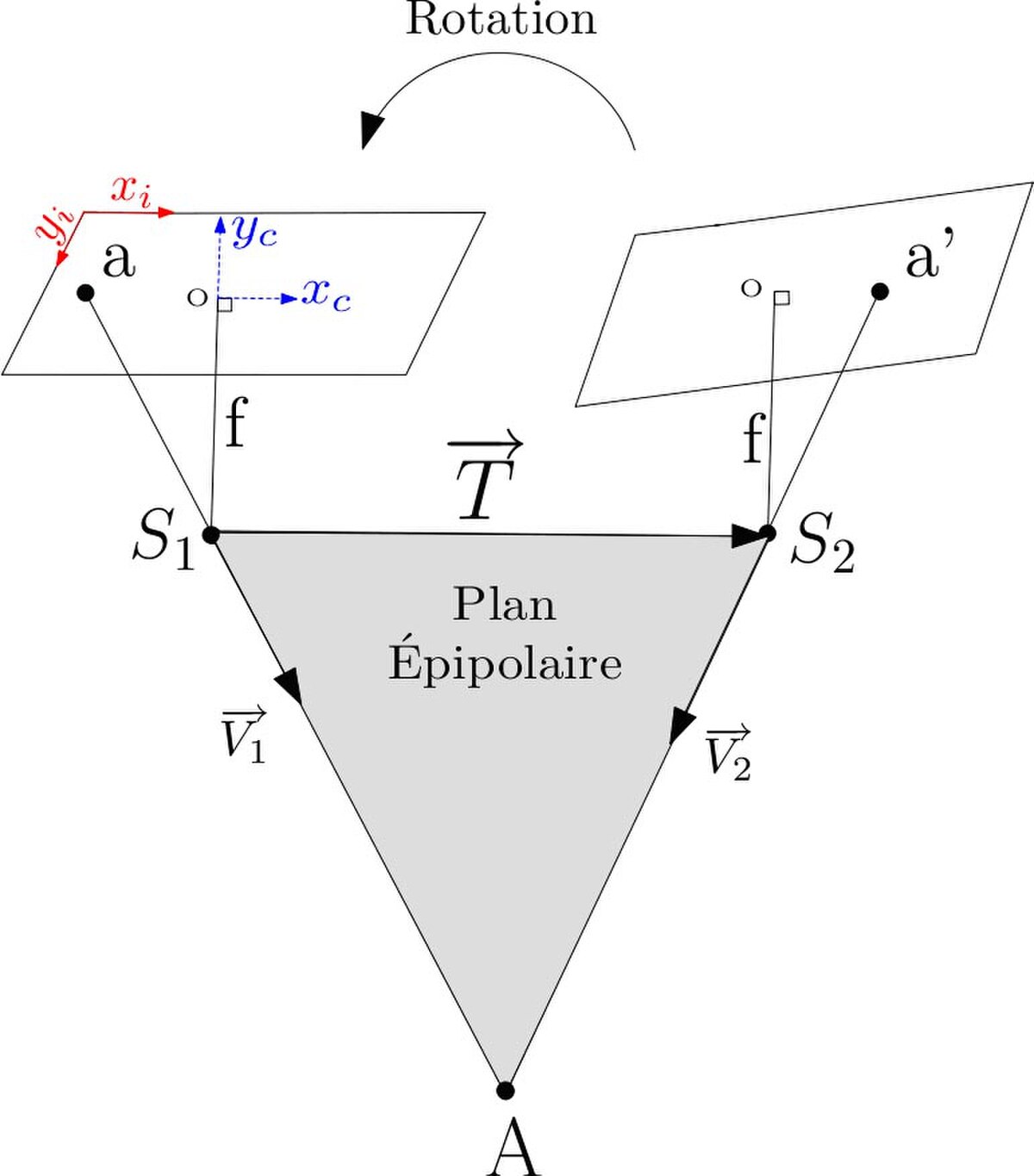
• L'équation de colinéarité. a et a' étant les images du point A de l'espace réel dans deux plans images (correspondant à deux positions successives du plan focal d'une caméra donnée), on écrit simplement le fait que a, S₁ et A sont alignés, ainsi que a', S₂ et A. Ces expressions ne sont rigoureusement exactes que si les optiques employées sont dépourvues de distorsion (ou corrigées de celle-ci). Cette approche est historiquement celle qui a été utilisée en photogrammétrie, son principal inconvénient résulte du fait que le problème de l'orientation relative de deux images est ici non linéaire, et exige donc une solution approchée pour démarrer les calculs. Cette solution approchée est simple en photogrammétrie aérienne, car les axes de prises de vues sont quasiment verticaux, les images étant sensiblement orientées de façon similaire. La démarche consiste donc à calculer l'orientation relative des images, puis à mettre l'objet 3D ainsi obtenu à sa place dans l'espace (orientation absolue), et enfin le mettre à l'échelle.

• L'équation de coplanarité. L'approche est un peu différente, même si elle est géométriquement équivalente, on écrit que les vecteurs , et sont coplanaires. Cette méthode est la base de la résolution de l'orientation relative au sein de la communauté de la vision par ordinateur. Les trois vecteurs étant coplanaires, on exprime que leur produit mixte est nul, ce qui peut s'écrire comme une forme quadratique basée sur une matrice, appelée "matrice essentielle" (terme consacré). Cette matrice résulte du produit de l'axiateur formé à partir de la translation avec la matrice de rotation permettant de passer du référentiel de l'image 2 à celui de l'image 1. Cette approche suppose la connaissance préalable des paramètres géométriques de l'acquisition d'images (position de l'axe optique par rapport à l'image, valeur de la distance focale, distorsion, etc.). Pour les cas où ces paramètres sont inconnus, la modélisation doit se passer de certains éléments indispensables à la reconstruction géométrique complète. Néanmoins, si l'on admet de travailler en géométrie projective, qui est parfaitement adaptée à cette situation, on peut quand même obtenir des éléments très utiles, et cette situation est fréquemment rencontrée en vision par ordinateur. On utilise alors encore une forme quadratique, mais cette fois basée sur la "matrice fondamentale" (autre terme consacré).

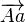
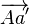
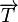
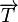
L'identification des points homologues a longtemps exigé une intervention humaine, et représentait alors une phase de travail assez coûteuse. Désormais, on parvient de façon de plus en plus efficace à l'obtenir de façon automatique, les algorithmes les plus employés étant celui de Harris (détection des éléments d'images qui s'apparentent à des coins) et plus récemment celui de Lowe (méthode appelée SIFT, pour Scale Invariant Feature Transform).