Isopérimétrie - Définition

Introduction

La forme d'une bulle de savon est une réponse à une question d'isopérimétrie. Sa géométrie est sphérique car c'est le solide qui englobe le plus vaste volume dans une surface de mesure donnée.

En géométrie plane, l'isopérimétrie traite, en particulier, la question de trouver la surface la plus vaste possible, pour un périmètre donné. La réponse est intuitive, c'est le disque. Ce problème, d'apparence anodin, fait appel à des théories sophistiquées pour obtenir une démonstration rigoureuse. À cet égard, il ressemble un peu au théorème de Jordan, indiquant qu'une boucle la plus simple possible (sans croisement) divise un plan en deux parties, l'intérieur de la boucle qui est borné, et l'extérieur qui ne l'est pas. En conséquence, on simplifie parfois le problème isopérimétrique en limitant les surfaces autorisées. Par exemple, on cherche le quadrilatère ou le triangle d'aire la plus vaste possible, toujours pour un périmètre donné. Les solutions respectives sont le carré et le triangle équilatéral. De manière générale, le polygone à n sommets ayant la plus grande surface, à périmètre donné, est celui qui se rapproche le plus du cercle : c'est le polygone régulier.

L'isopérimétrie ne se limite pas à ces questions. On recherche aussi une zone d'aire la plus vaste possible pour un périmètre donné, avec des géométries différentes. Par exemple, dans le cas d'un demi-plan, la réponse est le demi-disque. La question du solide de plus grand volume, enveloppé dans une surface de mesure fixée est naturellement dans le domaine de l'isopérimétrie. La bulle de savon, qui cherche à envelopper un volume d'air donné dans la surface la plus petite possible, indique la solution : une sphère.

Ce concept donne naissance à une famille de théorèmes, dit isopérimétriques, à des majorations dites inégalités isopérimétriques, ainsi qu'à un rapport, appelé quotient isopérimétrique. En dimension 2, l'inégalité isopérimétrique indique qu'une surface de périmètre p et d'aire a vérifie la majoration suivante :

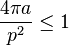
Le terme de gauche, est appelé quotient isopérimétrique, il est égal à 1 si, et seulement si la surface est un disque.

Si l'origine de cette question date d'au moins 2 900 ans, ce n'est qu'en 1895, à l'aide de méthodes dérivées du théorème de Minkowski que la question est définitivement résolue sous sa forme antique. Ces méthodes permettent de démontrer le théorème isopérimétrique et de le généraliser à des dimensions supérieures dans le cas d'une géométrie euclidienne.

Cet article traite uniquement des aspects élémentaires de cette question. Des éléments de réponse, faisant usage d'outils mathématiques plus sophistiqués, sont proposés dans l'article Théorème isopérimétrique.

Fragments d'histoire

Didon applique le théorème isopérimétrique pour l'achat du terrain à l'origine de la fondation de Carthage.

La légende raconte que la ville de Carthage, fut fondée 814 av. J.-C. par la princesse phénicienne Elissa, surnommée Didon. Elle demanda au roi de Numidie Iarbas l'octroi d'un terrain pour s'y installer. Iarbas, réticent, lui accorda le droit de choisir un lopin de terre que pourrait contenir la peau d'un bœuf. La rusée Didon découpa en une fine lamelle la peau, qui devint une longue lanière de 4 km de long. Elle fit étendre cette lanière sur un demi-cercle dont les deux extrémités touchaient la côte, rectiligne à l'endroit où elle se trouvait. La reine avait intuitivement trouvé la solution au problème isopérimétrique dans un demi-plan euclidien. Ce problème est résolu lorsqu'est trouvée la surface la plus grande possible, pour un périmètre donné. Le demi-cercle est en effet la courbe que doit suivre la lanière pour délimiter la plus grande surface possible, dans ce cas particulier.

La méthode, consistant à mesurer une surface à l'aide de son périmètre, est fréquente durant l'antiquité grecque. Homère indique que la ville de Troie fait 10 200 pas, indiquant par là qu'en faire le tour demande une marche de 10 200 pas. La solution du problème isopérimétrique dans le plan euclidien est connue par certains depuis le V^e siècle av. J.-C., au moins pour le cas du polygone à n côtés. Il porte le nom de théorème isopérimétrique. À l'époque des grecs, tous ne semblent pas au courant de ce résultat et de ses conséquences. Proclos mentionne le cas de tricherie de géomètres datant de cette époque. Des terrains étaient divisés en différents lopins de même périmètre mais de surfaces différentes, les géomètres, responsables du partage, obtenaient les plus grosses parcelles. La supercherie fut découverte au moment des moissons, dont l'abondance est proportionnelle à la surface et non au périmètre.

Théon d'Alexandrie et Pappus attribue à Zénodore les premières démonstrations. Il prouve que parmi tous les polygones à n côtés et même périmètre, seul celui régulier est candidat à être la réponse au problème isopérimétrique. Il découvre aussi que le disque d'un périmètre donné possède une surface supérieure à celle de n'importe quel polygone régulier. Il aurait aussi démontré que la sphère est le solide ayant un plus grand volume que tout polyèdre de même surface.

Les mathématiques grecs n'ont pas les moyens d'aller au-delà. Leurs démonstrations restent partielles, même si leurs auteurs n'ont pas conscience de l'aspect incomplet des preuves. Ils ne disposent pas non plus des outils mathématiques qui auraient permis d'aller plus loin. Les mathématiciens arabes s'approprient le savoir des grecs sur cette question. Abū Ja'far al-Khāzin écrit un traité résumant tout le savoir de son époque sur l'isopérimétrie. Ils développent les moyens d'aller plus loin. Nasir ad-Din at-Tusi un mathématicien du XIII^e siècle développe, dans son traité du quadrilatère, suffisamment la trigonométrie pour présenter des preuves complètes dans le cas des triangles ou des rectangles.

Il faut ensuite attendre les mathématiques européennes du XIX^e siècle pour d'autres progrès. En 1836, Jakob Steiner obtient un premier résultat nouveau. Sous réserve d'admettre l'existence d'une solution en dimension 2, alors cette solution est nécessairement le disque. Pour une preuve complète en dimension 2, il faut attendre les travaux de Karl Weierstrass et Hermann Minkowski, elle devient rigoureuse vers 1895. Cette partie de l'histoire est traitée dans l'article théorème isopérimétrique.