Polynôme formel - Définition
La liste des auteurs de cet article est disponible ici.
Factorisation
Équation algébrique
La question à l'origine de la découverte du polynôme est celle de l'équation. Pendant près de 1.000 ans, cette question et les méthodes pour y parvenir représentaient l'essentiel de l'algèbre. Si P est un polynôme à coefficients dans le corps K, noté :

La question revient à trouver les valeurs xi, appelées racines, telles que l'expression suivante soit nulle :
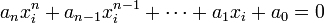
Bien avant la formalisation moderne de la notion de fonction, on avait remarqué que remplacer l'indéterminée par une valeur donne le même résultat dans toutes les expressions de P. Si k est un élément de K, souvent un nombre, il est possible de diviser P par le polynôme X - k. Le reste est un polynôme constant c, car de degré strictement inférieur à celui de X - k. On obtient une nouvelle expression de P, à savoir P = Q.(X - k) + c.
Substituer la valeur k à l'indéterminée X donne le même résultat dans l'expression de droite et de gauche. Si c est non nul, k n'est pas racine car l'expression est égale à c. En revanche si c est nul, alors k est racine.
Racine et factorisation d'un polynôme — Soit P un polynôme à coefficients dans le corps K, un nombre r est racine du polynôme P si, et seulement si le polynôme X - r divise le polynôme P
Vue sous l'angle arithmétique, la recherche des racines d'un polynôme est équivalente à la recherche des facteurs du premier degré de P. Ces facteurs sont nécessairement irréductibles, le produit de deux polynômes non constants n'est en effet jamais de degré 1, car le produit de deux polynômes est de degré la somme des degrés des deux polynômes. Résoudre une équation revient à trouver les facteurs irréductibles d'un type particulier, ceux du premier degré. On retrouve un problème déjà connu en arithmétique.
L'intégralité des méthodes de résolutions algébriques d'une équation peuvent être vues comme une factorisation du polynôme en éléments irréductibles du premier degré. La méthode classique de l'équation du second degré se résume finalement à cela. On peut en déduire un premier résultat.
Proposition — Un polynôme à coefficients dans K n'admet jamais plus de racines que son degré.
Si le polynôme P ne comporte, dans sa décomposition en facteurs irréductibles, que des polynômes du premier degré, alors une analyse sur le terme du plus haut degré indique que P contient autant de facteurs que son degré, noté ici n. Ainsi un polynôme P ne peut contenir plus de facteurs du premier degré que son degré. Dans le cas général, P est le produit d'un polynôme qui n'est pas divisible par un polynôme du premier degré et de m facteurs du premier degré avec m plus petit que n, ce que l'on peut écrire :
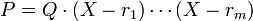
Le polynôme Q est irréductible, ainsi si l'on remplace dans son expression l'indéterminée par une valeur k quelconque, on ne trouve jamais 0, sinon X - k diviserait Q. Comme le produit de nombres non nuls n'est jamais nul, pour que le produit de droite soit nul quand on remplace l'indéterminée par une valeur k, il faut qu'un des facteurs soit nul c'est-à-dire égal à l'un des rj, ce qui démontre la proposition.
Polynômes irréductibles à coefficients dans C, R et Q
Selon le choix du corps des coefficients, les polynômes irréductibles n'ont pas la même forme. Considérons le polynôme P égal à X5 - X4 - 4X + 4. Rechercher ses facteurs irréductibles du premier degré revient à résoudre l'équation polynomiale associée. Si cette équation est étudiée dans C, le théorème fondamental de l'algèbre indique l'existence d'au moins une racine. Dans le cas particulier étudié on trouve la racine évidente 1, et une division euclidienne montre que :
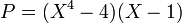
Le polynôme P s'écrit comme le produit de deux polynômes dont un du premier degré. L'usage du même théorème montre que l'autre polynôme possède au moins une racine, ce qui indique l'existence d'un autre facteur du premier degré. De proche en proche on factorise P en polynômes du premier degré. En pratique une identité remarquable appliqué 3 fois permet la factorisation de l'exemple étudié :
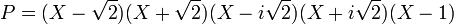
Et dans le cas général :
Polynôme irréductible dans C — Les seuls polynômes à coefficients dans le corps des nombres complexes irréductibles, sont ceux du premier degré.
La même équation sur R donne des résultats différents. Le terme i, désignant l'unité imaginaire, n'existe pas. La factorisation donne :
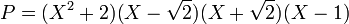
Il est aisé de se rendre compte que le premier facteur est irréductible. Remplacer l'indéterminée par une valeur donne toujours un nombre plus grand que 2, le polynôme X2 + 2 ne contient aucun diviseur du premier degré et, comme il est de degré 2, il est nécessairement irréductible. Dans le cas général :
Polynôme irréductible dans R — Les seuls polynômes irréductibles à coefficients réels, sont ceux du premier degré et ceux du deuxième degré ayant un discriminant strictement négatif.
Dans Q, l'exemple choisi montre qu'il n'existe qu'un seul facteur du premier degré, car la racine de 2 n'est pas un nombre rationnel. Les polynômes irréductibles à coefficients dans Q sont beaucoup plus variés, on en trouve de tous les degrés, comme le montre le critère d'Eisenstein.
-
- Un polynôme irréductible et à coefficients dans R est de degré 1 ou 2 :
Considérons un polynôme P à coefficients dans R de degré strictement supérieur à 2, on va montrer qu'il n'est pas irréductible. On le note :
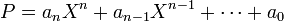
Le théorème fondamental de l'algèbre indique que ce polynôme admet au moins une racine r, s'il est considéré comme un polynôme à coefficients dans C. Si cette racine est réelle, le polynôme X - r divise P, et P n'est pas irréductible. Sinon, cette racine vérifie l'égalité, dans C :
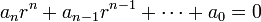
Le conjugué de tout élément de R, considéré comme un élément de C est égal à lui-même. En appliquant l'application conjuguée à la dernière égalité, on obtient :
On en déduit que le conjugué de r, nécessairement différent de r car r n'est pas réel, est aussi une racine de P, considéré comme un polynôme complexe. On en déduit que les deux polynômes unitaires du premier degré et de racines r et son conjugué, divise P. Leur produit Q, égal à X2 + |r|2 divise aussi P dans C. La division euclidienne de P par Q dans l'anneau des polynômes à coefficients dans R peut aussi être vue comme la division euclidienne de P par Q dans C[X]. Comme le résultat d'une division euclidienne est unique, ces deux divisions sont les mêmes dans R[X] et dans C[X]. Comme le reste est nulle dans C[X], il est aussi nul dans R[X] et Q divise P dans R. Ce qui montre que P n'est pas irréductible et termine la démonstration.
Coefficients et racines
À condition d'accepter d'élargir l'ensemble de nombres, pour les configurations classiques comme les nombres rationnels, réels ou complexes, il est toujours possible de factoriser un polynôme P. Cela donne deux manières d'écrire P. En utilisant les mêmes notations que précédemment :
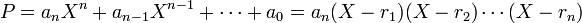
Ici r k pour k variant de 1 à n, désigne les différentes racines du polynôme P. Les valeurs que prennent les r k peuvent être semblables, on parle alors de racines multiples. La décomposition correspond à celles des facteurs premiers de P, la constante an supposée non nulle, correspond à l'élément du groupe des unités, sa valeur est celle du coefficient du monôme dominant.
Dans le cas du polynôme unitaire du deuxième degré, l'égalité devient :
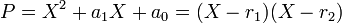
Le développement du terme de droite donne les relations :
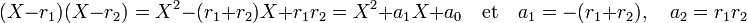
Cette factorisation donne une relation entre les coefficients et les racines. Elle se généralise.
Si l'on remplace maintenant r1 et r2 par deux indéterminées X et Y, on obtient deux polynômes X.Y et X+Y dit symétriques. Un polynôme à plusieurs indéterminées est dit symétrique si une permutation des indéterminées ne modifie pas le polynôme. Ainsi X.Y est symétrique, mais X2 + Y ne n'est pas. Pour générer des polynômes symétriques à n variables, il suffit d'utiliser ce procédé avec un polynôme de degré n. On obtient exactement n polynômes symétriques. Tous les polynômes symétriques s'obtiennent par combinaison linéaires de produits de ces n polynômes symétriques.

















































