Polynôme formel - Définition

Dérivée formelle

Définition

Il existe une application linéaire de A[X] parfois très utile, elle est appelée dérivée formelle. Comme toute application linéaire, elle est parfaitement définie par la connaissance de l'image d'une base.

On peut être surpris par une telle définition, l'élément n qui multiplie le monôme est un entier, rien ne dit que A contient l'ensemble des entiers. Le terme n indique en fait, soit l'élément 1 + 1 +...+ 1 itéré n fois, soit si l'anneau A ne contient pas d'élément neutre pour la multiplication n.X^n-1 désigne le terme X^n-1 additionné n fois avec lui-même.

Si A est l'anneau des entiers ou le corps des nombres complexes, la dérivée formelle est le pendant de l'application dérivée dans le monde des polynômes formels. La définition présentée ici s'applique néanmoins à n'importe quel anneau de polynôme construit sur un anneau commutatif.

Si le polynôme P s'écrit de la manière habituelle, on a l'expression P' de sa dérivée formelle :

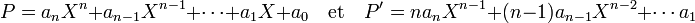
Propriétés

On dispose de certaines propriétés élémentaires de la dérivée, le noyau de l'application linéaire est composée des polynômes constants, le degré de la dérivée d'un polynôme formel de degré n est égal à n - 1, en conséquence, l'application n + 1 fois de la dérivée sur un polynôme de degré n est nulle. Enfin, si P et Q sont deux polynômes :

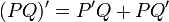
Une autre propriété relie l'existence de racines multiples à la dérivée formelle, on dit qu'un polynôme à coefficient dans K est séparable si et seulement s'il admet autant de racines distinctes que son degré, dans au moins un corps L contenant K.

Le polynôme à coefficients dans Q, l'ensemble des nombres rationnels : X² + 2 est séparable, car il admet deux racines distinctes dans C le corps des nombres complexes, qui contient Q. Il est bien premier avec sa dérivée formelle, égal à 2X. On trouve la démonstration dans l'article Extension séparable.

Développement de Taylor

Dans l'univers des applications continues définies pour tout nombre réel et à valeurs réelles, deux fonctions ayant même dérivée ne diffèrent que par une constante. Ce résultat est une conséquence du théorème fondamental de l'analyse. Ce résultat ne se généralise pas toujours dans le monde des polynômes formels. Supposons que sur l'anneau A, l'itéré de l'addition de 1_A n fois soit égal à 0_A, on parle alors d'anneau de caractéristique n. Les dérivées des polynômes X_n + X et X sont égales : celui constant égal à 1. Pourtant ces deux polynômes ne diffèrent pas d'une constante. Cette situation ne se produit pas si l'anneau est de caractéristique 0, c'est-à-dire si quel que soit n, entier strictement positif le n^ième itéré de l'unité 1_A n'est pas nul.

Dans ce cas, le développement de Taylor s'applique encore sur les polynômes formels.

Développement de Taylor — Soit A un anneau commutatif unitaire, intègre et de caractéristique 0, soit P un polynôme de A[X] de degré n et a un élément de A. La formule suivante, dite développement de Taylor, est vérifiée :

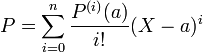
Cette formule mérite quelques explications, le terme P⁽ⁱ⁾(a) désigne l'élément de A obtenu en substituant a à l'indéterminée X. L'élément i ! désigne un itérée pour l'addition de l'unité de l'anneau, c'est exactement l'itéré de l'unité additionné avec elle-même factorielle i fois. La division n'est pas toujours définie sur A, en revanche le terme P⁽ⁱ⁾(a) est toujours un multiple de i !, et il existe un unique élément b_i de A tel que b_i.i ! soit égal à P⁽ⁱ⁾(a), ce qui permet de donner un sens au développement de Taylor.

Supposons, dans un premier temps que a soit égal à 0. Une simple récurrence montre que la constante du polynôme dérivée i ^ième est égal à a_i.i !. La dérivée i ^ième au point 0 est un multiple de i !. comme l'anneau A est intègre, il existe un unique élément de A tel que le produit de cet élément avec i ! soit égal à la dérivée i ^ième au point 0. On en déduit le résultat suivant, parfois appelé développement de Taylor-Young :

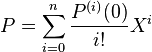
Soit Q le polynôme égal à P(X + a), la formule précédente devient :

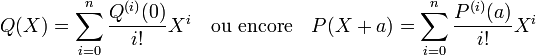
En remplaçant X + a par X, on obtient la formule annoncée.

 

Résultant, discriminant

Le résultant de deux polynômes est le déterminant d'une matrice construite à l'aide des deux polynômes. Ce déterminant est nul si, et seulement si, les deux polynômes sont premiers entre eux. Le discriminant d'un polynôme P est, à un facteur multiplicatif près, le résultant du polynôme et de sa dérivée, ce qui permet d'écrire que :

Si a est le coefficient du monôme dominant, n le degré du polynôme et α _k, pour k variant de 1 à n, les racines du polynôme P, son discriminant Δ(P) est égal à :

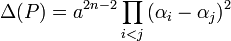
Le discriminant s'exprime aussi en fonction des coefficients du polynôme, l'expression est néanmoins complexe si n est élevé. Dans le cas de la dimension 2 et si le polynôme P s'écrit aX² + bX + c, on retrouve l'expression classique :

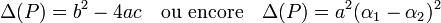
Ce qui permet de retrouver aisément les formules donnant les racines de l'équation en fonction des coefficients, sachant que l'opposé de la somme des racines est égal à b. Si n est strictement plus grand que 2, le discriminant n'offre pas de moyen simple d'exprimer les racines.