Polynôme formel - Définition
La liste des auteurs de cet article est disponible ici.
Anneau des polynômes
Écriture d'un polynôme
Pour construire rigoureusement l'anneau des polynômes A[X], il faut définir « le polynôme X appelé indéterminée », cette partie est traité dans l'article détaillé. Pour écrire un polynôme sous sa forme générale, il faut disposer d'un nombre fini d'éléments de A, par exemple a0, a1, a2,... ,ak,..., an, tel que an est différent de 0. On peut écrire le polynôme P sous les deux formes suivantes :
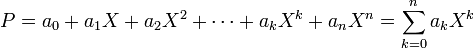
Égalité de deux polynômes — Deux polynômes sont égaux si, et seulement si, la suite de leurs coefficients sont égaux. En particulier un polynôme est nul si, et seulement si, la suite de ses coefficients est nulle.
Un monôme est un terme de la forme a.Xp, constitutif du polynôme, a est appelé le coefficient du monôme et p son degré. Le plus grand degré des monômes à coefficients non nuls, ici n, est appelé le degré du polynôme, sauf si le polynôme est nul, on dit alors que son degré est moins l'infini. Le plus petit degré des monômes à coefficient non nuls est appelé la valuation du polynôme, sauf si le polynôme est nul, on dit alors que sa valuation est plus l'infini.
Opération sur les polynômes
L'ensemble des polynômes A[X] ressemble à bien des égards à celui des entiers. Les deux ensembles sont équipés de deux opérations : l'addition et la multiplication et ces opérations vérifient des propriétés regroupées sous le nom d'axiomes et définissant une structure dite d'anneau. L'élément neutre de l'addition est le polynôme constant 0 et si A contient un élément neutre pour la multiplication, généralement noté 1, l'élément neutre de A[X] pour la multiplication est le polynôme constant 1. L'expression polynôme constant signifie qu'il s'exprime uniquement à l'aide d'une constante et sans monôme de degré strictement supérieur à 0.
L'analogie va plus loin M. Delord remarque que l'écriture décimale positionnelle du nombre 3021 s'écrit aussi 3.103 + 2.101 + 1. Cette écriture possède des analogies avec le polynôme 3X3 + 2X + 1. La valeur 10 a été remplacée par l'indéterminée. Cette analogie est flagrante si l'on cherche à additionner 3021 avec 21. Les coefficients des différentes puissances de 10 s'additionnent entre eux comme les coefficients des puissances de l'indéterminée. Dans un cas on trouve 3.103 + 4.101 + 2 et dans l'autre 3X3 + 4X + 2. Une multiplication des deux nombres et des deux polynômes donnent encore des résultats semblables :
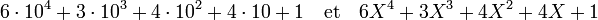
L'analogie n'est pas totale, sa limite apparaît si une retenue se présente dans les opérations. Les mécanismes de retenues dans l'addition et la multiplication des entiers en système décimal ne sont pas les mêmes que pour les polynômes.
La somme de deux monômes de même degré est un monôme de même degré et de coefficients la somme de deux coefficients :
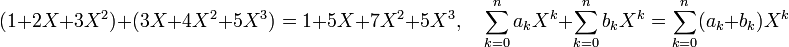
La multiplication est un peu plus difficile, elle s'appuie sur la règle, si n et m sont deux entiers positifs : Xn.Xm = Xn+m. On peut prendre un exemple, issu d'une identité remarquable :
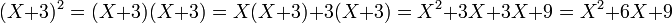
Dans le cas général, on obtient :
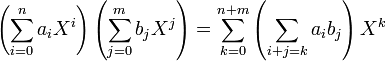
Le degré du produit de deux polynômes est la somme des degrés des deux polynômes. C'est pour que cette règle soit toujours vérifiée que le degré du polynôme nul est défini comme égal à moins l'infini. Ces propriétés sont explicitées et démontrées dans l'article détaillé.
Division euclidienne
Si tous les éléments non nuls de l'anneau A sont inversibles comme pour Q, R ou C , on dit que A est un corps, noté ici K. L'ensemble des polynômes à coefficients dans K est alors équipé d'une division :
Division euclidienne — Soit A et B deux polynômes à coefficients dans un corps K. Si B est non nul, il existe un unique couple de polynômes (Q, R) à coefficients dans K tel que A soit égal à B.Q + R et que le degré de R soit strictement plus petit que celui de B.
Une autre division, appelée division selon les puissances croissantes, existe. Elle est développée dans l'article détaillé.
Arithmétique
La division euclidienne est à l'origine des résultats de l'arithmétique élémentaire sur les entiers. Elle permet de démontrer l'identité de Bézout, qui indique que si a et b n'ont pas de diviseurs communs autres que 1 et -1, il existe deux entiers p et q tel que ap + bq = 1. La division euclidienne sur les polynômes à coefficients dans un corps commutatif montre l'équivalent :
Identité de Bézout pour les polynômes — Deux polynômes P et Q à coefficients dans un corps K sont premiers entre eux si, et seulement si, il existe deux polynômes A et B tels que :
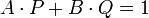
Deux polynômes sont dit premiers entre eux lorsque les seuls diviseurs communs sont les polynômes constants non nuls. L'identité de Bézout permet de montrer le lemme d'Euclide, qui indique que si P est un polynôme irréductible qui divise un produit de polynômes A.B, il divise soit A, soit B. Enfin, dans l'univers des polynômes, l'équivalent des nombres premiers sont les polynômes irréductibles et unitaire, ce qui permet d'exprimer un équivalent du théorème fondamental de l'arithmétique :
Décomposition en facteurs premiers — Un polynôme non nul, à coefficients dans K, se décompose de manière unique en un produit, composé d'un polynôme constant et d'un produit de polynômes unitaires irréductibles.
Les résultats sur les plus petits communs multiples et les plus grands communs diviseurs s'appliquent exactement comme pour les entiers.
S'il existe des coefficients non nuls et non inversibles, l'arithmétique est un peu différente, elle est traitée dans l'article détaillé.

















































