Programme d'Erlangen - Définition

Introduction

Le programme d'Erlangen est un programme de recherche publié par le mathématicien allemand Felix Klein en 1872, dans le mémoire Vergleichende Betrachtungen über neuere geometrische Forschungen (ou « Étude comparée de différentes recherches récentes en géométrie »). L'objectif est de comparer les différentes géométries apparues au cours du XIX^e siècle pour en dégager les points de similitude : on peut ainsi plus clairement distinguer la géométrie affine, la géométrie projective, la géométrie euclidienne, la géométrie non euclidienne au travers d'une vision globale. La clef de voûte de ce programme est de fonder la géométrie sur les notions d'action de groupe et d'invariant. Ce programme apparut comme une remise en question de la géométrie et influa très fortement sur son développement et son évolution. Encore aujourd'hui sa philosophie influence de nombreux mathématiciens, ainsi que des programmes d'enseignement et de recherche.

La lecture de cet article demande une certaine familiarité avec les concepts et le vocabulaire des actions de groupes.

Contexte historique et principes

Depuis l'écriture des Éléments d'Euclide (et même avant), la géométrie se limitait à l'étude de l'espace environnant, c'est-à-dire à la géométrie euclidienne en dimensions 2 ou 3. Le XIX^e siècle a connu un épanouissement des mathématiques et en particulier de la géométrie. En réponse à la question de l'indépendance des axiomes d'Euclide, de nouvelles géométries furent introduites, à l'instar de la géométrie hyperbolique ou de la géométrie projective. À l'époque, on voyait ces géométries non pas comme des espaces de travail donnés mais plutôt comme des modèles répondant à une collection d'axiomes desquels les résultats géométriques devaient se déduire. Cette vision de la géométrie, dite géométrie synthétique, se place dans une volonté de rigueur mathématique.

Felix Klein.

En prenant possession de sa chaire à l'université d'Erlangen, alors âgé de vingt-quatre ans, Klein devait selon la tradition proposer un programme de travail. Le sien est une remise en question de cette vision traditionnelle. Son idée est d'appuyer la géométrie sur la théorie des groupes, et de placer le concept de symétrie (ou transformation) au centre de la géométrie.

La notion de groupe avait été introduite par Évariste Galois en 1831 pour étudier le problème de la résolubilité des équations polynomiales. C'est cette même notion que Klein emploie pour comprendre la géométrie, mais dans un tout autre contexte. Dans le programme d'Erlangen, une géométrie est décrite comme l'action d'un groupe G sur un ensemble X. Il s'agit moins d'une définition que d'une recherche d'esthétique. Dans ce contexte, on définit un objet géométrique par le lieu des points de X invariants par un sous-groupe isotropique de G. On peut aussi s'intéresser à une classe d'objets laissée invariante par l'action induite de G, qui forme alors un nouvel espace sur lequel opère G, et on cherche alors classifier ces objets pour l'opération du groupe G. On peut aussi prendre un sous-groupe de G et comparer les deux géométries obtenues.

Voici des exemples qui permettent d'illustrer ces principes tout en restant dans le cadre de la géométrie plane. On considère un plan euclidien X et trois groupes : le groupe affine de X, le groupe des isométries de X et le groupe des similitudes affines de X. Ces groupes opèrent transitivement sur X et définissent trois géométries.

• Dans un premier exemple, on s'intéresse aux couples de points distincts de X (ou aux segments de X). Le groupe affine et le groupe des similitudes opèrent transitivement sur l'ensemble de ces couples, et il n'y alors pas lieu de les classifier pour ces groupes. Pour le groupe des isométries, ce qui permet de les classifier c'est la distance mutuelle des points du couple.

• Dans un deuxième exemple, on s'intéresse aux triangles de X. Le groupe affine opère transitivement sur l'ensemble des triangles, et il n'y alors pas lieu de les classifier. Pour le groupe des similitudes affines, ce qui permet de classifier les triangles, ce sont les angles des triangles (cas de similitudes des triangles). Pour le groupe des isométries, ce qui permet de classifier les triangles, ce sont les longueurs des côtés (cas d'égalité des triangles).

• Le groupe affine de X opère transitivement sur l'ensemble des couples de droites sécantes. Pour le groupe des isométries (ou des similitudes affines), on peut opérer une classification à l'aide de l'angle de droites (c'est un nombre réel).

L'on peut aussi considérer les couples de droites parallèles de X, et alors le groupe affine et le groupe des similitudes affines opèrent transitivement sur cet ensemble et la distances entre les droites sert à les classifier pour le groupe des isométries. Du point de vue de la géométrie projective, si on prend le complété projectif P de X (c'est un plan projectif), alors les droites de X deviennent des droites de P, et alors les deux types de couples de droites de X se confondent dans X pour le groupe projectif de P, et ce groupe opère transivement sur les couples de droites distinctes de P (deux droites de P sont nécessairement sécantes et il n'y donc pas de droites parallèles distinctes dans P).

• Les coniques propres de X se répartissent en trois orbites pour le groupe affine : les ellipses (cercles compris), les hyperboles et les paraboles. Pour le groupe des similitudes affines de X, ces coniques propres de X forment une classe d'objets invariants, classifiées par leur excentricité. Pour le groupe des isométries de X, l'« équation normalisée » permet la classification.

Du point de vue de la géométrie projective, si on prend le complété projectif P de X (c'est un plan projectif), alors le groupe projectif de P opère transitivement sur les coniques propres de P, alors que les traces sur X de ces coniques de P sont exactement les coniques propres de X : ainsi, en ajoutant une droite à l'infini de X, on ne peut plus distinguer les coniques de X.

En pratique, les groupes qui interviennent dans les géométries du XIX^e siècle sont les groupes classiques, c'est-à-dire des sous-groupes des groupes linéaires , et de sous-groupes des groupes affines et des groupes projectifs qui leurs sont associés. Ces groupes sont encore très utilisés en géométrie.

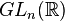
Le second mérite du programme d'Erlangen est de clarifier les particularités de chaque type de géométrie. Par exemple, la géométrie projective rend bien compte de l'alignement des sections coniques, mais non des cercles, des angles et des distances, car ces notions ne sont pas invariantes par les transformations projectives (il suffit de les imaginer en perspective pour le comprendre). Dans l'optique de ce programme, comprendre la liaison entre les différents types de géométrie revient alors à considérer des sous-groupes d'un groupe de symétries.

Selon Bourbaki, la géométrie classique serait morte en tant que champ de recherche, puisque, avec la clarté obtenue en classifiant les résultats des géométries d'un espace à l'aide des groupes dont il relève, et surtout depuis les progrès de la théorie des invariants, on peut obtenir de manière presque automatique et systématique les résultats de la géométrie classique. Il reste toutefois à trouver dans quel langage ces résultats seront les plus simples et élégants : « Dépassée en tant que science autonome et vivante, la géométrie classique s'est ainsi transfigurée en un langage universel de la mathématique contemporaine, d'une souplesse et d'une commodité incomparables. » (N. Bourbaki, Éléments de mathématiques, Algèbre, chap. 9, Notes historiques (1959).)