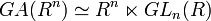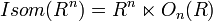Programme d'Erlangen - Définition

Influence sur la géométrie moderne

L'impact du programme d'Erlangen dépasse complètement la vision de Felix Klein. Elle se retrouve dissimulée à travers chaque utilisation des groupes en géométrie. Évidemment, le programme d'Erlangen n'aurait pu correspondre avec les nouvelles structures géométriques rencontrées au cours du XX^e siècle : variété différentielle, variété algébrique, ... Mais une trace demeure présente.

• En géométrie différentielle, un espace homogène est une variété différentielle X sur laquelle agit transitivement un groupe de Lie. Les espaces homogènes jouent un rôle central, et plus particulièrement en géométrie riemannienne. La classification des espaces symétriques s'appuie sur la géométrie des espaces homogènes (parmi les espaces symétriques, on retrouve les espaces euclidiens, les sphères euclidiennes, les espaces elliptiques et les espaces hyperboliques).

• Le groupe fondamental d'un espace topologique X agit sur tout revêtement Y de X. Cette action est centrale dans la théorie des revêtements. Elle permet par exemple la classification des revêtements à isomorphisme près.

• Une variété différentielle est un espace topologique obtenu par recollement d'ouverts de Rⁿ par des difféomorphismes, ce qui permet d'y faire du calcul différentiel. Mais on peut vouloir restreindre la donnée des recollements. En recollant des ouverts de Rⁿ par des isométries affines (resp. applications symplectiques affines, resp. applications affines), on obtient exactement les variétés riemanniennes plates (resp. les variétés symplectiques, resp. les variétés munies d'une connexion de courbure nulle). En restreignant les groupes, on enrichit la structure géométrique. On obtient la théorie des pseudogroupes de transformations.

• En considérant sur les espaces tangents d'une variété différentielle X de dimension n toutes les bases, on obtient un espace ce que l'on appelle le fibré des repères de X, et le groupe linéaire réel de degré n opère sur ce nouvel espace. En enrichisant la variété X d'une structure vérifiant certaines propriétés (les G-structures, une métrique riemannienne par exemple), on considère les repères adaptés à cette structure (les repères orthonormaux, par exemple) et alors le sous-groupe du groupe linéaire correspondant (le groupe orthogonal, dans cet exemple) opère sur ce nouvel espace de repères, de manière non transitive en général. Réciproquement, si on considère un sous-groupe de Lie du groupe linéaire (le groupe orthogonal par exemple), on peut déterminer les structure sur la variété qui admette ce groupe comme groupe structural (toutes les métriques riemanniennes dans cet exemple). C'est Élie Cartan qui a introduit ces concepts, et, avec la théorie des connexions, il a pu réconcilier le programme d'Erlangen avec la géométrie riemannienne de Bernhard Riemann.

Les différentes géométries à la lumière du programme d'Erlangen

Ce tableau donne la correspondance entre les principales géométries introduites au XIX^e siècle et les actions de groupes :

Géométrie	Espace	Groupe	Invariants
Affine	Espace affine Rn	groupe des isomorphismes affines de Rn	Sous-espaces affines
Euclidienne	Espace euclidien Rn,g	groupe des isométries affines de Rn	Sous-espaces affines, sphères
Sphérique	Sphère euclidienne Sn	On + 1(R): groupe orthogonal	Grands cercles
Projective	Espaces projectifs réels PnR	PGnR : groupe projectif	Sous-espace projectif
Elliptique	Espace projectif réel PnR	POn + 1(R) = On + 1(R) / Z / 2Z: groupe projectif orthogonal	Sous-espaces projectifs

Une des idées fondamentales de Klein consiste à plonger les différentes géométries dans la géométrie projective : on fixe une figure d'un espace projectif et on dérive de cette figure, ou d'une figure qui lui est associée, le groupe des transformations projectives qui la laisse stable. On cherche alors des invariants et des quantités qui permettent de les classifier sous l'action du groupe. On obtient de cette façon les principales géométries classiques : la géométrie affine, la géométrie euclidienne, la géométrie sphérique la géométrie elliptique, la géométrie hyperbolique et la géométrie conforme. Puisque la géométrie projective peut être basée sur l'algèbre linéaire, toutes ces géométries admettent des modèles basés sur l'algèbre linéaire. De plus, l'algèbre linéaire est un outil théorique puissant pour l'étude de ces géométries.

On interprète ici les principales géométries comme sous-géométries de la géométrie projective (ou affine).

• La géométrie affine peut obtenue à l'aide de la géométrie projective de la manière suivante : on prend un espace projectif P déduit d'un espace vectoriel réel E de dimension finie (P_nR par exemple) et on fixe un hyperplan L de P (P_{n − 1}R par exemple) et on prend le stabilisateur G de L pour le groupe projectif de P (qui induit par le groupe linéaire de E). Ensuite, le complémentaire de L dans P s'identifie à un espace affine réel de dimension n (Rⁿ dans l'exemple) et le groupe de transformations induites sur ce espace affine est son groupe affine (le groupe affine de Rⁿ dans l'exemple). En fait, on a fait l'opération inverse de la complétion projective d'un espace affine, qui consiste à plonger un espace affine dans un espace projectif et de plonger son groupe affine dans le groupe projectif. Ainsi, la géométrie affine est un sous-géométrie de la géométrie projective. Tout ceci fonctionne si on remplace le corps des nombres réels par le corps des nombres complexes (ou par un corps commutatif).

• On peut interpréter la géométrie euclidienne avec son groupe des similitudes en termes de géométrie projectif (c'est plus abstrait). Il y a sur P_{n − 1}R ce que l'on appelle une « quadrique imaginaire » : la norme au carrée de Rⁿ définie un polynôme homogène réelle de degré 2 de Rⁿ et, en remplaçant les coordonnées réelles par des coordonnées complexes, on obtient un polynôme homogène complexe de degré 2 de Cⁿ (même équation, mais en variables complexes). Les points de l'espaces projectif complexe P_{n − 1}C qui annulent ce polynôme est une quadrique projective de P_{n − 1}C (une conique projective si n = 2 et deux points si n = 2). C'est la quadrique imaginaire de P_{n − 1}R. On a vu dans l'exemple précédent de la géométrie affine, que le groupe affine de Rⁿ s'identifie à un sous-groupe du groupe projectif de P_nR. Le groupe des similitudes affines de Rⁿ est le sous-groupe du groupe projectif (ou du groupe affine) des transformations qui laissent stable la quadrique imaginaire (on remplace les coordonnées réelles par des coordonnées complexes, et tout ici a un sens). Ainsi la géométrie euclidienne semblable est une sous-géométrie de la géométrie projective.

• On peut donner une autre interprétation de la géométrie elliptique. Pour cela, on reprend la quadrique imaginaire de P_nR de l'exemple précédent (on augmente la dimension de 1). Alors le groupe projectif orthogonal de P_nR est le sous-groupe du groupe projectif de P_nR qui laisse stable la quadrique imaginaire. On dit que cette quadrique imaginaire est l'absolu de l'espace elliptique P_nR. En peut ainsi dire que l'hyperplan à l'infini d'un espace euclidien est un espace elliptique. La distance d'un espace elliptique peut s'exprimer à l'aide de la quadrique imaginaire et des birapports.

• La géométrie sphérique peut être obtenue de la géométrie affine de la manière suivante. On fixe la sphère unité S de Rⁿ. Alors le groupe orthogonal est le groupe des transformations affines (ou linéaires) de Rⁿ qui laissent stable S, et alors le groupe des isométries de S est le groupe des transformations de S induites par le groupe orthogonal.

• On peut interpréter la géométrie hyperbolique en termes de géométrie projective. On prend comme espace l'espace hyperbolique) comme l'intérieur H d'une quadrique ovale Q d'un espace projectif réel P de dimension n (l'intérieur d'une conique projective d'un plan projectif réel, par exemple) et dont le groupe est le groupe de transformations de H obtenu par restriction à H des éléments du sous-groupe du groupe projectif de P qui laissent stable H (on obtient le groupe des isométries de l'espace hyperbolique H). On dit que la quadrique ovale Q est l'absolu de l'espace hyperbolique H C'est le modèle projectif de Klein de la géométrie hyperbolique. On peut exprimer la distance d'un espace hyperbolique à l'aide de Q et des birapports.

• Il y a aussi la géométrie de Möbius (ou géométrie conforme). En part du même espace projectif P et de la même quadrique Q que dans la cas de la géométrie hyperbolique. On prend comme espace la quadrique ovale Q de P et on prend comme groupe le groupe des transformations de Q obtenue par restriction à Q des éléments du groupe projectif de P qui laissent stable Q.

• L'espace de la géométrie de Möbius avec son groupe est essentiellement équivalent (si n est supérieur à 3) à une sphère euclidienne avec comme groupe non pas son groupe des isométries (le groupe orthogonal vu plus haut), mais un groupe qui le contient strictement : c'est son groupe conforme (ou groupe de Möbius), c'est-à-dire le groupe des transformations de la sphère qui envoient les cercles sur des cercles (ou encore le groupe des difféomorphismes de cet sphère qui préservent les angles des courbes tracées sur cette sphère). Pour le voir, il suffit de voir que le complété projectif d'une sphère euclidienne est une quadrique ovale d'un espace projectif (il n'y a pas de points à l'infini à une sphère euclidienne).

• L'espace de la géométrie de Möbius avec son groupe est aussi essentiellement équivalent à l'espace obtenu en ajoutant un point à l'infini à un espace euclidien X (son compactifié d'Alexandrov) et en considérant le groupe de transformations engendré par les réflexions de X par rapport à des hyperplans affines de X et par les inversions de X par rapport à des sphères X. Pour le voir, il suffit de se ramener à une sphère euclidienne à l'aide d'une projection stéréographique. Alors, le stabilisateur du point à l'infini de X pour ce groupe induit sur X le groupe des similitudes affines de X, et on obtient alors la géométrie euclidienne semblable.

Pour inclure une plus grande classe d'objets, il est souhaitable d'étendre la définition d'invariants. Il peut être intéressant de porter l'étude sur des ensembles de parties globalement invariants par l'action induite du groupe. Ainsi les quadriques ovales (ou les coniques propres) forment un ensemble de parties d'un espace projectif réel (ou d'un plan projectif réel) invariant par le groupe projectif.

Il faut remarquer qu'à deux types de géométrie peuvent correspondre des groupes isomorphes, sans que les géométries soient équivalentes. Voici deux exemples.

• À la géométrie de la sphère orientée et à l'espace projectif est associé, en dimension paire le même groupe, à savoir SO_{n + 1}(R). Cependant ces géométries sont à rapprocher : on dit aujourd'hui que Sⁿ est le revêtement universel de P_nR, revêtement à deux feuillets.

• De même, les groupes de la géométrie hyperbolique et de la géométrie conforme sont isomorphes (ils sont induits par le même sous-groupe du groupe projectif), mais les espaces ne sont pas isomorphes : un espace hyperbolique est homéomorphe à un espace affine euclidien (donc non compact), alors que l'espace de la géométrie conforme est homéomorphe à une sphère euclidienne (donc compact). Il y a toutefois un lien entre ces géométries : la géométrie conforme est l'absolu de la géométrie hyperbolique.