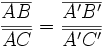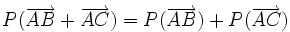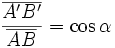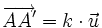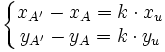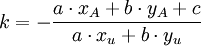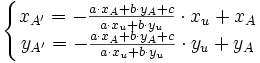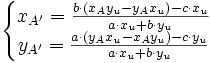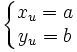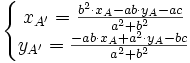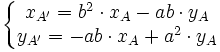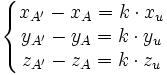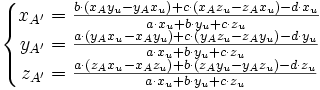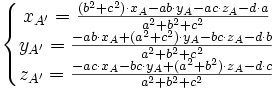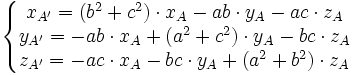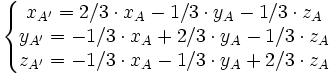Projection (géométrie) - Définition

Introduction

En géométrie, une projection est une transformation de l'espace, c'est-à-dire une application linéaire qui projette l'espace sur une sous partie. Par exemple pour faire de la 3D on projette l'espace (en 3D) sur l'écran (en 2D), on obtient ainsi un rendu similaire à celui que l'on aurait eu en regardant la même scène avec ses propres yeux.

Projection en géométrie plane

En géométrie plane, on considère une droite D du plan et une direction Δ non parallèle à D. Soit un point A du plan, alors la projection de A sur D selon Δ est le point A' = P(A) tel que :

• Si A est sur D, alors A = A' ;
• sinon :
  • A' est situé sur D ;
  • la droite (AA' ) est parallèle à Δ.

En géométrie euclidienne, on fait fréquemment usage d'un cas particulier de projection linéaire, la projection orthogonale : c'est le cas particulier où Δ est perpendiculaire à D. Dans ce cas-là, si A est hors de D, alors (AA') est perpendiculaire à D.

La projection est une application linéaire. Cela signifie que si A, B et C sont trois points alignés et si A', B' et C' sont leurs projetés, alors

(on oriente les droites) ou encore

et si k est un scalaire, alors

.

Projections et coordonnées cartésiennes

Les droites D et Δ se coupent en O. Alors, soient A' le projeté de A sur D parallèlement à Δ, et A'' le projeté de A sur Δ parralèllement à D. On voit que et définissent des coordonnées cartésiennes de A dans le repère (O, D, Δ), les droites D et Δ étant orientées et normées.

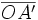
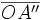
Projection et trigonométrie

Considérons une projection orthogonale sur D. Soient deux point A et B, et soit α l'angle . Alors

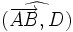
Projection parallèlement à une droite en géométrie analytique

Soit un vecteur directeur de Δ de composantes (x_u, y_u). Soit

a·x + b·y + c = 0

l'équation de D. Soit le point A de coordonnées (x_A, y_A) et son projeté A' de coordonnées (x_A', y_A').

Comme (AA' ) est parallèle à Δ, il existe un scalaire k tel que

soit

Par ailleurs, A' est sur D, ce qui signifie que

a·x_A' + b·y_A' + c = 0

on obtient donc

a·(k·x_u + x_A) + b·(k·y_u + y_A) + c = 0

d'où

(a·x_u + b·y_u est non nul puisque n'est pas colinéaire à D) d'où

soit

Dans le cas d'une projection orthogonale, et si le repère est orthonormé, alors on peut choisir

ce qui donne

on peut alors vérifier que si l'on prend la projection orthogonale sur l'axe Ox (qui a pour équation y = 0 soit a = c = 0 et b = 1), on a bien x_A' = x_A et y_A' = 0.

Si l'on décide arbitrairement que D contient l'origine (c = 0) et que a² + b² = 1, on obtient alors

Définition générale

En algèbre linéaire une projection est une application naturellement associée à une décomposition de l'espace sous forme de deux sous-espaces supplémentaires. À un vecteur de l'espace, elle associe l'un des deux éléments de sa décomposition sur ces deux espaces.

Voir l'article détaillé Projecteur (mathématiques).

À ce titre, la projection centrale n'est pas un projecteur.

Projection en géométrie dans l'espace

Projection sur un plan parallèlement à une droite

Considérons un plan Π et une droite Δ. Soit A un point de l'espace. La projection P sur Π parallèlement à Δ est définie par :

• P(A) est sur Π ;
• si A est sur Π, alors P(A) = A ;
• sinon, la droite (A, P(A)) est parallèle à Δ.

Si Δ est perpendiculaire à Π, alors la projection est dite orthogonale.

La projection est une application linéaire, on retrouve donc des propriétés de la projection en géométrie plane : si A, B et C sont trois points alignés et si A', B' et C' sont leurs projetés, alors

(on oriente les droites) ou encore

et si k est un scalaire, alors

.

Projection sur un plan parallèlement à une droite en géométrie analytique

Soit un vecteur directeur de Δ de composantes (x_u, y_u, z_u). Soit

a·x + b·y + c·z + d = 0

l'équation de Π. Soit le point A de coordonnées (x_A, y_A, z_A) et son projeté A' de coordonnées (x_A', y_A', z_A').

Comme (AA' ) est parallèle à Δ, il existe un scalaire k tel que

soit

Par ailleurs, A' est sur Π, ce qui signifie que

a·x_A' + b·y_A' + c·z_A' + d = 0

On voit que d'un point de vue analytique, le problème est très similaire au précédent. On a un système de quatre équations à quatre inconnues x_A', y_A', z_A' et k. On obtient :

Dans le cas d'une projection orthogonale et si le repère est orthonormal, on peut choisir x_u = a, y_u = b et z_u = c, soit

Si l'on décide arbitrairement que Π contient l'origine (d = 0) et que a² + b² + c² = 1, alors on a

Dans le cas de la perspective isométrique, on choisit |a| = |b| = |c| = 1/√3. Par exemple, si on choisit les trois valeurs positives, on a

Projection sur une droite parallèlement à un plan

Avec les mêmes notations que ci-dessus, on peut définir la projection Q sur Δ parallèlement à Π :

• Q(A) est sur Δ ;
• si A est sur Δ, alors Q(A) = A ;
• sinon, la droite (A, Q(A)) est coplanaire à Π.

Si Δ est perpendiculaire à Π, alors la projection est dite orthogonale.

C'est toujours une applicaiton linéaire, elle a donc les propriétés énoncées ci-dessus.

Projections et coordonnées cartésiennes

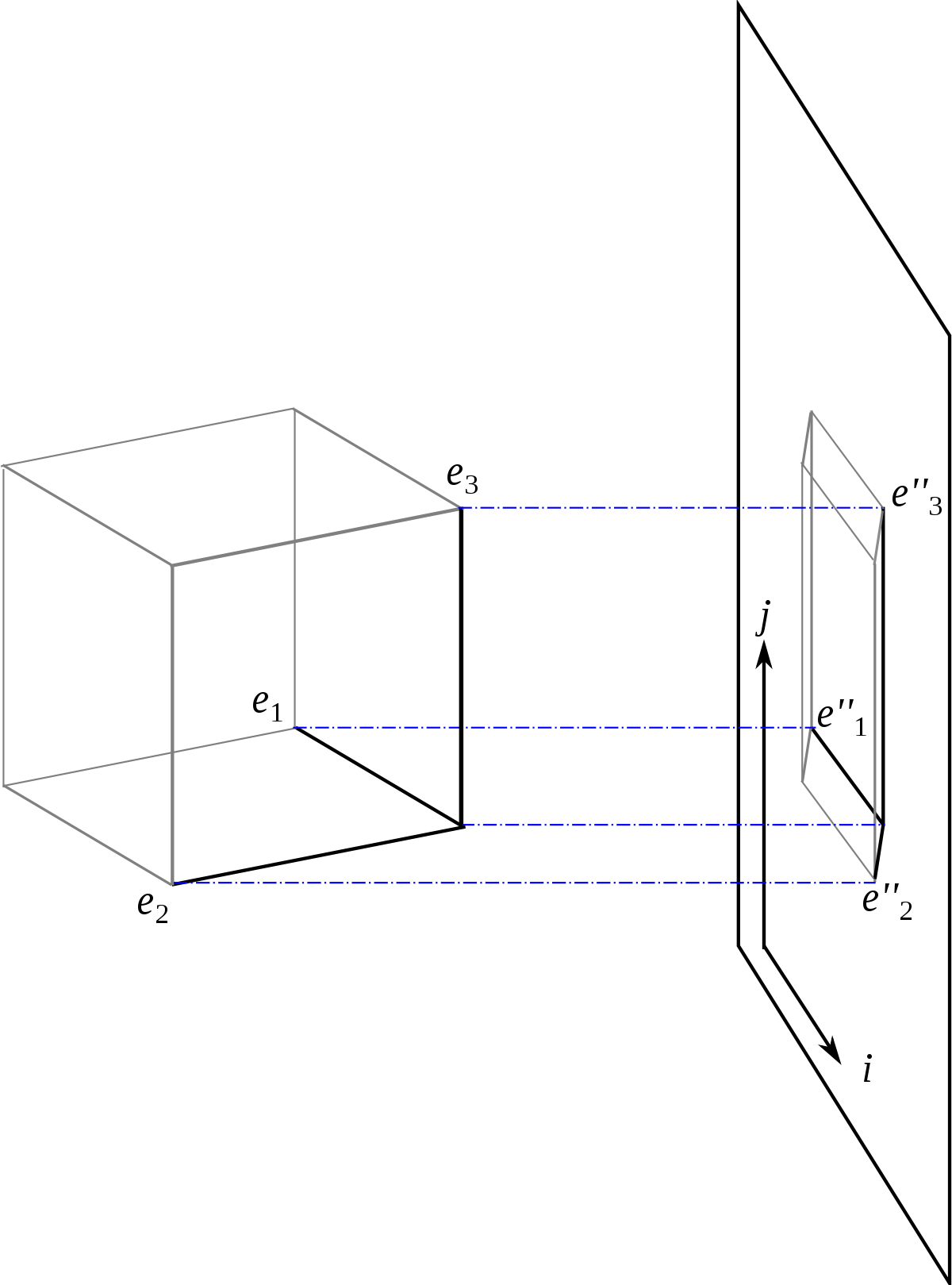
Considérons trois droites D₁, D₂ et D₃, non coplanaires et concourante en un point O. Elles sont normées et orientées.

Pour un point de l'espace A, on appelle :

• A₁ le projetté de A sur D₁ parallèlement au plan (D₂, D₃) ;
• A₂ le projetté de A sur D₂ parallèlement au plan (D₃, D₁) ;
• A₃ le projetté de A sur D₃ parallèlement au plan (D₁, D₂).

Alors, (O,D₁, D₂, D₃) forme un repère et sont les coordonnées de A dans ce repère.

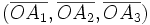
Projection centrale

En géométrie projective, on considère des projections centrales. Elles décrivent ce qui arrive aux positions observées de différents objets quand l'œil de l'observateur change de place. Les transformations projectives en sont la généralisation.