Raisonnement par récurrence - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le raisonnement par récurrence est une forme de raisonnement visant à démontrer une propriété portant sur tous les entiers naturels. Le raisonnement par récurrence consiste à démontrer les points suivants :
- Une propriété est satisfaite par l'entier 0 ;
- Si cette propriété est satisfaite par un certain nombre entier naturel n, alors elle doit être satisfaite par son successeur, c'est-à-dire, le nombre entier n+1.
Une fois cela établi, on en conclut que cette propriété est vraie pour tous les nombres entiers naturels.
Présentation
Le raisonnement par récurrence établit une propriété importante liée à la structure des entiers naturels : celle d'être construits à partir de 0 en itérant le passage au successeur. Dans une présentation axiomatique des entiers naturels, il est directement formalisé par un axiome. Moyennant certaines propriétés des entiers naturels, il est équivalent à d'autres propriétés de ceux-ci, en particulier l'existence d'un minimum à tout ensemble non vide (bon ordre), ce qui permet donc une axiomatisation alternative reposant sur cette propriété.
Certaines formes de ce raisonnement se généralisent d'ailleurs naturellement à tous les bons ordres infinis (pas seulement celui sur les entiers naturels), on parle alors de récurrence transfinie, de récurrence ordinale (tout bon ordre est isomorphe à un ordinal) ; le terme d’induction est aussi souvent utilisé dans ce contexte. Le raisonnement par récurrence peut se généraliser enfin aux relations bien fondées. Dans certains contextes, logique mathématique ou en informatique, pour des structures de nature arborescente ou ayant trait aux termes du langage formel sous-jacent, on parle de récurrence structurelle.
On parle communément de récurrence dans un contexte lié mais différent, celui des définitions par récurrence de suites (ou d'opérations) à argument entier. Si l'unicité de telles suites se démontre bien par récurrence, leur existence, qui est le plus souvent tacitement admise dans le secondaire, voire les premières années universitaires, repose sur un principe différent.
Récurrence simple sur les entiers
Pour démontrer une propriété portant sur tous les entiers naturels, comme par exemple la formule du binôme de Newton, on peut utiliser un raisonnement par récurrence. Notons la propriété en question P(n) pour indiquer la dépendance en l'entier n. On peut alors l'obtenir pour tout entier n en démontrant ces deux assertions :
- P(0) (0 vérifie la propriété) : c'est l'initialisation de la récurrence ;
- Pour tout entier n, (P(n) ⇒ P(n+1)) : c'est l'hérédité.
On dit alors que la propriété P s'en déduit par récurrence pour tout entier n. On précise parfois « récurrence simple », quand il est nécessaire de distinguer ce raisonnement d'autres formes de récurrence (voir la suite).
Le raisonnement par récurrence est une propriété fondamentale des entiers naturels, et c'est le principal des axiomes de Peano. Une axiomatique est, en quelque sorte une définition implicite, dans ce cas une définition implicite des entiers naturels. Dans certains contextes, comme en théorie des ensembles on déduit directement la récurrence de la définition, explicite cette fois, de l'ensemble des entiers naturels.
La récurrence peut aussi s'exprimer de façon ensembliste : il s'agit juste d'une variation sur la définition d'un ensemble en compréhension. On associe à une propriété P l'ensemble E des entiers naturels la vérifiant, et à un ensemble d'entiers naturels E la propriété d'appartenance associée. La récurrence se réénonce alors de façon équivalente ainsi :
- Soit E un sous-ensemble de N, si :
- 0 appartient à E
- Pour tout entier naturel n, (n appartient à E implique n+1 appartient à E)
- Alors E = N.
Bien sûr, l'initialisation peut commencer à un entier k arbitraire et dans ce cas la propriété n'est démontrée vraie qu'à partir du rang k :
- Si :
- P(k) ;
- Pour tout entier n supérieur ou égal à k, [P(n) implique P(n+1)] ;
- Alors pour tout entier n supérieur ou égal à k, P(n).
Cette récurrence à partir de k est une conséquence immédiate de la récurrence à partir de 0 : il suffit de démontrer « n < k ou P(n) », ou encore « P(n+k) » si l'on dispose de l'addition, par récurrence sur n ; chacune de ces propriétés est bien vraie pour tout entier n si et seulement si la propriété P est vraie pour tout entier supérieur ou égal à k.
De façon analogue on aura d'autres raisonnements par récurrence, sans avoir besoin de poser à chaque fois un nouveau principe, par exemple, une récurrence sur les entiers pairs (prendre P(2n)), etc.
Exemple 1 : la somme des n premiers entiers impairs
Les entiers impairs sont les entiers de la forme 2n+1 (le premier, obtenu pour n=0, est 1). On déduit d'une identité remarquable bien connue que 2n+1 ajouté au carré de n donne le carré du nombre suivant :
- n2+2n+1 = (n+1)2
On va donc montrer par récurrence que la somme des n premiers entiers impairs est égale au carré de n :
- 1+3+ … + (2n-1) = n2.
Bien que l'écriture précédente puisse laisser entendre que 2n -1 > 3, on ne le supposera pas. La somme est vide donc nulle si n = 0, réduite à 1 si n=1, égale à 1+3 si n=2 etc.
- initialisation : le cas n=0 est celui où la somme est vide, elle est donc bien égale à 02
- hérédité : pour un entier n arbitraire, on suppose que 1+3+ … + (2n-1) = n2. Puisque l'entier impair qui suit 2n-1 est 2n+1, on en déduit que :
-
- 1+3+ … + (2n-1) + (2n+1) = n2+2n+1= (n+1)2,
- c'est-à-dire que la propriété est héréditaire.
Exemple 2 : Identité du binôme de Newton
Précautions à prendre
- L’initialisation ne doit pas être oubliée. Voici un exemple un peu ad hoc mais qui illustre bien ceci. On montre facilement que les propriétés « 32n+6 - 2n est un multiple de 7 » et « 32n+4 - 2n est un multiple de 7 » sont toutes deux héréditaires. Cependant la première est vraie pour tout entier naturel n, alors que la seconde ne l'est pas car elle n’est jamais initialisable : en effet, en n=0 on a 34 - 1 = 80, qui n'est pas divisible par 7. Pour la première proposition :
-
- on vérifie que si n = 0, 36 - 20 est bien un multiple de 7 (728 est bien un multiple de 7) ;
- on montre que si 32n+6 - 2n est un multiple de 7, alors 32n+8 - 2n+1 est un multiple de 7 :
-
-
![3^{2n+8} - 2^{n+1}\begin{array}[t]{l}= 9\times 3^{2n+6} - 2 \times 2^{n}\\ = (7+2)\times 3^{2n+6} - 2 \times 2^{n}\\ = 7\times 3^{2n+6} +2\times 3^{2n+6} - 2 \times 2^{n}\\ = 7\times 3^{2n+6} +2( 3^{2n+6} -2^{n}) \end{array}](https://static.techno-science.net/illustration/Definitions/autres/7/7dd844c069ddc213c0cba17d5c3376ec_3a20d002578c88115b845ee4076a4ccd.png)
-
- 32n+6 - 2n est donc somme de deux multiples de 7, c’est bien un multiple de 7.
- L'hérédité de la seconde propriété est strictement analogue. On montre pourtant, en utilisant les congruences modulo 7, qu'elle n'est vraie pour aucun entier (congruences que l'on pourrait d'ailleurs utiliser également pour démontrer la première propriété).
![3^{2n+8} - 2^{n+1}\begin{array}[t]{l}= 9\times 3^{2n+6} - 2 \times 2^{n}\\ = (7+2)\times 3^{2n+6} - 2 \times 2^{n}\\ = 7\times 3^{2n+6} +2\times 3^{2n+6} - 2 \times 2^{n}\\ = 7\times 3^{2n+6} +2( 3^{2n+6} -2^{n}) \end{array}](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/7dd844c069ddc213c0cba17d5c3376ec_3a20d002578c88115b845ee4076a4ccd.png)
- L’hérédité doit être démontrée pour tout entier n plus grand ou égal au dernier n₀ pour lequel la propriété a été démontrée directement (initialisation).
- Si on prend, par exemple, la suite
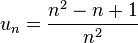
. - Si on cherche à démontrer que
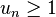
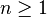
- l’initialisation est facile à prouver car u1 = 1.
- l’hérédité aussi car, la suite étant croissante, si
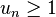
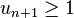
- Pourtant cette inégalité est vraie seulement pour n = 1. L’hérédité n’a en réalité été prouvée que pour n supérieur ou égal à 2 et non pour n supérieur ou égal à 1.
