Spin - Définition

Spin des particules usuelles

Comme la plupart des observables, le spin est représentable par un vecteur dont toute mesure est quantifiée (les mesures donnent des valeurs discontinues), et surtout le principe d'incertitude s'applique aux mesures du spin faites dans les différentes directions de l'espace : on peut mesurer précisément la norme du vecteur et une projection sur un axe de coordonnées, mais les deux autres projections sur les deux autres axes ne sont plus alors mesurables. Mathématiquement, cela est dû au fait que les trois opérateurs de projections du spin , , ne commutent pas entre eux, mais tous commutent avec l'opérateur de la norme (au carré).

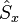
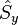
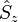
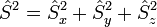
Les propriétés algébriques des opérateurs du spin impliquent qu'il existe un nombre s dit entier ou « demi-entier », c-est-à-dire pris dans l'ensemble {0, 1/2, 1, 3/2, 2, ...} et nommé spin, tel que la mesure de la norme du vecteur donne et que la mesure de la projection du vecteur sur un axe quelconque donne un résultat parmi les 2 s + 1 valeurs possibles .

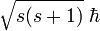
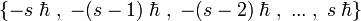
Pour une raison assez complexe démontrée dans le cadre de ce qui est appelé théorème spin-statistique, le valeur entière ou demi-entière du spin détermine une propriété cruciale de la particule : si son spin est entier, c'est un boson, si son spin est demi-entier, c'est un fermion.

La totalité des particules connues ou d'existence fortement suspectée a un spin compris entre 0 et 2. En particulier

• Spin 0 : le boson de Higgs, particule hypothétique, non encore découverte expérimentalement.
• Spin 1/2 : l'électron, le positron, le proton, le neutron, les neutrinos, les quarks, etc.
• Spin 1 : le photon, les bosons W^± et Z⁰, vecteurs de l'interaction faible.
• Spin 2 : le graviton, particule hypothétique vecteur de la gravitation.

Il n'existe pas de particule élémentaire connue de spin 3/2, mais la supersymétrie, si elle existe, en prédit une, le gravitino.

Le spin de particules composées de plusieurs particules élémentaires, comme le proton, le neutron, tout noyau atomique ou atome, est constitué des spins des particules qui les composent auxquels s'ajoute leur éventuel moment angulaire orbital.

« Rotation propre »

Historiquement, le spin a d'abord été interprété par Samuel Goudsmit et George Uhlenbeck en septembre 1925 comme étant un moment cinétique intrinsèque, c'est-à-dire dû à une rotation de la particule sur elle-même. Cette vision classique d'une rotation propre de la particule est en fait trop naïve. En effet, si la particule est ponctuelle, la notion de rotation propre autour de son axe est tout simplement dénuée de sens physique.

Si à l'inverse la particule n'est pas ponctuelle, alors la notion possède un sens, mais on se heurte dans ce cas à d'autres difficultés, notamment cela impliquerait que la particule ait une vitesse de rotation, à son équateur, strictement supérieure à la vitesse de la lumière.

En effet, supposons par exemple que la particule soit un électron, modélisé comme étant un corps sphérique de rayon a. On obtient une estimation de ce rayon en écrivant que l'énergie de masse de l'électron est de l'ordre de grandeur de son énergie potentielle électrostatique, soit :

, où q est la charge électrique de l'électron, m sa masse, c la vitesse de la lumière et ε la permittivité du vide. La valeur numérique de ce rayon classique de l'électron est de l'ordre de 10^-15 mètre. Si l'on attribue alors à cet électron un moment cinétique égal à , on obtient pour un point de l'équateur une vitesse v vérifiant :

,

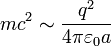
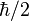
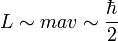
ce qui, en combinant avec l'équation précédente donne

,

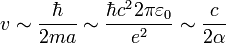
où l'on a introduit la constante de structure fine α. α étant bien plus petite que 1, la valeur obtenue de la vitesse est très supérieure à celle de la lumière, en contradiction avec la relativité restreinte.

De fait, aucune description purement mécanique de la nature du spin n'est en mesure de rendre compte des propriétés observées. En particulier il est difficile de conceptualiser à quoi un spin demi-entier peut correspondre pour une particule élémentaire.