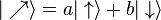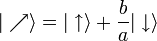Spin - Définition
La liste des auteurs de cet article est disponible ici.
Historique
Le spin de l'électron a été expérimentalement mis en évidence en 1922 dans l'expérience de Stern et Gerlach et a d'abord été interprété comme une rotation de la particule autour d'un axe (comme son nom l'indique en anglais) en 1923 par George Uhlenbeck et Samuel Goudsmit, mais Wolfgang Pauli a montré en 1924 que, compte tenu des dimensions connues de l'électron, cela nécessitait une vitesse de rotation à son équateur qui serait supérieure à la vitesse de la lumière. Dès lors la représentation du spin en termes de rotation n'a plus été utilisée en dehors d'un cadre de vulgarisation.
La notion théorique de spin a été introduite par Pauli en décembre 1924 pour l'électron, afin d'expliquer un résultat expérimental qui restait incompréhensible dans le cadre naissant de la mécanique quantique non relativiste : l'effet Zeeman anomal. L'approche développée par Pauli consistait à introduire de façon ad-hoc le spin en ajoutant un postulat supplémentaire aux autres postulats de la mécanique quantique non relativiste (équation de Schrödinger, etc.).
En 1927, Wolfgang Pauli a proposé la modélisation du spin en termes de matrices, ce qui correspond à une écriture en termes d'opérateurs sur la fonction d'onde intervenants dans l'équation de Schrödinger : l'équation de Pauli. En 1928, à partir de l'équation de Klein-Gordon, Paul Dirac démontra qu'une particule ayant un spin non-nul vérifie une équation relativiste, appelée aujourd'hui équation de Dirac.
Enfin, c'est en théorie quantique des champs que le spin montre son caractère le plus fondamental. L'analyse du groupe de Poincaré effectuée par Wigner en 1939 montra en effet qu'une particule est associée à un champ quantique, opérateur qui se transforme comme une représentation irréductible du groupe de Poincaré. Ces représentations irréductibles se classent par deux nombres réels positifs : la masse et le spin.
Le spin du photon a été découvert expérimentalement par Raman et Bhagavantam en 1931.
Formalisme de Pauli
Opérateur spin
En mécanique quantique, le spin est un opérateur vectoriel hermitien comportant trois composantes, notées usuellement
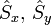
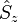
où εijk est le symbole de Levi-Civita. Ces relations de commutations sont analogues à celles découvertes en novembre 1925 par Born, Heisenberg et Jordan pour les composantes du moment cinétique orbital :
![\left[ \, \hat{L}_i \, , \ \hat{L}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{L}_k](https://static.techno-science.net/illustration/Definitions/autres/5/50b2055de1bf66ce973994caf003e045_e524276fd2acaeceb4bef62a2b48319c.png)
Par analogie avec les résultats obtenus pour le moment cinétique orbital (ou plus généralement pour un moment cinétique quantique), il existe pour l'opérateur spin une base de vecteurs propres notés | s,ms > , où s est entier ou demi-entier, et ms est un entier ou demi-entier prenant l'une des 2s + 1 valeurs
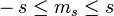
Spin 1/2 - matrices de Pauli
Pour une particule de spin 1/2 comme l'électron, on a s = 1 / 2, donc 2s + 1 = 2 : il existe seulement deux états de spin distincts, caractérisés par
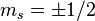
On note souvent les deux états propres correspondant :
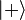
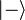
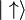
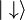
Pauli a introduit trois matrices 2 x 2, notées
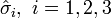
Ces trois matrices de Pauli s'écrivent explicitement :
Elles satisfont les relations de commutation :
Représentation géométrique du spin par une sphère de Riemann
Un état quantique quelconque d'une particule de spin 1/2 peut s'exprimer sous la forme générale :
(a et b étant deux nombres complexes). Cette formule exprime une superposition des deux états propres.
Selon les règles de la mécanique quantique, l'état quantique représenté par

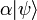
L'état de spin 1/2 est donc entièrement caractérisé par un nombre complexe
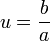
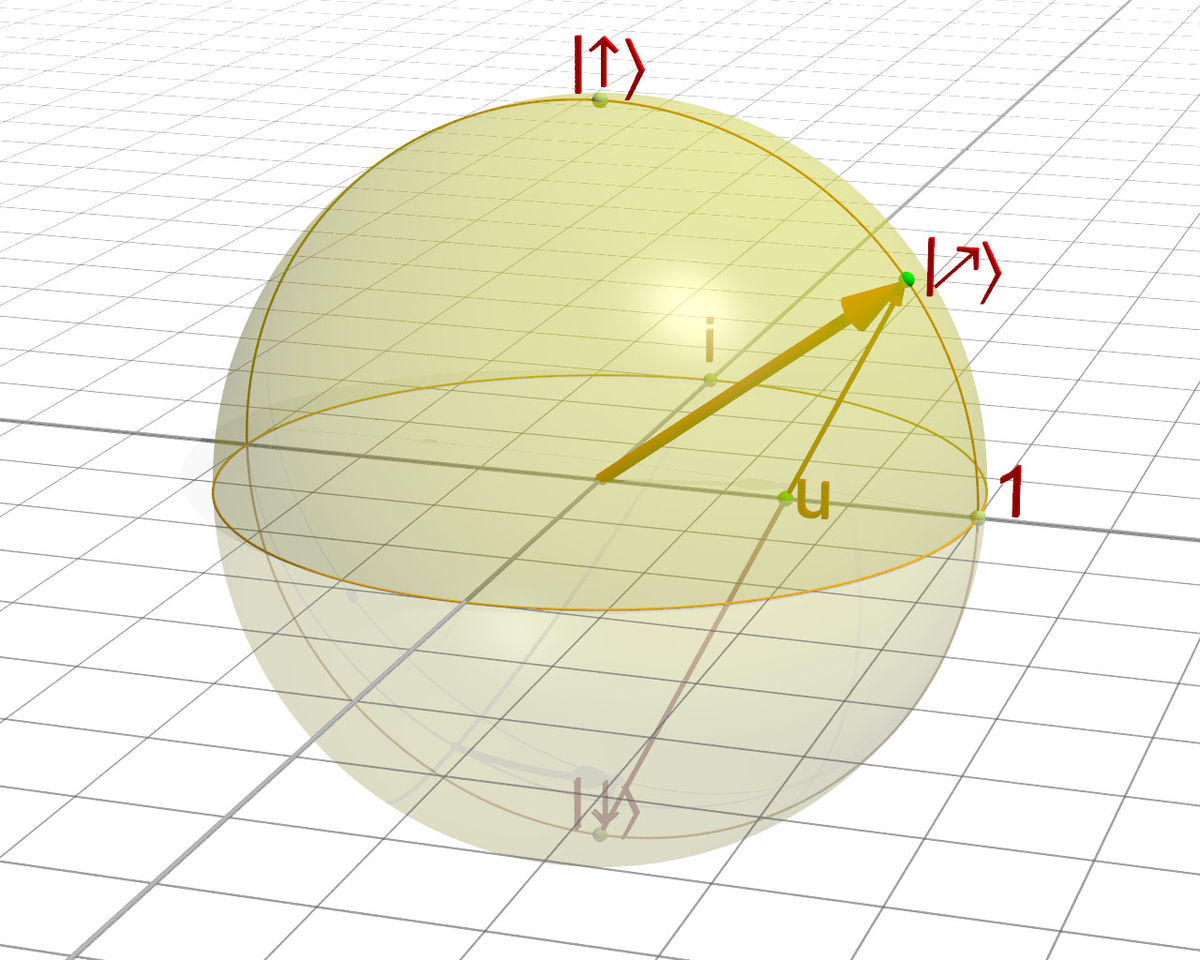
Selon cette représentation, tout état de spin 1/2 trouve une représentation géométrique (voir figure ci-contre). Le vecteur passant par l'origine et pointant sur la projection du complexe u sur la sphère de Riemann donne une visualisation géométrique de l'état de spin 1/2 comme étant une direction dans l'espace.
Bien que semblant a priori purement mathématique, cette représentation de l'état de spin comme étant une direction dans l'espace possède une certaine pertinence. Notamment, on peut retrouver simplement à l'aide de cette représentation géométrique la probabilité d'obtenir l'état
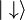
![\left[ \, \hat{S}_i \, , \ \hat{S}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{S}_k](https://static.techno-science.net/illustration/Definitions/autres/5/56736a4c37a2470ddb3bc4bf03c15bab_cad961c5e0499e2ad612700161c13ae0.png)
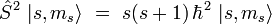
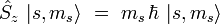
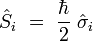
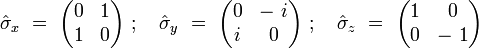
![\left[ \, \hat{\sigma}_i \, , \ \hat{\sigma}_j \, \right] \ = \ 2 \ i \ \epsilon_{ijk} \ \hat{\sigma}_k](https://static.techno-science.net/illustration/Definitions/autres/f/f0e84d8251c96b1f008b317be9a55e54_cf13755f1854e8e64745a5d1e50a84b7.png)