Temps (physique) - Définition

Le temps dans différents domaines de la physique

Utilisation de la vitesse de la lumière

La vitesse limite ne pouvant être dépassée est (jusqu'à preuve du contraire) égale à c, c'est-à-dire la vitesse de la lumière dans le vide (soit 299 792 458 mètres par seconde), une des constantes de l'univers physique. Cette vitesse intervient directement dans des phénomènes physiques courants, à savoir en l'occurrence la propagation dans le vide des ondes électromagnétiques dont fait partie la lumière; la propagation de ces ondes dans l'air se faisant à une vitesse légèrement plus faible mais encore proche de c. C'est pourquoi on l'utilise parfois comme unité de référence pour exprimer des vitesses, exprimer ou mesurer des distances très grandes (la distance de la Terre au Soleil est de 150 millions de km ou 8 minutes-lumière). Les mesures exactes de durées et les corrections aux calculs qui s'y rapportent conformément à la théorie de la relativité sont nécessaires au fonctionnement des systèmes de positionnement comme le GPS, à cause de la précision très grande requise sur les mesures de temps sur lesquelles ils reposent (les temps d'arrivée de signaux électromagnétiques de satellites permettant de calculer les distances à ces satellites et donc la position).

Ainsi, la seconde est définie comme égale à 9 192 631 770 périodes de la radiation de transition entre les deux niveaux hyperfins d'énergie de l'état fondamental de l'atome de césium 133; elle sert de base à la définition de l'unité d'espace (le mètre, défini comme distance parcourue par la lumière dans le vide en 1/299 792 458 seconde).

Physique Newtonienne et temps linéaire

Voir physique classique

Vers 1665, lorsque Isaac Newton tira de la chute des corps sous l'influence de la gravité, la première formulation claire de physique mathématique du traitement du temps : temps linéaire, conçu comme une horloge universelle.

Thermodynamique et le paradoxe d'irréversibilité

1812 - Fourier publie sa Théorie analytique de la chaleur. 1824 - Sadi Carnot analysa scientifiquement le moteur à vapeur

1^re loi de la thermodynamique - ou loi de conservation de l' énergie

2nde loi de la thermodynamique - la loi d'entropie (1850 - Clausius)

E = ... (énergie thermique)

ds = ...

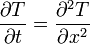
Les équations thermodynamiques, et en particulier la notion d'entropie, donnent au temps un sens, en introduisant la nécessité de l'irréversibilité. L'entropie d'un système isolé ne peut être que croissante au cours du temps.

La physique d'Einstein et le temps

Avant Einstein

Avec Einstein

En physique des particules

Méta

En 1875, Lorentz découvrit la transformation de Lorentz, découverte aussi en 1887 par W. Voigt, dont on se sert dans la théorie de la relativité restreinte d'Einstein publiée en 1905, au lieu des équations de transformation de Galilée. Cette théorie est basée sur le postulat que la vitesse de la lumière est la même quel que soit le référentiel d'inertie à partir duquel on la calcule.

La théorie de la relativité d'Einstein utilise la géométrie de Riemann, qui emploie le tenseur métrique décrivant l'espace de Minkowski : [(dx₁)² + (dx₂)² + (dx₃)² − c²(dt)²)], pour développer une solution géométrique à la transformation de Lorentz qui préserve les équations de Maxwell.

La théorie d'Einstein est basée sur l'hypothèse que tous les référentiels d'inertie sont équivalents en ce qui concerne toutes les lois de la physique. Sa théorie, simple et élégante, montre que la mesure du temps est différente d'un référentiel d'inertie à l'autre, c'est-à-dire qu'il n'existe pas de temps universel et unique. Chaque référentiel d'inertie possède sa propre mesure du temps.

Physique quantique et temps

Voir aussi mécanique quantique.

L'une des inégalités de Heisenberg, , lie l'incertitude sur le temps de vie d'un système quantique et la mesure de son énergie. Pour simplifier, plus on connaît l'énergie d'une particule avec précision, moins on sait la situer dans le temps, et plus on en sait sur sa position dans le temps, moins on connaît son énergie. Cette inégalité peut avoir des conséquences remarquables, notamment en physique des particules : les interactions entre particules, assimilables (en première approximation) à des chocs, sont si brèves que l'incertitude sur l'énergie échangée est très grande. En fait, le terme incertitude est lui-même impropre, voir à ce sujet l'article concernant le principe d'incertitude. Or, comme d'après la célèbre équation E=mc², la masse est liée à l'énergie en jeu, de nouvelles particules peuvent apparaître de cette énergie, qui d'un point de vue extérieur semble venir de nulle part.

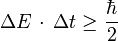
Systèmes dynamiques

Voir systèmes dynamiques et théorie du chaos, structures dissipatives

On pourrait dire que le temps est la paramétrisation d'un système dynamique qui permet de révéler et d'agir sur la géométrie du système. Il a été affirmé que le temps est une conséquence implicite du chaos (c'est-à-dire sa non-linéarité/ son irréversibilité): le temps caractéristique, d'un système. Benoit Mandelbrot introduit le temps intrinsèque dans son livre Multifractales and bruit 1/f.