Théorème d'Ascoli - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En analyse fonctionnelle, le théorème d'Ascoli est un puissant résultat caractérisant les parties relativement compactes de l'espace des fonctions continues définies sur un espace compact à valeurs dans un espace métrique. Il se généralise sans difficulté au cas où l'espace de départ est seulement localement compact.
Ce théorème est connu pour son nombre considérable d'applications (complétude de certains espaces fonctionnels, compacité de certains opérateurs, dépendance en les conditions initiales dans les équations différentielles ...).
Énoncé
Dans un espace vectoriel normé de dimension finie, les parties compactes sont exactement les parties fermées et bornées. Dans un espace vectoriel topologique séparé, les parties relativement compactes restent bornées ; mais la réciproque est fausse. Le théorème d'Ascoli traite du cas de l'espace des fonctions continues :
Soient
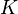
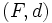
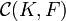
Une partie A de
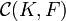
- A est équicontinue, i.e pour tout
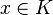

- Pour tout
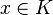
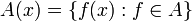
Un ensemble de fonctions r-lipschitziennes est un exemple d'ensemble équicontinu.
Il existe de nombreuses variantes du théorème d'Ascoli.
Démonstration
Le théorème d'Ascoli établit une équivalence. Les deux implications sont démontrées séparément. Les notations sont celles de l'énoncé ci-dessus.
Condition nécessaire
Notons B l'adhérence de A dans
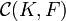
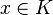
Pour montrer que A(x) est relativement compact dans F, il suffit de remarquer qu'il est inclus dans B(x) qui est compact, comme image du compact B par l'application continue de C(K,F) dans F qui à f associe f(x).
Montrons maintenant l'équicontinuité de B au point x (qui entraînera celle de A). Soit

Par précompacité de B, il existe un nombre fini d'éléments
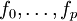
Par continuité en x de
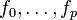
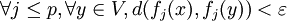
Pour toute fonction f dans B et tout point y dans V, l'inégalité triangulaire donne :
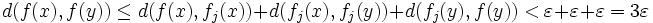
d'où l'équicontinuité de B.
Condition suffisante
La réciproque est le sens le plus souvent utilisé et demande plus d'attention. On souhaite démontrer qu'une partie équicontinue A de C(K,F) telle que A(x) soit relativement compacte pour tout x, est incluse dans un compact de C(K,F).
Notons C l'adhérence de A dans l'espace FK des applications de K dans F muni de la topologie de la convergence simple (autrement dit, FK est muni de la topologie produit). D'après les propriétés de l'équicontinuité, C est encore équicontinu, et les deux topologies sur C induites par son inclusion dans C(K,F) et dans FK coïncident. Il suffit donc de prouver que C est un compact de FK.
Introduisons le sous-espace
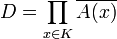
Condition suffisante, seconde preuve
Une alternative à l'utilisation du théorème de Tychonov est de prouver élémentairement que l'adhérence B de A dans C(K,F) est précompacte et complète (donc compacte), de la façon suivante.
Montrons d'abord que A est précompact (donc B aussi). Soit ε > 0, montrons que A est recouvert par une famille finie d'ensembles Cj de diamètres
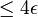
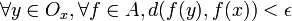
Par compacité de K, il existe alors une partie finie
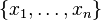
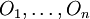
Posons
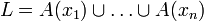
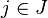
Notons enfin, pour tout
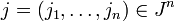
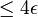
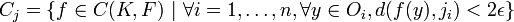
Il reste à prouver que les Cj recouvrent A. Soit
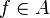
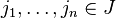
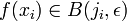
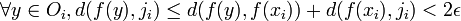
Montrons ensuite que B est complet. Il suffit pour cela de prouver que toute suite de Cauchy d'éléments fn de A converge dans C(K,F). Pour tout point x de K, la suite (fn(x)) est de Cauchy et à valeurs dans A(x), dont l'adhérence dans F est compacte donc complète, donc cette suite admet dans F une limite, f(x). Par équicontinuité, la convergence simple de (fn) vers f est uniforme sur le compact K.

















































