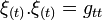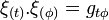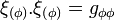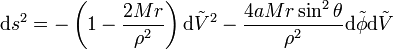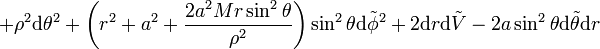Trou noir de Kerr - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En astrophysique, un trou noir de Kerr désigne un trou noir en rotation et de charge électrique nulle. Il est décrit dans le cadre de la relativité générale par la métrique de Kerr, qui ne dépend que de la masse M et du moment angulaire J.
Description
Contrairement au cas du trou noir sans rotation et sans charge électrique (appelé trou noir de Schwarzschild), le trou noir de Kerr possède une ergosphère en plus de son horizon des événements. Alors que ce dernier est décrit par une sphère de rayon rh, l'ergosphère est un ellipsoïde de révolution (oblate) dont le petit axe est aligné avec l'axe de rotation du trou noir et de même taille que rh, et le grand axe de taille rstat est situé dans le plan équatorial. De plus,
Horizon des événements
La présence de l'horizon des événements ne dépend pas de la rotation du trou noir, c'est une caractéristique commune à tous les types de trous noirs qui représente finalement l'essence même de ce qu'est un trou noir. Les particules qui franchissent l'horizon des événements tombent définitivement dans le trou noir sans possibilité de s'en échapper.
Dans le cas d'un trou noir de Kerr, le rayon de l'horizon des événements s'écrit :
-
![r_{h} = \frac{r_\mathrm{Sh}}{2} \left[ 1 + \sqrt{1-\left(\frac{Jc}{GM^2}\right)^2} \right]](https://static.techno-science.net/illustration/Definitions/autres/2/2c307b51bf69a34fbd9f3a8b1bf734f9_b5b4ea28858317cbd3b810016e68c53c.png)
où G est la constante gravitationnelle, c est la vitesse de la lumière, rSh est le rayon de Schwarzschild. La valeur du rayon de l'horizon du trou noir de Kerr est donc comprise entre la moitié du rayon de Schwarzschild (quand le moment angulaire est maximale, J = Mc) et ledit rayon (moment angulaire nul, J = 0, cas du trou noir de Schwarzschild).
Ergosphère
L'ergosphère est dite limite statique en ce sens que les particules qui la franchissent sont obligatoirement entraînées dans le sens de rotation du trou noir, autrement dit, elles y possèdent un moment angulaire de même signe que J. Cet entraînement confère du moment cinétique et de l'énergie mécanique à une particule qui pénètre dans l'ergosphère puis s'en échappe, de sorte que le trou noir voit son moment cinétique diminuer. C'est l'effet Penrose qui permet de pomper de l'énergie à un trou noir en rotation.
L'ergosphère est décrite par l'équation polaire :
où, toutes notations égales par ailleurs,θ désigne l'angle par rapport à l'axe de rotation. Il s'agit d'un ellipsoïde de révolution de petit axe rh et de grand axe rstat = rSh.
Métrique de Kerr
La métrique de Kerr s'écrit généralement dans les coordonnées de Boyer-Lindquist. En posant, G = c = 1, elle est donnée par :
-
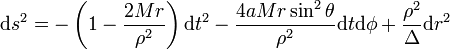
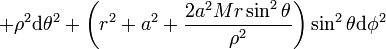
avec :
-
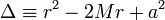
-
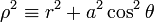
-
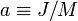
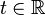
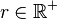
![\theta\in\left[0, \pi\right]](https://static.techno-science.net/illustration/Definitions/autres/2/25da40143820436475403a90f17b1634_0c99651d60ccf4b6323a082ef22a1c51.png)
![\phi\in\left[0, 2\pi\right]](https://static.techno-science.net/illustration/Definitions/autres/9/987aa223d64965c4d8e7ccbf2c6826b1_7f4e11cc8363a0250440a92935755ff0.png)
Les points θ = 0 et θ = π sont les pôles et les points
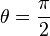
Le système de coordonnées est indéfinie aux pôles. En effet, lorsque t = cste et r = cste, le coefficient gφφ s'annule pour θ = 0 et θ = π.
De plus, les coordonnées sont invalides lorsque Δ = 0 où le coefficient grr diverge. Les coefficients de la métrique (exprimée dans les coordonnées de Boyer-Lindquist) sont indépendants de t et θ. Par conséquent, la géométrie de l'espace-temps est indépendante du temps (c'est-à-dire stationnaire) et à symétrie axiale.
Autrement dit, la métrique de Kerr possède les vecteurs de Killing :
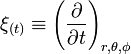
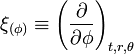
Les composantes de la métrique de Kerr exprimées avec les coordonnées de Boyer-Lindquist sont remarquables car elles sont égales au produit scalaire des coordonnées indépendantes :
Notons que si le moment angulaire par unité de masse est nul, a = 0 (donc J = 0), on obtient la métrique de Schwarzschild. Si on ajoute la contrainte, M = 0, on obtient l'espace de Minkowski.
Il arrive que la métrique soit exprimée dans les coordonnées de Kerr où
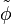
Dans ce cas, les coefficients sont indépendants de
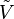
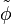
-
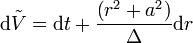
-
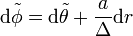
Il existe trois types différents d'espace-temps de Kerr suivant l'importance respective de M et a. Autrement dit, suivant la vitesse du moment angulaire J.
- L'espace-temps de Kerr lent (Slow Kerr space-time).
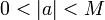
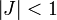
Δ possède alors deux racines réelles.
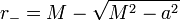
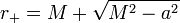
C'est la version de l'espace-temps de Kerr la plus souvent étudiée. L'espace-temps possède deux horizons, les sphères de rayon r = r − et r = r + diposées symétriquement à la sphère de rayon r = M. Le lieu géométrique où r = r + est appelé indifféremment l'horizon externe ou l'horizon des événements. Concernant r = r − , on le nomme horizon interne ou horizon de Cauchy. Les deux horizons séparent l'espace-temps en trois parties distinctes nommées Boyer-Lindquist Blocks:
- Block 1 :
 .
.
C'est la région extérieure au trou noir. L'ergosphère appartient à ce block. La limite statique est l'hypersurface définie par la racine supérieure de l'équation : ρ2 = 2Mr, où le coefficient gtt s'annule. Si on définit l'ergosphère par la coordonnée radiale r :
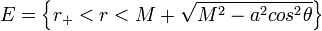
Cette équation permet de retrouver quelques résultats prévisibles :
La limite statique coïncide avec l'horizon des événements aux pôles.
L'extension radiale de l'ergosphère est maximum à l'équateur du trou noir (Voir Fig. 1).
La limite statique se rapproche de plus en plus de l'horizon des événements à mesure que le moment angulaire par unité de masse diminue.
Si un observateur franchit l'ergosphère, il lui est physiquement impossible de rester au repos par rapport à un objet extérieur au trou noir. De plus, tous les observateurs possédant une coordonnée radiale et un colatitude fixes se situant dans cette région de l'espace-temps de Kerr doivent décrire des orbites dans le même sens de rotation que le trou noir.
Si r = cste et θ = cste,  lorsque
lorsque
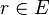
- Block 2 :
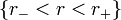
C'est la région située sous l'horizon externe. De la même manière que pour l'horizon de Schwarzschild caractérisant un trou noir sans rotation, aucun objet ne peut émerger de l'horizon des événements.
- Block 3 :
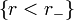
C'est la région de l'espace-temps située sous l'horizon interne contenant la singularité annulaire source de la gravité.
- L'espace-temps de Kerr extrême (Extreme Kerr space-time).
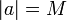
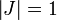
M est la racine double de Δ et la sphère de rayon r = M est l'horizon unique. Si on reprend les formules précédentes, on trouve que l'ergosphère est la région :
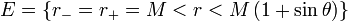
La métrique décrit un objet en rotation qui cesse d'être un trou noir, mais n'est pas à la vitesse de rupture. La vitesse de rotation du trou noir est égale à la vitesse de la lumière. Comme l'explique Jean-Pierre Luminet : "En language newtonien, on dirait qu'à la surface d'un trou noir maximal les forces de répulsion centrifuges compensent exactement les forces d'attraction gravitationnelles."
- L'espace-temps de Kerr rapide (Fast Kerr space-time).
 . La rotation est rapide (
. La rotation est rapide (  ).
).
Δ ne possède aucune racine réelle et l'espace-temps n'a pas d'horizon. Dans ce cas de figure, il n'y a pas de trou noir et on parle alors de singularité nue. L'intérêt de cette solution particulière est plutôt limité puisque Werner Israel a demontré dans les années 80 que toutes interactions d'un trou noir tournant à sa fréquence maximale (
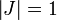
![r = \frac{r_\mathrm{S}}{2} \left[ 1 + \sqrt{1-\left(\frac{Jc}{GM^2}\cos\theta\right)^2} \right]](https://static.techno-science.net/illustration/Definitions/autres/a/a3a752e5a10e9d5fb98c8fdac1585c33_87645bafe45289f59ac5b0c1ca28a038.png)