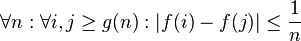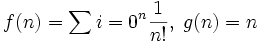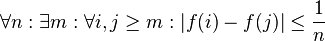Constructivisme (mathématiques) - Définition
Dans la philosophie des mathématiques, le constructivisme considère qu'il est nécessaire de trouver (ou "construire") un objet mathématique pour prouver qu'il existe. Selon les constructivistes, lorsqu'on suppose qu'un objet n'existe pas et on dérive une contradiction de cette hypothèse, l'objet n'a toujours pas été trouvé ni son existence prouvée. Voir preuve constructive.
Le constructivisme est souvent confondu avec l'intuitionnisme, mais en réalité, l'intuitionnisme n'est qu'une forme de constructivisme. L'intuitionnisme maintient que les fondations des mathématiques reposent sur l'intuition individuelle du mathématicien, faisant ainsi des mathématiques une activité intrinsèquement subjective. Au contraire, le constructivisme est en accord avec une vue objective des mathématiques.
Mathématiques constructives
Les mathématiques constructives utilisent une logique constructive, qui est essentiellement une logique classique où le principe du tiers exclu a été enlevé. Cela ne revient pas à dire que le principe du tiers exclu est complètement interdit; des cas particuliers de ce principe seront prouvables en tant que théorèmes. Simplement, le principe n'est pas supposé en tant qu'axiome (La loi de contradiction, en revanche, est toujours valide).
Par exemple, dans l'arithmétique de Heyting, il est possible de prouver que pour toute proposition p qui ne contient pas de quantificateur,
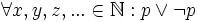
En fait, Luitzen Egbertus Jan Brouwer, le fondateur de l'école intuitionniste, voyait le principe du tiers exclu comme quelque chose qui était extrait de l'expérience du fini, et qui était appliqué par les mathématiciens à l'infini, sans justification. Par exemple, la conjecture de Goldbach est l'hypothèse que tout nombre pair (plus grand que 2) est la somme de deux nombres premiers. Il est possible de tester pour chaque nombre pair particulier s'il est ou non la somme de deux nombres premiers (par exemple avec une recherche exhaustive), alors il est juste de dire que chacun d'entre eux est ou bien la somme de nombres premiers, ou ne l'est pas. Et ainsi de suite, chacun d'entre eux testé jusqu'à présent est bien la somme de deux nombres premiers.
Cependant, il n'y a aucune preuve connue que la propriété est vraie pour tout nombre pair, ni aucune preuve du contraire. Ainsi, pour Brouwer, il n'est pas possible de dire "ou bien la conjecture de Goldbach est vraie, ou elle ne l'est pas". Et indépendamment du fait que la conjecture puisse être un jour prouvée, l'argument s'applique aux problèmes similaires non résolus. Pour Brouwer, le principe du tiers exclu était équivalent à supposer que chaque problème mathématique possède une solution.
En se séparant du principe du tiers exclu en tant qu'axiome, la logique constructiviste possède une propriété d'existence que la logique classique n'a pas : lorsque
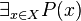
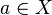
Exemple en analyse réelle
En analyse réelle classique, une manière de définir un nombre réel est de l'identifier à une classe de suites de Cauchy de nombres rationnels.
En mathématiques constructives, une manière de construire un nombre réel est en tant qu'une fonction f prenant un entier positif n et rendant un rationnel f(n), en même temps qu'une fonction g prenant un entier positif n et rendant un entier positif g(n) tel que
de telle sorte qu'alors la valeur n augmente, les valeurs de f(n) se rapprochent de plus en plus. On peut alors utiliser f et g ensemble pour calculer aussi précisément que souhaité une approximation rationnelle du nombre réel qu'elles représentent.
Avec cette définition, une représentation simple du nombre réel e est :
Cette définition correspond à la définition classique en utilisant les suites de Cauchy, mais avec une touche constructive : pour une suite de Cauchy classique, il est requis que pour toute distance préalablement donnée, aussi petite soit-elle, il existe (au sens classique) un terme de la suite après lequel tous les termes sont plus proches que la distance donnée. Dans la version constructive, il est requis que pour chaque distance donnée, il soit dans les faits possible de spécifier un point de la suite où cela se produit. En fait, l'interprétation constructive standard de l'énoncé mathématique
est précisément l'existence de la fonction calculant le module de convergence. Ainsi la différence entre les deux définitions des nombres réels peut être vue comme la différence dans l'interprétation de l'énoncé "pour tout ... il existe".
Cela pose la question de savoir quelle sorte de fonction d'un ensemble dénombrable vers un ensemble dénombrable, telle que f et g ci-dessus, peut en réalité être construite. Différentes versions du constructivisme divergent sur ce point. Les constructions peuvent être définies aussi généralement comme des séquences de choix libre, ce qui est le point de vue intuitionniste, ou aussi étroitement comme des algorithmes (ou plus précisément des fonctions récursives), ou même laissées non spécifiées. Si par exemple le point de vue algorithmique est pris, alors les réels construits ici sont essentiellement ce que serait appelé de manière classique les nombres réels calculables.
Cardinalité
Prendre l'interprétation algorithmique ci-dessus peut paraître étrange avec les notions classiques de cardinalité. En énumérant les algorithmes, il est possible de montrer classiquement que les nombres calculables sont dénombrables. Et cependant, l'argument de la diagonale de Cantor montre que les nombres réels ont une plus grande cardinalité. De plus, l'argument de la diagonale semble parfaitement constructif. Identifier les nombres réels avec les nombres calculables serait alors une contradiction.
Et dans les faits, l'argument de la diagonale de Cantor est constructif, au sens où étant donnée une bijection entre les nombres réels et les nombres naturels, on construit un nombre réel qui ne correspond pas, et prouve ainsi une contradiction. On peut en effet énumérer les algorithmes pour construire une fonction T des entiers naturels vers les réels. Mais, à chaque algorithme, il peut ou non correspondre un nombre réel, puisque que l'algorithme peut échouer à satisfaire les contraintes, ou même ne pas terminer (T est une fonction partielle), et cela fait échouer la production de la bijection requise.
Cependant, on pourrait espérer que puisque T est une fonction partielle des entiers naturels vers les nombres réels, les nombres réels ne sont pas plus que dénombrables. Et, puisque chaque nombre entier peut être trivialement représenté par un nombre réel, alors les nombres réels ne sont pas moins que dénombrables. Ils sont donc exactement dénombrables. Cependant, ce raisonnement n'est pas constructif, puisqu'il ne construit pas dans les faits la bijection requise. En fait, la cardinalité des ensembles n'est pas totalement ordonné (voir le théorème de Cantor-Bernstein).
Attitude des mathématiciens
Traditionnellement, les mathématiciens ont été très suspicieux, si ce n'est complètement opposés, envers les mathématiques constructives, largement en raison des limitations que cela pose pour l'analyse constructive. Ces positions ont été exprimées avec force par David Hilbert en 1928, quand il écrit dans Die Grundlagen der Mathematik, "Enlever le principe du tiers exclu aux mathématiciens serait la même chose, disons, que d'interdire le télescope aux astronomes ou aux boxeurs l'usage des poings" (lien) Errett Bishop, dans son ouvrage de 1967 Foundations of Constructive Analysis, a travaillé pour dissiper ces craintes en développant un grand morceau de l'analyse traditionnelle dans un cadre constructif. Cependant, tous les mathématiciens n'admettent pas que Bishop ait réussi, puisque son livre est nécessairement plus compliqué qu'un livre d'analyse classique le serait. Dans tous les cas, la plupart des mathématiciens n'ont pas besoin de se restreindre à des méthodes constructives, même si cela peut être fait.
(lien) Traduction de Stanford Encyclopedia of Philosophy, http://plato.stanford.edu/entries/mathematics-constructive/.
Mathématiciens ayant contribué au constructivisme
- Errett Bishop
- Paul Lorenzen
- Leopold Kronecker (constructivisme)
- L.E.J. Brouwer (intuitionnisme)
- Arend Heyting (logique intuitionniste)
Branches
- Logique constructive
- Théorie des types constructives
- Analyse constructive