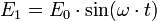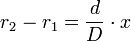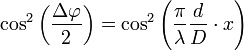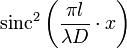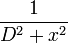Fentes de Young - Définition
Les fentes de Young sont l'objet d'une expérience de physique réalisée en 1801 par Thomas Young qui consiste à diriger de la lumière sur deux petit trous (ou fentes). La lumière est ensuite récupérée sur un écran. On y observe un motif de diffraction, c'est-à-dire que certains endroits sur l'écran sont totalement sombres, et d'autres sont très lumineux, du fait de l'interférence des rayons diffusés par les deux fentes.
Cette expérience permet alors de mettre en évidence la nature ondulatoire de la lumière. Elle a été également réalisée avec de la matière, comme les électrons, neutrons, atomes, molécules, avec lesquels on observe aussi des interférences. Cela illustre la dualité onde-particule : les interférences montrent que la matière présente un comportement ondulatoire, mais la façon dont ils sont détectés (impact sur un écran) montre leur comportement particulaire.
Des expérience similaires aux fentes de Young impliquant des électrons ont été réalisées. En 1961, Claus Jönsson à Tübingen produisait des interférences avec un fil d'araignée métallisé séparant un faisceau d'électrons en deux. En 1989, Tonomura et al. ont envoyé un électron sur un biprisme à électrons. Ils ont observé la figure d'interférence prédite par la théorie.
Interprétation classique du phénomène
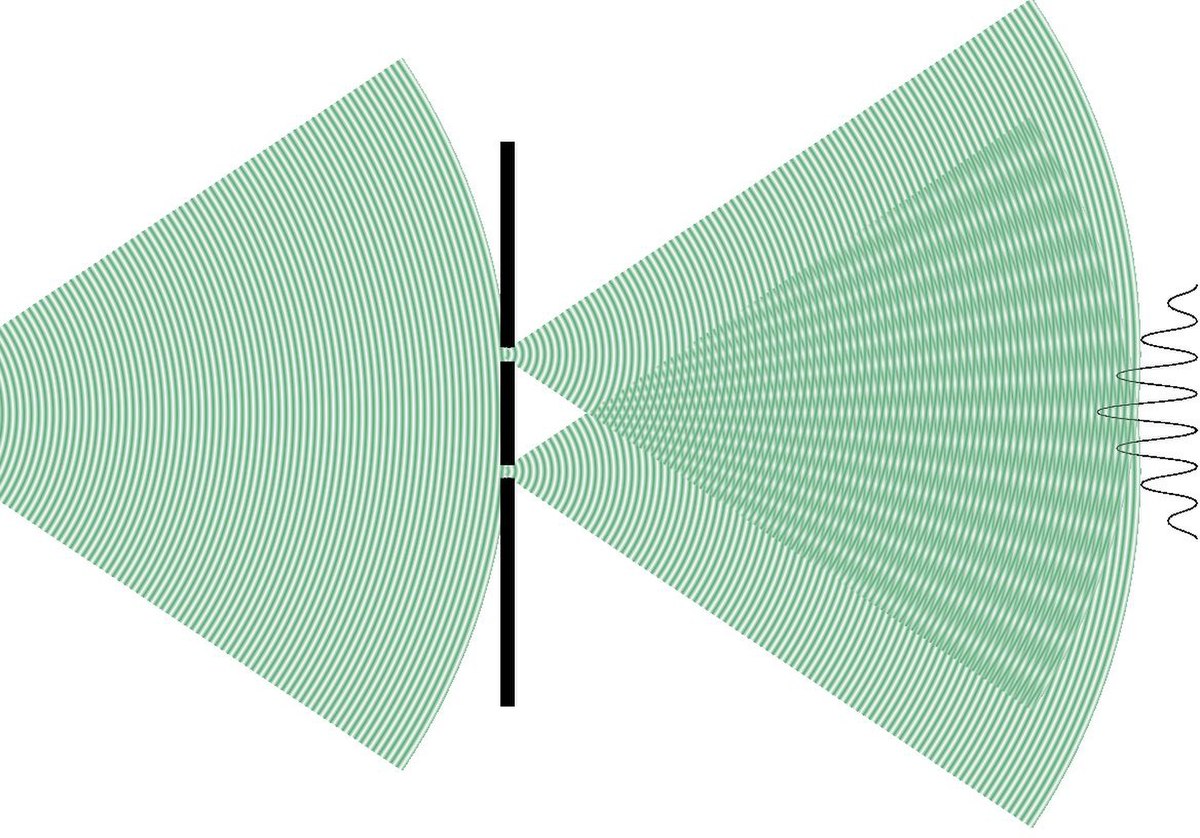
Dans l'expérience de Young, on utilise une source lumineuse S monochromatique[1] et on interpose une plaque percée de 2 fentes. Celles-ci se comportent comme des sources secondaires S1 et S2. On observe alors, sur un écran placé derrière, des franges alternativement sombres et claires : les ondes issues de S1 et S2 interfèrent entre elles.
Considérons maintenant un point M situé sur l'écran. Il est éclairé par les ondes lumineuses émises par S1 et S2 qui peuvent s'écrire respectivement, au point M :
et
-
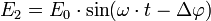
où E0 est l'amplitude[2], ω la pulsation des ondes, Δφ leur déphasage et t le temps.
Δφ caractérise le fait qu'une onde a un certain retard par rapport à l'autre. En effet, pour arriver au point M, le chemin à parcourir n'est pas de la même longueur pour la lumière qui provient d'une source ou de l'autre.
Si Δφ est un multiple de 2π, les ondes s'ajoutent et on obtient une frange lumineuse sur l'écran, ce que l'on appelle une interférence constructive. En revanche si Δφ est un multiple impair de π alors les ondes s'annulent et on obtient une frange sombre sur l'écran, c'est alors une interférence destructive. Cela explique pourquoi on observe, sur l'écran, des franges successivement claires et sombres. Mais il n'y a pas, a priori, de formule simple permettant de décrire ces franges. Pour simplifier le problème, il est possible de supposer que l'écran est placé loin des fentes.
Cas d'un écran éloigné
Supposer que l'écran est éloigné des fentes revient, plus précisément, à poser que la distance D entre l'écran et les fentes est grande devant la distance d entre les fentes (c'est-à-direD ? d).
Cette approximation est utile dans le calcul de Δφ. En effet, les distances de M à S1 et de M à S2, notées respectivement r1 et r2, vérifient alors :
où x est la distance de M au centre de l'écran.
Cette différence de trajet, souvent appelée différence de marche, correspond à un déphasage entre les deux rayons :
-
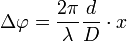
On peut alors montrer que l'intensité reçue au niveau de l'écran est proportionnelle à :
L'intensité est donc répartie de manière périodique : les franges sont séparées d'une distance D⋅λ/d. Cela correspond, pour une lumière visible, avec des fentes séparées d'un millimètre, à des franges séparées d'un millimètre sur un écran placé à deux mètres.
Cas d'un écran à l'infini
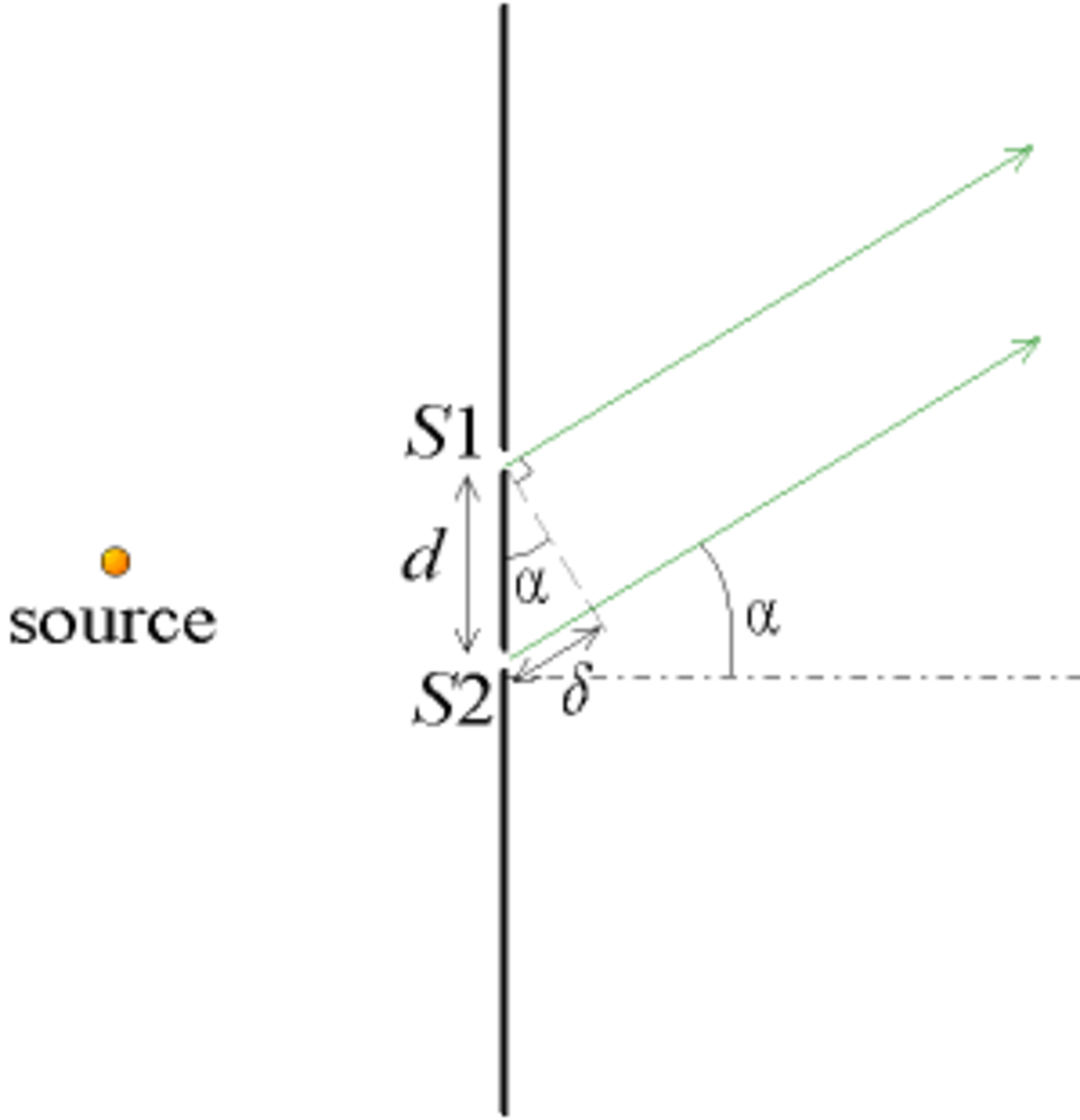
Pour pousser l'approximation à sa limite, on peut étudier le cas où les rayons interfèrent à l'infini, c'est-à-dire lorsqu'ils sont parallèles entre eux. Dans la pratique, cela s'obtient en plaçant l'écran à plusieurs mètres des fentes, ou bien en plaçant l'écran au foyer image d'une lentille convergente.
Dans ce cas, on montre rapidement (voir la figure ci-contre) que la différence de marche entre deux rayons interférant entre eux vaut :
-
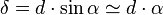
Le même raisonnement que la dans la partie précédente donne un angle entre les franges valant λ/d.
Ces résultats aboutissent aux observations suivantes :
- plus les fentes sont éloignées l'une de l'autre, plus les franges sont rapprochées ;
- plus l'écran est éloigné, plus les franges sont espacées.
Rôle de la diffraction par chaque fente
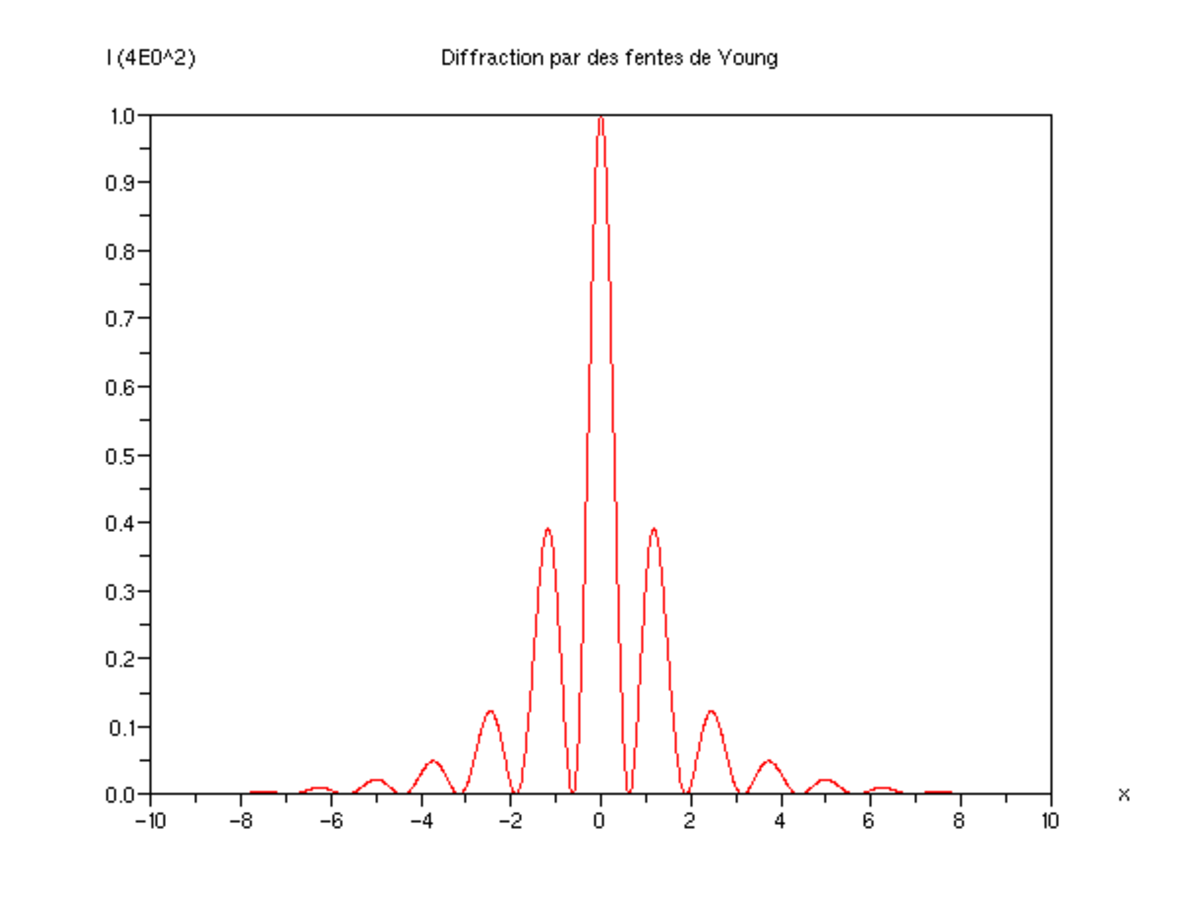
Les calculs précédents montrent que l'intensité des franges est partout égale. Or on observe (voir figure ci-contre) que leur intensité diminue lorsqu'on s'éloigne du centre de l'écran. Deux phénomènes sont à l'origine de cette observation.
Premièrement, les fentes ont une certaine largeur, ce qui implique un phénomène de diffraction par chacune des fentes. En effet, une lumière envoyée sur un petit trou n'en ressort pas de façon isotrope (on observe une tache d'Airy). Cela se traduit par le fait que la lumière est majoritairement dirigée vers l'avant. Cet effet se répercute sur la figure observée après les fentes d'Young : l'intensité des franges décroît au fur et à mesure que l'on s'éloigne du centre. Pour en tenir compte, il faut rajouter le facteur suivant à l'intensité reçue par l'écran :
où sinc est la fonction sinus cardinal et l est la largeur de chaque fente.
Le second phénomène à prendre en compte est le fait que les ondes émises en S1 et S2 sont des ondes spériques, c'est-à-dire que leur amplitude décroît au fur-et-à-mesure qu'elles avancent. Ainsi l'amplitude de E1 et de E2 ne sera pas la même au point M. Cela donne un nouveau facteur à rajouter à l'intensité :
On a donc au final
-
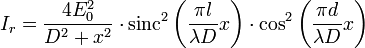
Interprétation quantique du phénomène
L'expérience originelle de Thomas Young pouvait être interprétée de manière " classique " (voir ci-dessus), en utilisant les simples lois de Fresnel, et mettait en évidence le caractère ondulatoire de la lumière.
L'expérience de Young a par la suite été raffinée, notamment faisant en sorte que la source S émette un quantum à la fois. Par exemple, on peut à l'heure actuelle émettre des photons ou des électrons un par un. Ceux-ci sont détectés un par un sur l'écran placé après les fentes d'Young : on observe alors que ces impacts forment petit à petit la figure d'interférences. Selon des lois classiques concernant les trajectoires de ces corpuscules, il est impossible d'interpréter ce phénomène.
L'interprétation quantique du phénomène est la suivante : le quantum émis prend un état superposé lors du franchissement de la plaque : |quantum passe par S1> + |quantum passe par S2> (voir Notation bra-ket). De la fonction d'onde résultante, on peut déterminer pour chaque point de la plaque la probabilité que le quantum y soit détecté. On peut démontrer que la distribution des probabilités suit la figure d'interférence. Autrement dit, le quantum passerait par les deux fentes à la fois, et interfèrerait avec lui-même.
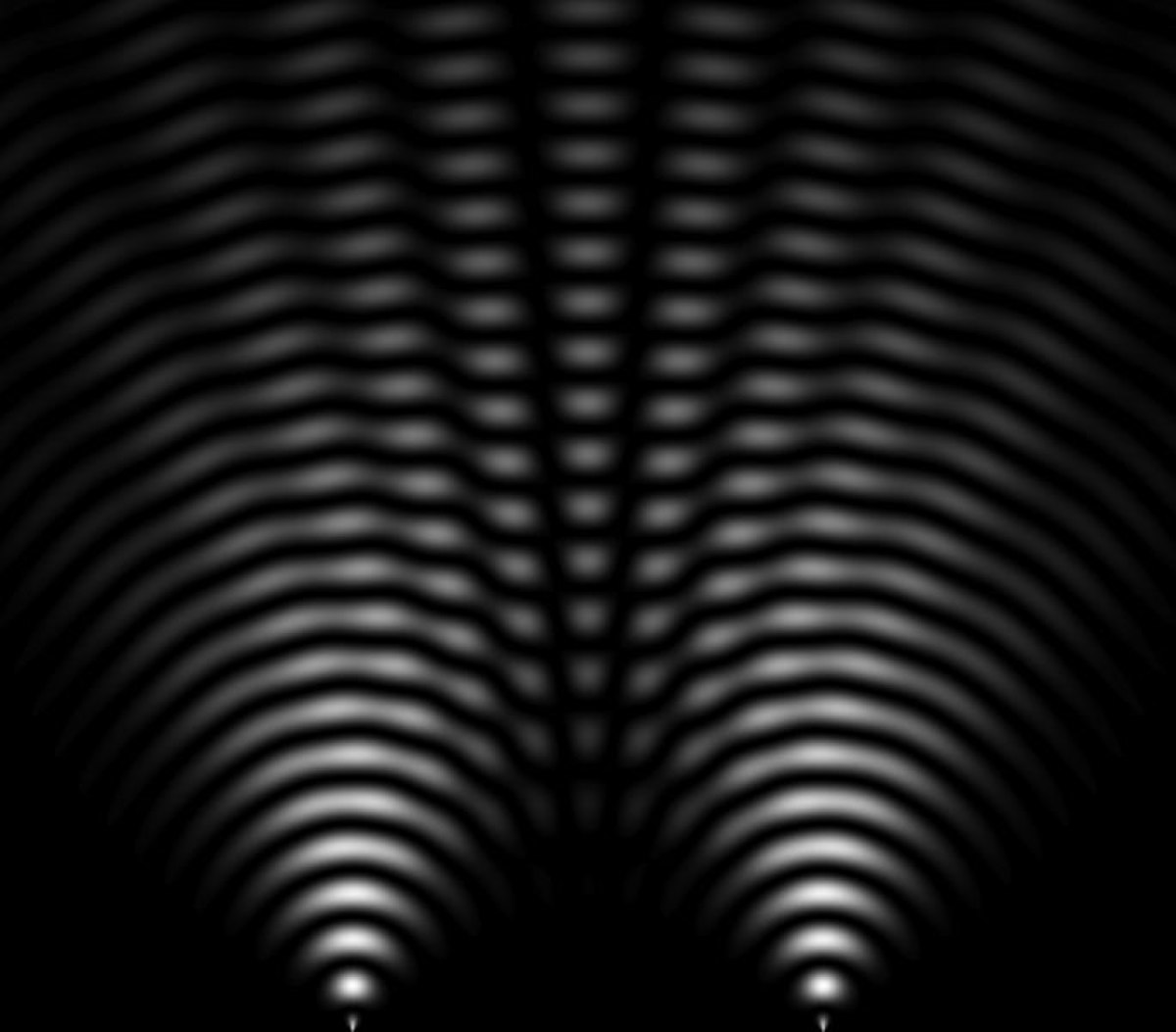
La figure ci-contre montre l'évolution de la fonction d'onde d'un électron au passage des deux fentes. Les niveaux de gris représentent la densité de probabilité de présence de l'électron. La taille réelle de l'électron est en fait bien plus petite que sa zone de probabilité de présence (en forme de cercle) initiale. On voit nettement que l'électron "interfère avec lui-même": les franges d'interférences sont bien visibles au sortir des deux fentes (l'électron possède aussi une certaine probabilité de "rebondir" et de former également une figure d'interférence vers l'arrière).
Destruction de la figure d'interférence. Problème de la mesure
L'interprétation quantique de l'expérience repose sur le fait qu'un photon individuel se retrouve dans un état superposé suite au franchissement des fentes. On peut interpréter ce fait en disant que le photon est passé par les deux fentes en même temps. Mais que se passe-t-il si, insatisfait par cette interprétation des choses, on cherche à détecter par quelle fente le photon "est réellement passé" ?
Le résultat net de l'expérience est qu'on détecte bien que le photon passe soit dans la fente de droite, soit dans la fente de gauche, mais alors la figure d'interférence disparait : le photon n'est plus dans un état superposé suite à la mesure. La détection du photon dans l'une des fentes provoque un "effondrement de la fonction d'onde" et de l'état superposé. Autrement dit, toute tentative de savoir de quel côté le quantum est passé ne permet plus d'obtenir des interférences.
L'expérience de Young permet donc également de mettre en évidence le problème de la mesure quantique. Ce problème est que les lois quantiques ne prévoient pas directement cet effondrement, et qu'il n'existe donc pas de définition objective et rigoureuse de ce qu'est une "mesure" (voir traitement complet de ce problème dans les articles Chat de Schrödinger et Problème de la mesure quantique).
A l'heure actuelle, des développements sur le sujet permettent de réaliser des expériences très similaires sur des objets de plus en plus volumineux, comme les atomes, les molécules, les condensats de Bose-Einstein. En particulier, on a observé des interférences avec des molécules de fullerène. Ces expériences démontrent que la vision purement corpusculaire de la matière n'est pas satisfaisante avec des objets de plus en plus gros, d'où la question récurrente de la dualité onde-corpuscule en physique quantique.