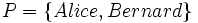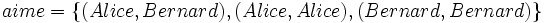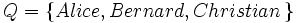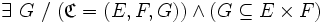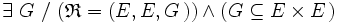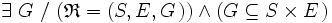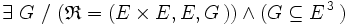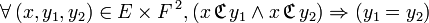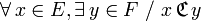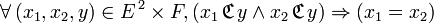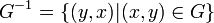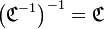Correspondance et relation - Définition
En algèbre générale, la notion de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison.
De manière informelle, une relation dans un ensemble ( on dit aussi " sur un ensemble " ) est une proposition qui lie un certain nombre d’éléments. Sur un ensemble constitué de personnes, par exemple, on pourrait définir une relation " Alice aime Bernard ", ou " Cecile connaît David "... On peut donc voir une relation comme des fils reliant divers éléments d’un ensemble.
Cette notion peut être généralisée en établissant des liens entre des éléments d’ensembles distincts.
Graphe et correspondance
Le lien entre deux éléments peut s’exprimer de manière plus formelle par un " couple ". Un couple, noté entre parenthèses, est constitué de deux éléments mis dans un ordre particulier. Les correspondances, ou relations générales peuvent ainsi être considérées en première approche comme des ensembles de couples, c’est-à-dire des graphes. Mais cela ne suffit pas toujours :
- Les propriétés des correspondances dépendent autant des absences de liens entre éléments que de leur existence.
En d’autres termes, la donnée du graphe d’une correspondance ne suffit pas à définir complètement celle-ci ; il faut aussi savoir quels sont les couples d'éléments qu'elle ne lie pas. Cela revient à préciser dans quel produit cartésien s’inscrit la correspondance.
Néanmoins, il demeure possible, le plus souvent, de confondre une correspondance avec son graphe, du moment qu’il n’y a pas d’ambiguïté sur le produit cartésien dans lequel elle s’inscrit.
Pour illustrer ces idées, considérons par exemple l’ensemble P suivant de personnes :
Définissons-y naïvement la relation aime par la seule donnée de son graphe :
Pour la relation aime, si " Alice aime Bernard ", alors le couple ( Alice, Bernard ) fait partie de l’ensemble aime.
L’ensemble aime est un sous-ensemble de P × P. Nous constatons que :
- la relation aime est une relation binaire dans P ;
- la relation aime est réflexive, puisque toutes les personnes considérées s’aiment elles-mêmes.
Remarquons au passage que l’ordre dans le couple a de l’importance. Si " Alice aime Bernard ", la réciproque n’est pas forcément vraie, et d’ailleurs ici ( Bernard , Alice ) n’appartient pas à aime.
Ajoutons une personne à P. L’ensemble des personnes devient :
aime est encore un sous-ensemble de Q × Q, mais la relation aime n’est plus réflexive : la simple présence de Christian a modifié la relation, même si aucun lien n’a été rajouté.
En fait, la relation aime dans Q doit être distinguée de la relation aime dans P, même si elles ont toutes deux le même graphe. Pour y parvenir, l’idée la plus simple est de considérer qu’une relation comporte non seulement un graphe, mais aussi le produit cartésien dans lequel il s’inscrit : si aime désigne toujours le graphe, les relations deviennent alors :
-
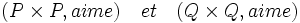
ou, ce qui revient en pratique au même :
-
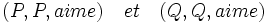
Cette façon de procéder comporte toutefois encore un défaut : elle ne permet pas de généraliser les relations aux classes propres, puisque les éléments de n-uplets doivent être des ensembles. Cela pose problème avec la relation d’équipotence par exemple, qui est à la base de la définition des cardinaux, et qui est censée être définie dans la classe de tous les ensembles.
Une solution (déjà entrevue dans l’article " Produit cartésien ") consiste à remplacer les triplets précédents par des sommes disjointes : les deux relations précédentes seront alors définies comme :
-
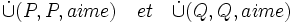
mais encore notées cependant par abus d’écriture :
-
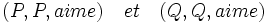
- Remarque
- Le cheminement ci-dessus est caractéristique de la démarche des mathématiciens lorsqu’ils élaborent une définition : ils partent d’une première approche simple, qu’ils améliorent ensuite en la compliquant pour éliminer des contradictions internes ou prendre en compte certains cas particuliers, puis qu’ils généralisent au maximum.
Définition formelle
Notes préliminaires
- Pour alléger l’écriture, nous noterons à partir d’ici les sommes disjointes comme des n-uplets.
- Les définitions suivantes demeurent ainsi valides si on y remplace les ensembles par des classes même propres.
Définition
- Une correspondance, ou relation générale, est la somme disjointe de trois ensembles dont le dernier est une partie du produit cartésien du premier par le deuxième.
Plus précisément, si E et F sont deux ensembles, alors
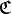
E est l’ensemble de départ de la correspondance, F son ensemble d’arrivée et G son graphe.
En pratique, on confondra une correspondance avec son graphe s’il n’y a pas d’ambiguïté sur les ensembles de départ et d’arrivée.
Égalité de deux correspondances
D’après leur définition, deux correspondances sont égales si et seulement si elles ont mêmes ensembles de départ et d’arrivée et même graphe.
En d’autres termes, si
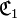
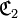
-
![( \mathfrak{C}_1 = \mathfrak{C}_2 ) \Leftrightarrow [ ( E_1 = E_2 ) \wedge ( F_1 = F_2 ) \wedge ( G_1 = G_2 ) ] \,](https://static.techno-science.net/illustration/Definitions/autres/d/d970beed51e39f940d4585f94d443a6b_3eb57bcf67b32ebbe46453e349fc9699.png)
Exemples et cas particuliers importants
- Etudier quels sont les sports pratiqués par les français revient à établir une correspondance de l'ensemble des français dans l'ensemble des sports possibles.
- Si E = { a, b, c, d } , F = { 1, 2, 3 } et si G = { ( a, 1 ), ( b, 2), ( b, 3), (c, 3) }, alors ( E, F, G ) est une correspondance de E dans F.
- Une correspondance est vide si et seulement si son graphe est égal à l'ensemble vide.
- Une correspondance est pleine si et seulement si son graphe est égal au produit cartésien des ensembles de départ et d'arrivée tout entier.
- La relation dans E dont le graphe est la diagonale de E est appelée identité de E, et notée habituellement "
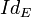
- L'ensemble de départ d'une correspondance peut être le produit cartésien de deux ensembles ou plus : ainsi, l'addition des nombres réels est une correspondance de

Représentation des correspondances
Il existe trois types de représentation d’une correspondance :
- sagittale, qui dérive des diagrammes de Venn pour les ensembles, où les ensembles de départ et d’arrivée sont représentés par deux " patatoïdes " côte à côte, les éléments par des points à l’intérieur des patatoïdes, et les couples du graphe par des flèches reliant les premières composantes aux secondes ;
- tabulaire ou matricielle, sous forme d’un tableau à deux entrées, avec en première colonne la liste des éléments de l’ensemble de départ et en première ligne celle des éléments de l’ensemble d’arrivée. Les couples sont représentés par des croix dans les cases à l’intersection de la ligne de la première composante et de la colonne de la seconde composante ;
| . | Bernard | Antoine | Paul | Charles |
|---|---|---|---|---|
| Lucie | X | X | X | . |
| Béatrice | . | X | . | . |
| Delphine | . | . | . | . |
| Alice | X | . | X | . |
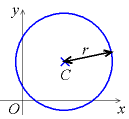
- graphique, avec un axe horizontal dont les points représentent les éléments de l’ensemble de départ, et un axe vertical dont les points représentent les éléments de l’ensemble d’arrivée. Les couples sont représentés par les points à l’intersection de la ligne verticale coupant l’axe horizontal à l’emplacement de la première composante, et de la ligne horizontale coupant l’axe vertical à l’emplacement de la seconde composante. Traditionnellement, le nuage des points du graphe se situe au-dessus et à droite des axes.
Relations n-aires
Relations internes et externes
Une relation interne ou relation dans un ensemble ou relation sur un ensemble est une correspondance dont l’ensemble de départ est une puissance cartésienne de l’ensemble d’arrivée.
Une relation externe est une correspondance dont l’ensemble de départ est le produit cartésien d’un ensemble dit de scalaires ou d’opérateurs par une puissance cartésienne de l’ensemble d’arrivée.
Plus précisément, si E et S sont deux ensembles :
- -

-
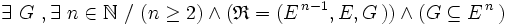
- -

-
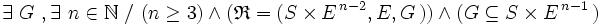
- -

-
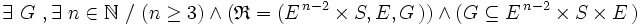
Pour que ces définitions soient cohérentes, S ne doit pas être un produit cartésien où E figure ( le cas S = E est toutefois toléré par abus de langage : une relation interne est alors vue comme une relation externe dans E à opérateurs dans E lui-même ).
Les correspondances de S dans E où S n'est ni E, ni un produit cartésien comportant E ne relèvent pas de ces définitions, mais peuvent être vues comme relations externes dans E au cas limite où n = 2. S est alors l'ensemble des opérateurs ( sans préciser à gauche ou à droite, les deux se confondant ).
A part ce cas, s’il n’est pas précisé si une relation externe est à gauche ou à droite, et si le contexte ne permet pas de lever l’ambiguïté, alors elle est à gauche. De même, s’il n’est pas précisé si une relation est interne, externe ou générale, et si le contexte ne permet pas de lever l’ambiguïté, alors elle est interne. Pour parler des relations au sens général du terme, il vaudra mieux préciser relation générale, ou employer le terme de correspondance.
Arité d’une relation
Le nombre n intervenant dans les définitions précédentes est appelé arité de la relation. Celle-ci est dite n-aire; ainsi :
- une relation binaire interne, d’arité 2 , est une correspondance dont les ensembles de départ et d’arrivée sont les mêmes. En d’autres termes, si E est un ensemble,

- une relation binaire externe, encore d'arité 2, est une correspondance d’un ensemble S dans un ensemble E, où S n’est pas un produit cartésien dont E soit une composante; en d’autres termes, si E et S sont deux ensembles,

- une relation ternaire interne, d'arité 3, est une correspondance dont l’ensemble de départ est le carré cartésien de l’ensemble d’arrivée; en d’autres termes, si E est un ensemble,

- une relation ternaire externe à gauche (resp. à droite) est une correspondance dont l’ensemble de départ est le produit cartésien d’un ensemble S de scalaires par l’ensemble d’arrivée (resp. de l'ensemble d'arrivée par un ensemble S de scalaires); en d’autres termes, si E et S sont deux ensembles :,

- - à gauche ssi :
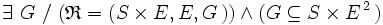
- - à droite ssi :
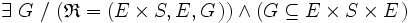
Encore une fois, l’ensemble S ci-dessus ne doit pas être un produit cartésien dont l’ensemble d’arrivée E soit une composante.
En pratique, on considère rarement des relations d'arité supérieure, car elles peuvent toujours se décomposer en relations binaires ou ternaires.
Exemples
- L’égalité et l’inclusion sont des relations binaires dans l’univers des ensembles.
- La réunion, l’intersection, la différence et la différence symétrique sont des relations ternaires internes dans l’univers des ensembles.
- Si A, B et C sont trois ensembles disjoints deux à deux :
-
- toute relation de A dans A est binaire interne ;
- toute relation de A dans B est binaire externe ;
- toute relation de A x A dans A est ternaire interne ;
- toute relation de A x A dans B est scalaire ( voir paragraphe suivant ) ;
- toute relation de A x B dans A est ternaire externe à droite ;
- toute relation de A x B dans B est ternaire externe à gauche ;
- et enfin, toute relation de A x B dans C est binaire externe ( pour l'arité, la référence est l'ensemble d'arrivée ! ) ;
Relations scalaires
Une relation scalaire est une correspondance d'un ensemble E 2 dans un ensemble S, où S n'est pas un produit cartésien dont l’ensemble E soit une composante ; c'est donc une relation binaire externe dont l'ensemble de départ est un carré cartésien.
L'appellation de relation scalaire peut être étendue au cas où l'ensemble de départ n'est pas un carré cartésien, mais une puissance cartésienne d'ordre n supérieur à 2. La valeur n+1 est parfois appelée arité scalaire de la relation, à ne pas confondre avec l'arité définie précédemment (toujours égale à 2 pour une relation scalaire).
Fonctions
Images et antécédents
Si
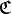
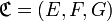
- - y correspond à x par
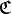
- - ( x , y ) appartient à G ;
- - y est image de x par
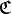
- - x est antécédent de y par
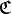
Le terme de " préimage " est parfois employé à la place de celui d'" antécédent ".
" y correspond à x par
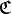
- " ( x , y ) ∈ G(
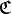
- " ( x , y )
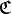
- "
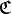
- " x
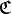
Cette dernière notation est, sauf cas particulier, la plus pratique et par conséquent la plus utilisée.
L'ensemble formé par les images de tous les éléments de l’ensemble de départ d’une correspondance est appelé ensemble-image de cette correspondance. Il est noté habituellement "
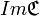
Symétriquement, l’ensemble formé par les antécédents de tous les éléments de l’ensemble d’arrivée d’une correspondance est appelé ensemble-antécédent de cette correspondance. Il est noté habituellement "
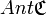
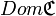
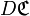
Fonctions, applications et bijections
Propriétés de base
Une correspondance peut avoir quatre propriétés de base indépendantes les unes des autres. Elle peut être :
- fonctionnelle : tout élément de l'ensemble de départ a au plus une image :
- applicative : tout élément de l'ensemble de départ a au moins une image :
- injective : tout élément de l'ensemble d'arrivée a au plus un antécédent :
- surjective : tout élément de l'ensemble d'arrivée a au moins un antécédent :
-
-
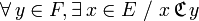
-
- Définitions équivalentes
- Une correspondance est applicative si et seulement si son ensemble-antécédent se confond avec son ensemble de départ, c'est-à-dire si :
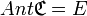
- Une correspondance est surjective si et seulement si son ensemble-image se confond avec son ensemble d'arrivée, c'est-à-dire si :
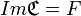
Définitions
En combinant ces quatre propriétés de base, nous obtenons a priori 16 types de correspondances, mais seules 9 ont un qualificatif. Il est possible de résumer ces propriétés et leur définition dans le tableau suivant :
| Propriété : | au plus ... | au moins ... | exactement ... | ... |
| Correspondance : | fonctionnelle | applicative | univoque | ... une image par élément de l'ensemble de départ |
|---|---|---|---|---|
| injective | surjective | bijective | ... un antécédent par élément de l'ensemble d'arrivée | |
| bifonctionnelle | biapplicative | biunivoque | ... une image par élément de départ et un antécédent par élément d'arrivée |
Certaines des combinaisons des quatre propriétés de base ont reçu un nom, en raison de leur importance pratique :
- Une fonction est une correspondance fonctionnelle. Chaque élément de départ a au plus une image. On peut donc parler de son image sans ambiguïté, et la désigner par un symbole, d'habitude " R( x ) " si la fonction est notée " R ". Cela permet de remplacer la notation relationnelle " x R y " par la notation fonctionnelle " y = R( x ) " plus pratique ;
- Une application est une fonction applicative. C’est donc aussi une correspondance fonctionnelle et applicative, c’est-à-dire une correspondance univoque. Comme elle est applicative, son domaine de définition se confond avec son ensemble de départ ;
- Une injection est une application injective. C’est donc une correspondance fonctionnelle, applicative et injective, c’est-à-dire une correspondance applicative et bifonctionnelle ;
- Une surjection est une application surjective. C’est donc une correspondance fonctionnelle, applicative et surjective, c’est-à-dire une fonction biapplicative. Comme elle est surjective, son image n'est autre que l'ensemble d'arrivée tout entier ;
- Une bijection est une application bijective. C’est donc une correspondance fonctionnelle, applicative, injective et surjective, c’est-à-dire une correspondance biunivoque.
- Attention !
- Une correspondance applicative (respectivement injective, surjective, bijective) n’est pas en général une application (respectivement une injection, une surjection, une bijection).
- De même, une fonction injective (respectivement surjective, bijective) n’est pas en général une injection (respectivement une surjection, une bijection).
Correspondance réciproque
Les notions d’image et d’antécédent sont duales. Échanger leur rôle revient à échanger entre elles les composantes de chaque couple du graphe, donc à remplacer chaque couple ( x , y ) par son couple réciproque ( y , x ).
Le graphe réciproque d’un graphe G, noté " G − 1 ", est le graphe résultant d’un tel échange :
La correspondance réciproque d’une correspondance est la correspondance obtenue en échangeant les ensembles de départ et d’arrivée et en remplaçant le graphe par son graphe réciproque.
En d’autres termes, si
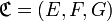
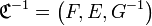
La réciproque de la réciproque d’une correspondance n’est autre que cette correspondance :
Il suffit de lire le tableau des combinaisons des propriétés de base des correspondances (voir plus haut), en échangeant le rôle des images et des antécédents, pour obtenir les propriétés des réciproques. Ainsi :
- La réciproque d’une fonction est une correspondance injective. Inversement, pour que la réciproque d’une correspondance soit une fonction, il faut et il suffit que cette correspondance soit injective ;
- La réciproque d’une correspondance applicative est surjective, et vice-versa ;
- La réciproque d’une application, c'est-à-dire d'une correspondance univoque, est une correspondance bijective. Inversement, pour que la réciproque d’une correspondance soit une application, il faut et il suffit que cette correspondance soit bijective ;
- La réciproque d'une correspondance bifonctionnelle, c’est-à-dire d’une fonction injective, est une correspondance bifonctionnelle, c’est-à-dire une fonction injective ;
- La réciproque d’une correspondance biapplicative est elle-même biapplicative ;
- Enfin, la réciproque d’une bijection, c'est-à-dire d'une correspondance biunivoque, est une bijection.
Classement des correspondances
| Correspondances | Relations binaires internes | Relations ternaires internes | Relations ternaires externes (*) |
|---|---|---|---|
| Fonctions | . | Opérations internes | Opérations externes (*) |
| Applications | Transformations | Lois (de composition) internes | Lois (de composition) externes (*) |
| Bijections | Permutations | (**) | . |
- Remarques
- (*) à gauche ou à droite.
- (**) Les relations ternaires internes ne peuvent être des bijections que si le cardinal de leur ensemble d’arrivée est infini ou égal à 0 ou à 1.
Nous retrouvons dans ce tableau les deux familles de notions définies plus haut, relations et fonctions, et leurs combinaisons :
- Une transformation dans un ensemble est une application de cet ensemble dans lui-même, donc une relation binaire dans cet ensemble ;
- Une permutation dans un ensemble est une bijection d’un ensemble dans lui-même, donc une relation binaire dans cet ensemble. C’est donc un cas particulier de transformation ;
- Une opération est une correspondance qui est à la fois une relation ternaire et une fonction ;
- Une loi de composition (appellation souvent abrégée en loi) est une correspondance qui est à la fois une relation ternaire et une application. Les lois sont donc des opérations particulières.
Ainsi, les quatre opérations de notre enfance (+, −, ×, ÷) sont effectivement des opérations internes dans