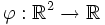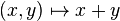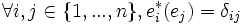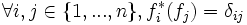Forme linéaire - Définition
En algèbre linéaire, les formes linéaires désignent un type particulier d'applications linéaires. L'étude spécifique qu'on leur accorde est motivée par le fait qu'elles jouent un rôle primordial en mathématiques, et en analyse, par exemple dans la théorie des distributions, ou dans la théorie des espaces de Hilbert.
Définition
En algèbre linéaire, une forme linéaire sur un espace vectoriel


En d'autres termes,


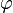


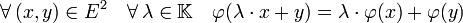
Remarques
- L'ensemble des formes linéaires sur



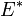
- L'application constante de valeur
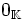
Exemples
est une forme linéaire sur
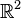
- Si L1(Ω) est le

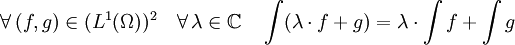
Base duales et antéduales
L'ensemble des formes linéaires sur un espace vectoriel

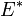


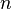
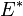
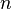

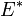
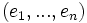

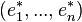
(où δij est le symbole de Kronecker, c'est-à-dire valant 1 si i = j et 0 sinon). Ces formes linéaires sont aussi appelées les projections des coordonnées, l'image d'un vecteur x par
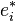
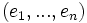
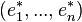
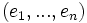
Inversement, si on se donne une base
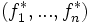
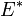
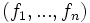

La base
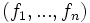
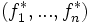
Propriétés algébriques
- Si
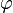
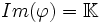
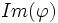
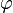
- Si
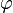
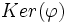

- Réciproquement, si
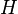

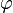
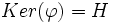
- Enfin, une propriété importante est que deux formes linéaires ont le même noyau si et seulement si elles sont proportionnelles.
Formes linéaires continues
Si on considère un espace vectoriel normé

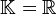

- Si

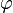
Formes linéaires continues sur un espace de Hilbert
On suppose désormais que


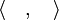
On démontre que les formes linéaires continues sur

-
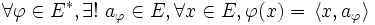
Grâce à Riesz.
| Articles de mathématiques en rapport avec l'algèbre linéaire |
| Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire |