Pseudovecteur - Définition

Introduction

En physique et en mathématiques, un pseudovecteur ou vecteur axial est un objet mathématique qui se comporte de la même manière qu'un vecteur pour une rotation directe (conservant les angles orientés) mais qui change de sens lors d'une isométrie indirecte comme, en dimension 3, une inversion de tous les axes ou une symétrie par rapport à un plan.

Ce changement de sens se traduit dans une base orthonormale par un changement de signe des coordonnées du pseudovecteur. On parle de pseudovecteurs en opposition aux vecteurs dits vrais ou polaires, qui sont invariants par une telle inversion.

Les règles de calcul concernant les pseudovecteurs sont ainsi différentes de celles des vecteurs vrais. La raison en est qu'un pseudovecteur, même s'il possède comme un vecteur trois composantes liées au système de coordonnées choisi, n'est pas un vecteur, mais un objet mathématique appelé forme différentielle de degré 2 (ou 2-forme), que l'on peut représenter comme une matrice tridimensionnelle et antisymétrique, possédant donc trois composantes indépendantes.

Généralités

On rencontre fréquemment des pseudovecteurs construits à partir d'un produit vectoriel.

Si a et b sont deux vecteurs vrais, l'objet p défini par

,

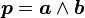
est un pseudovecteur : si on transforme tous les axes en leurs opposés, les vecteurs sont transformés en leurs opposés. a est donc remplacé par -a et b par -b. Si p était un vecteur, son image par cette transformation devrait être -p, or, en utilisant la formule de calcul du produit vectoriel, on s'aperçoit que p est invariant par une telle transformation : p n'obéit donc pas à toutes les règles de calcul des vecteurs ; on dit que p est un pseudovecteur.

Ce concept peut être généralisé : on parlera de pseudoscalaires et de pseudotenseurs pour des quantités qui ne respectent pas toutes les règles de calcul des scalaires et des tenseurs.

L'opérateur rotationnel, produit vectoriel avec l'opérateur nabla, construit également des pseudovecteurs.

La notion de pseudovecteur est particulièrement importante dans l'analyse des propriétés de symétrie des champs de vecteurs. Ainsi, si le champ électrique E (vecteur vrai) possède les mêmes symétries que ses sources (un plan de symétrie des charges est plan de symétrie de E), le champ magnétique B inverse ces propriétés (un plan de symétrie des courants est plan d'antisymétrie de B).

Un pseudovecteur est un tenseur d'ordre 2 antisymétrique et possède trois composantes dans un espace à trois dimensions.

Types

Il existe trois types de pseudovecteurs construits par produit vectoriel :

• les produits vectoriels de deux vecteurs, qui sont deux fois contravariant
• les produits vectoriels d'un vecteur et d'un covecteur, qui sont 1 fois covariant, 1 fois contravariant
• les produits vectoriels de deux covecteurs, qui sont deux fois covariant.

Le terme contravariant ou covariant fait référence à la manière dont réagissent les coordonnées du vecteur ou du covecteur lors d'un changement de base. Par exemple les coordonnées d'un vecteur évoluent inversement aux vecteurs de base. Les vecteurs sont donc dit contravariant. Les covecteurs, eux, sont covariant par rapport à la base des vecteurs. Cela pour assurer que le produit scalaire d'un vecteur et d'un covecteur soit bien scalaire, c'est-à-dire indépendant de la base des vecteurs.

Les pseudovecteurs des trois types appartiennent à des espaces vectoriels différents et l'addition de pseudovecteurs de types différents n'est donc pas permise.

Signification

Les pseudovecteurs peuvent être utilisés pour représenter :

• des angles dans un plan de l'espace (pseudovecteurs 1-fois covariant 1-fois contravariant : c'est-à-dire ceux dont la norme est un scalaire vrai, comme les angles). Intuitivement, ces pseudovecteurs correspondent à une notion d'angle dans un plan de l'espace.
• des éléments de surfaces orientées dans l'espace (pseudovecteurs 2-fois contravariant : leur norme est un scalaire doublement contravariant, comme les aires)
• une répartition surfacique en un point de l'espace. (pseudovecteurs 2-fois covariant, équivalents à des formes bilinéaires alternées)

L'idée qui relie les trois significations est celle de plan, de surface plane.

Exemples physiques

Exemples de pseudovecteurs en physique :

• Le moment angulaire ;
• Le champ magnétique en électromagnétisme ;
• Le rotationnel d'un champ de vecteurs ;
• La vitesse angulaire.

Ces trois pseudovecteurs sont 1 fois covariant, 1 fois contravariant. Leur norme est donc invariante par homothétie de la base, ce n'est pas le cas pour la norme des vecteurs.

Le produit vectoriel du pseudovecteur vitesse angulaire et du vecteur rayon jusqu'au centre de rotation donne la vitesse du point considéré : c'est la formule de Varignon.

Le produit vectoriel du pseudovecteur accélération angulaire et du rayon vecteur donne l'accélération du point considéré.