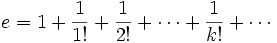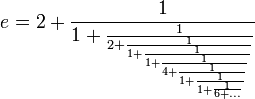E (nombre) - Définition

La constante mathématique e (parfois appelée constante de Néper du nom du mathématicien écossais John Napier qui introduisit les logarithmes) est la base des logarithmes naturels. Le nombre e appelé nombre exponentiel par Euler en 1761, vaut approximativement :

e ≈ 2,718 281 828 459 045 235 360 287 4...

Considérations historiques

Le nombre e est avec le nombre π, la constante réelle probablement la plus importante des mathématiques puisqu'on va la retrouver dans la normalisation des fonctions exponentielles. Il est cependant difficile de dater avec exactitude son apparition dans la littérature. En effet, si Neper introduit les logarithmes comme artifice de calcul pour simplifier les calculs de sinus, de cosinus, de produit et de quotient, il ne précise pas de base particulière pour ces logarithmes et les logarithmes les plus naturels sont ceux de base 10.

Les logarithmes naturels apparaissent pour la première fois en 1618 en appendice d'un traité de Napier probablement rédigé par William Oughtred.

En 1624, Briggs donne l'approximation du logarithme décimal d'un nombre qu'il n'identifie pas avec précision mais qui se révèle être e.

En 1647, Grégoire de Saint-Vincent calcule l'aire sous l'hyperbole mais ne met pas en évidence le nombre e.

En 1661, Huygens est capable de faire le rapprochement entre l'aire sous l'hyperbole et les fonctions logarithmes. Comme e est le réel tel que l'aire sous l'hyperbole entre 1 et e vaille 1, il est probable que ce nombre fut remarqué à cette époque sans toutefois que l'on parle pour lui de la base du logarithme naturel.

La première apparition de e comme nombre remarquable date de 1683, époque à laquelle Bernoulli s'intéresse aux calculs d'intérêt . Ce qui l'amène à étudier la limite de la suite . Mais personne à ce moment ne fait le rapprochement entre ce nombre et les logarithmes naturels. Pourtant c'est durant cette période que l'on commence à entrevoir que la fonction logarithme de base a est la réciproque de la fonction exponentielle de base a. La communauté scientifique est alors mûre pour découvrir e. C'est dans une lettre de Leibniz à Huygens que ce nombre est enfin identifié comme la base du logarithme naturel mais Leibniz lui donne le nom de b.

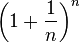
On doit la notation e pour cette constante à Euler dans une lettre que celui-ci adresse à Goldbach en 1731. Le choix de e a donné lieu a de nombreuses conjectures : e comme Euler ? e comme Exponentielle ? ou tout simplement e comme première voyelle disponible dans le travail d'Euler. C'est aussi Euler qui donne le développement de e en série

et en fraction continuée :

Puisque e possède un développement en fraction continuée infini il est donc irrationnel.

Mais c'est Hermite en 1873 qui prouve que e est transcendant.

Définitions et propriétés

Définitions de e

Les considérations précédentes montrent que e peut être défini de plusieurs façons différentes

• e est le réel tel que ln(e) = 1 pour ceux qui définissent la fonction ln comme la primitive de la fonction qui s'annule en 1. C'est la raison pour laquelle cette constante est aussi appelée la base des logarithmes naturels
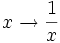
• e est le réel tel que exp(1) = e pour ceux qui définissent la fonction exp comme l'unique fonction vérifiant u'= u et u(0)=1.
• e est la limite de la suite .
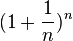
• e est la limite de la suite (avec la convention 0! = 1).

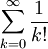
L'équivalence de ces trois définitions provient des relations qui lient la fonction exp, la fonction ln et les limites de suites.

Les cent premières décimales de e : 2,7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274

Théorie des nombres

La constante de Néper apparaît largement dans la théorie des nombres. Les mathématiciens se sont très tôt intéressés à la nature du nombre e. L'irrationalité de e fut démontrée par Lambert en 1761 et plus tard par Euler. La démonstration de l'irrationalité de e peut se faire grâce à son développement en série (voir *Démonstration de l'irrationalité de e) soit par son développement en fraction continuée.

La preuve de la transcendance de e fut établie par Hermite en 1873. On en déduit naturellement que, pour tout entier n et même pour tout rationnel r, eⁿ et e^r sont aussi transcendants, mais on ne sait pas encore (2007) si e^e est transcendant ou non.

Les propriétés de ce nombre sont à la base du Théorème de Lindemann-Weierstrass.

Il a été conjecturé que e était un nombre normal ou aléatoire.

Fonction exponentielle et équation différentielle

Pour tout réel x, exp(x) = e^x où exp est l'unique fonction vérifiant l'équation différentielle y' = y et y(0)= 1. Cette fonction est appelée fonction exponentielle de base e

Elle permet de donner toutes les solutions de l'équation différentielle y' = ay qui sont les fonctions définies par f(x) = Ce^ax

Fonction trigonométrique

La recherche de l'unique solution complexe à l'équation différentielle u' = iu et u(0) = 1 conduit à la fonction u(x) = e^ix = cos(x) + isin(x) et à l'identité d'Euler :

e^iπ + 1 = 0

qui selon Richard Feynman est " la formule la plus remarquable du monde ". Euler lui-même aurait également été émerveillé de cette relation rassemblant cinq nombres fondamentaux : 0, 1, e, i, π.