Loi de Poisson - Définition
En statistique, la loi de Poisson de paramètre λ, ou loi des événements rares, correspond au modèle suivant:
Sur une période T, un événement arrive en moyenne λ fois. On appelle X la variable aléatoire déterminant le nombre de fois où l'événement se produit dans la période T. X prend des valeurs entières : 0, 1, 2, ...
Cette variable aléatoire suit une loi de probabilité définie par
-
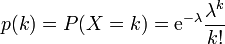
où
- e est la base de l'exponentielle (2,718...)
- k! est la factorielle de k
- λ est un nombre réel strictement positif
C'est la loi de Poisson de paramètre λ
Calcul de p(k)
Ce calcul peut se faire de manière déductive en travaillant sur une loi binomiale de paramètres (T; λ/T). Pour T grand, on démontre que la loi binomiale converge vers la loi de Poisson.
Il peut aussi se faire de manière inductive en étudiant sur l'intervalle [0; T] les fonctions Fk(t) = probabilité que l'événement se produise k fois sur l'intervalle de temps [0 ; t]. En utilisant la récurrence et du calcul différentiel, on parvient à retrouver les formules précédentes.
Espérance, variance, écart type
L'espérance d'une loi de Poisson est λ.
Si


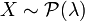
Alors, on a par définition que
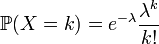
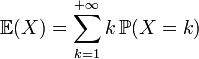
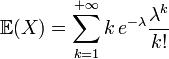
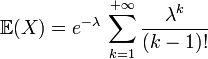
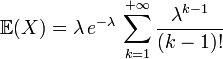
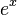
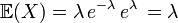
La variance d'une loi de Poisson est λ.
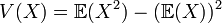
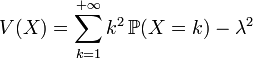
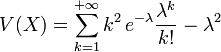
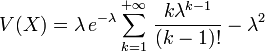
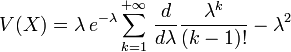
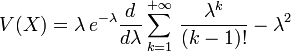
![V(X)=\lambda\,e^{-\lambda} \frac{d}{d\lambda}[\lambda\sum_{k=1}^{+{\infty}}\,\frac{\lambda^{k-1}}{(k-1)!}] - \lambda^2](https://static.techno-science.net/illustration/Definitions/autres/2/22877b4a0d89031e2d4fad5a281935ae_3c0d6a273c16b7c80703aed8d40aa43f.png)
![V(X)=\lambda\,e^{-\lambda} \frac{d}{d\lambda}[\lambda\,e^{\lambda}] - \lambda^2](https://static.techno-science.net/illustration/Definitions/autres/0/057f119c4a61811d7dd1040bde93d3ad_d88a8e6933674a2c4acf2212e16f1e16.png)
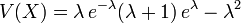
V(X) = λ(λ + 1) − λ2
V(X) = λ
Son écart type est donc
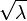
Fonction Caractéristique
La fonction caractéristique de la loi de poisson est
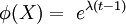
La fonction caractéristique d'une loi X se calcul par
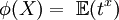
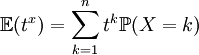
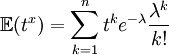
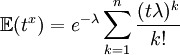
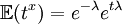
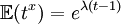
Domaine d'application
Le domaine d'application de la loi de Poisson a été longtemps limité à celui des événements rares comme les suicides d'enfants, les arrivées de bateaux dans un port ou les accidents dûs aux coups de pied de cheval dans les armées (étude de Ladislaus Bortkiewicz).
Mais depuis quelques décennies son champ d'application s'est considérablement élargi. Actuellement, on l'utilise beaucoup dans les télécommunications (pour compter le nombre de communications dans un intervalle de temps donné), le contrôle de qualité statistique, la description de certains phénomènes liés à la désintégration radioactive (la désintégration des noyaux radioactifs suivant, par ailleurs, une loi exponentielle de paramètre noté aussi lambda), la biologie, la météorologie, …
Diagrammes en bâtons
Comme toute loi de probabilité discrète, une loi de Poisson peut être représentée par un diagramme en bâtons. Ci-dessous sont représentés les diagrammes en bâtons des lois de Poisson de paramètres 1, 2 et 5.
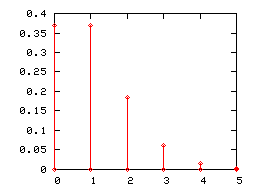
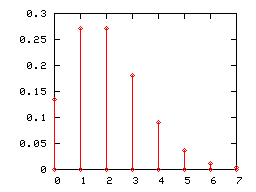
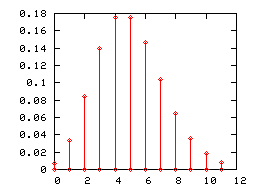
Lorsque le paramètre λ de la loi de Poisson devient grand, (pratiquement lorsqu'il est supérieur à 5), son diagramme en bâton est correctement approché par l'histogramme d'une loi normale d'espérance et de variance égales à λ (l'intervalle de classe étant égal à l'unité). Cette convergence était mise à profit, avant que les moyens informatiques ne se généralisent, pour utiliser la loi normale en lieu et place de la loi de Poisson dans certains tests.
Stabilité de la loi de Poisson par la somme
Si X et Y sont deux variables aléatoires indépendantes qui suivent des lois de Poisson de paramètres λ et μ, alors X+Y est une variable aléatoire qui suit la loi de Poisson de paramètre λ + μ.

















































