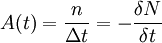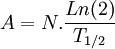Décroissance radioactive - Définition

Introduction

La décroissance radioactive est la réduction du nombre de noyaux radioactifs (instables) dans un échantillon. La décroissance radioactive se produit jusqu'à ce que tous les noyaux de l'échantillon soient stables.

Un radionucléide quelconque a autant de chances de se désintégrer à un moment donné qu'un autre radionucléide de la même espèce, et la désintégration ne dépend pas des conditions physico-chimiques dans lesquelles le nucléide se trouve. En d'autres termes, la désintégration est régie par le hasard, et la loi de désintégration radioactive est une loi statistique.

Loi de désintégration radioactive

Soit N(t) le nombre de radionucléides d'un élément donné présents dans un échantillon à un instant t quelconque. Comme la probabilité de désintégration d'un de ces radionucléides ne dépend ni de la présence d'autres radionucléides ni du milieu environnant, le nombre total de désintégrations dN pendant un petit intervalle de temps dt à l'instant t est proportionnel au nombre de radionucléides N présents et à la durée dt de cet intervalle : c'est une loi de décroissance exponentielle. Mathématiquement, cette loi s'écrit sous la forme :

dN = − λNdt

où la constante de proportionnalité λ, appelée constante radioactive du radionucléide considéré, possède la dimension de l'inverse d'un temps. On met le signe moins (–) parce que N diminue au cours du temps, de sorte que la constante λ est positive.

En intégrant l'équation différentielle précédente, on trouve le nombre N(t) de radionucléides présents dans le corps à un instant t quelconque, sachant qu'à un instant donné t = 0 il y en avait N₀ :

N(t) = N₀e ^{− λt}

Où:

• N₀ est le nombre initial de noyaux non-désintégrés ;
• λ est la constante radioactive de l'élément.

Activité moyenne

Activité d'un élément

On appelle « activité » le nombre de désintégrations par seconde d'un échantillon composé de N noyaux radioactifs. L'activité moyenne, notée A est exprimée en becquerel (Bq), qui représente le taux de désintégration des noyaux (nombre de désintégrations par secondes). On note :

Où:

• n est le nombre de noyaux qui se sont désintégrés durant une période Δt
• ΔN la variation du nombre de noyaux non désintégrés, qui sera fatalement négative pour une durée positive (Car les noyaux se désintègrent et donc leur nombre diminue).

En différenciant, on a immédiatement :

A = N₀.λ.e ^{− λ.t}

En remplaçant la constance radioactive λ par sa valeur exprimée en demi-vie, on voit que l'activité est inversement proportionnelle à la demi-vie de l'élément:

Le becquerel est une unité très petite. Quand un élément radioactif est présent en quantité métriques, le nombre d'atomes impliqués est de l'ordre du nombre d'Avogadro, soit 6x10^23. Pour un élément dont la demi-vie est d'un million d'années, soit 30x10^12 secondes, une mole de matière radioactive aura une activité de l'ordre de 20x10^9 Bq.

Activité d'un mélange dans le temps

D'une manière générale, un isotope radioactif présente une activité massique d'autant plus grande que sa demi-vie est brève. Les radioactivités fortes disparaissent donc rapidement, à échelle géologique. Les matières très radioactives ne le sont que pendant un temps relativement faible, et la radioactivité de vie longue (à échelle géologique) ne peut atteindre que des niveaux de radioactivité relativement faibles.

Dans le cas d'un mélange comme les produits de fission, au bout d'un certain temps de refroidissement, la radioactivité est dominée par les radioisotopes dont la demi-vie est de l'ordre de grandeur de ce temps de refroidissement : les radioisotopes dont la demi-vie est significativement plus courte se sont désintégrés plus rapidement, et leur niveau de radioactivité résiduel est négligeable ; et ceux dont la demi-vie est significativement plus longue sont moins radioactifs, et leur niveau de radioactivité est noyé par celui des éléments plus actifs.

Ainsi, dans le cas des produits de fission qui forment la majeure partie des déchets HAVL :

• Au bout d'une trentaine d'années, la radioactivité dominante est celle du césium 137 (30 ans) et du strontium 90 (28,8 ans), qui ont une activité massique de l'ordre de 3,3 et 5,2 TBq/g respectivement. Comme ces deux éléments représentent de l'ordre de 10% des produits de fission, les produits de fission ont alors une activité massique globale de l'ordre de quelques centaines de GBq/g.
• Au bout de quelques dix mille ans, la radioactivité dominante est celle du technétium 99 (211 000 ans), qui représente de l'ordre de 5% des produits de fissions. Son activité massique étant de 630 MBq/g, l'activité massique des produits de fissions est alors de l'ordre de 31 MBq/g.
• Comme aucun produit de fission n'a de durée de vie comprise entre cent et dix mille ans, l'activité du Technétium est celle des produits de fission pendant tout cet intervalle de temps.