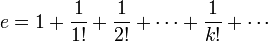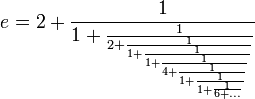E (nombre) - Définition

Introduction

la constante mathématique e
Logarithme naturel
Applications
Intérêts composés  · Identité d'Euler  · Formule d'Euler  · Demi-vie  · Croissance exponentielle / Décroissance exponentielle
Définitions
Démonstration de l'irrationalité de e  · Représentations de e  · Théorème d'Hermite-Lindemann
Personnes
John Napier  · Jacques Bernoulli  · Leonhard Euler
Conjecture de Schanuel

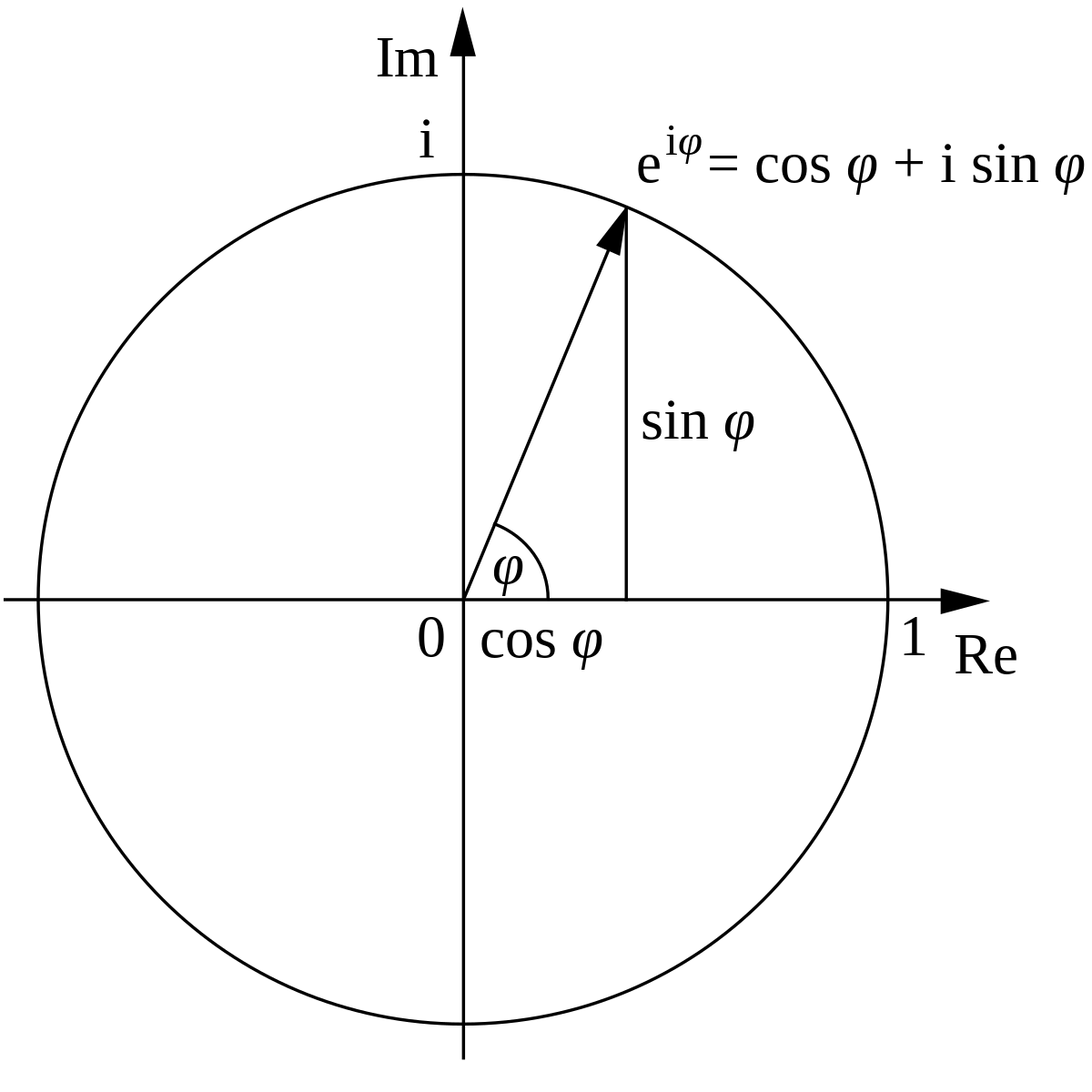
En mathématiques, e est une constante dont l'expression décimale commence par 2,718 281 828 459 045 235 360 287 4…. Il s'agit de la base des logarithmes naturels.

Appellation :

• e est parfois appelée constante de Néper, du nom du mathématicien écossais John Napier (ou Neper) qui introduisit les logarithmes.
• e fut appelé nombre exponentiel par Euler en 1761.

Considérations historiques

Le nombre e est probablement la constante réelle la plus importante des mathématiques après π : on la retrouve en effet dans la normalisation des fonctions exponentielles. Il est cependant difficile de dater avec exactitude son apparition dans la littérature. En effet, si Neper introduit les logarithmes comme artifice de calcul pour simplifier les calculs du sinus, du cosinus, du produit et du quotient, il ne précise pas de base particulière pour ces logarithmes et les logarithmes les plus courants à cette époque sont ceux en base 10.

Les logarithmes naturels apparaissent pour la première fois en 1618 en appendice d'un traité de Napier probablement rédigé par William Oughtred.

En 1624, Briggs donne l'approximation du logarithme décimal d'un nombre qu'il n'identifie pas avec précision, mais qui se révèle être e.

L'aire sous l'hyperbole est égale à 1 sur l'intervalle [1;e].

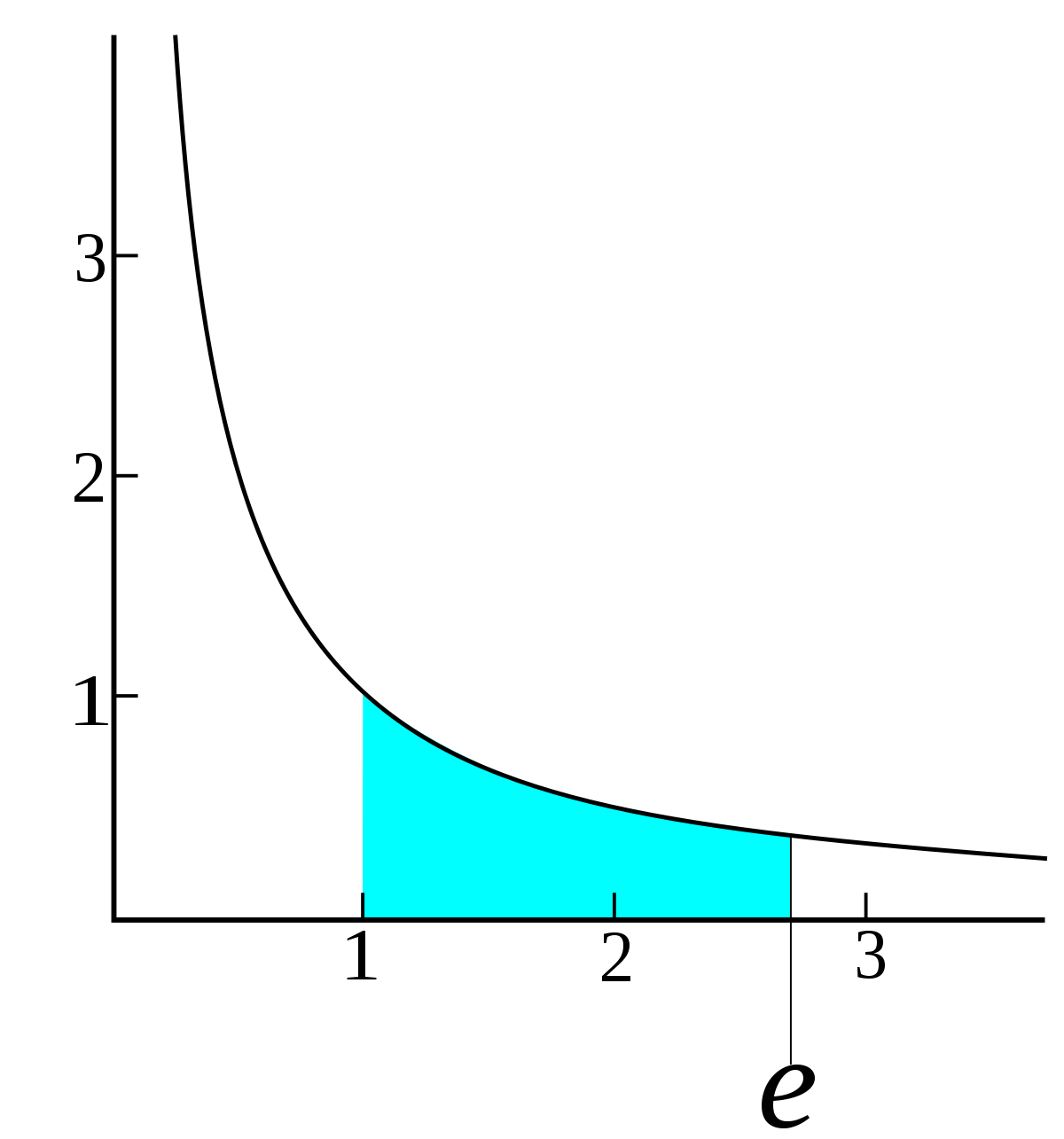
En 1647, Grégoire de Saint-Vincent calcule l'aire sous l'hyperbole, mais ne met pas en évidence le nombre e.

En 1661, Huygens est capable de faire le rapprochement entre l'aire sous l'hyperbole et les fonctions logarithmes. Comme e est le réel tel que l'aire sous l'hyperbole entre 1 et e vaille 1, il est probable que ce nombre fut remarqué à cette époque sans toutefois que l'on parle pour lui de la base du logarithme naturel.

La première apparition de e comme nombre remarquable date de 1683, époque à laquelle Bernoulli s'intéresse aux calculs d'intérêt. Ce qui l'amène à étudier la limite de la suite . Mais personne à ce moment ne fait le rapprochement entre ce nombre et les logarithmes naturels. Pourtant c'est durant cette période que l'on commence à entrevoir que la fonction logarithme de base a est la réciproque de la fonction exponentielle de base a. La communauté scientifique est alors mûre pour découvrir e. C'est dans une lettre de Leibniz à Huygens que ce nombre est enfin identifié comme la base du logarithme naturel, mais Leibniz lui donne le nom de b.

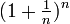
On doit la notation e pour cette constante à Euler dans une lettre que celui-ci adresse à Goldbach en 1731. Le choix de e a donné lieu a de nombreuses conjectures : e pour Euler ? e pour exponentielle ? ou tout simplement e comme première voyelle disponible dans le travail d'Euler.

C'est aussi Euler qui donne le développement de e en série

et en fraction continue :

Puisque e possède un développement en fraction continue infini, il est irrationnel. Les différents approximants de Padé permettent d'offrir de nombreuses expressions de e sous forme de fractions continues généralisées (cf. l'article Approximant de Padé de la fonction exponentielle). Elles permettent à Charles Hermite de démontrer la transcendance de ce nombre en 1873.

Décimales connues

Le nombre de décimales connues de la constante e a augmenté de façon spectaculaire au cours des dernières décennies. Cette précision est due à l'augmentation des performances des ordinateurs ainsi qu'au perfectionnement des algorithmes.