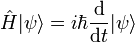Électrodynamique quantique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Mécanique quantique | ||||||||||||||
| | ||||||||||||||
| Postulats de la mécanique quantique Histoire de la mécanique quantique
| ||||||||||||||
L'électrodynamique quantique relativiste (QED en anglais) est une théorie physique ayant pour but de concilier l'électromagnétisme avec la mécanique quantique en utilisant un formalisme Lagrangien relativiste. Selon cette théorie, les charges électriques interagissent par échange de photons.
Description
L'électrodynamique quantique est une théorie quantique des champs de l'électromagnétisme. Elle décrit l'interaction électromagnétique des particules chargées et a été appelée le "bijou de la physique" (Richard Feynman ; Lumière & matière : une étrange histoire) pour ses prédictions extraordinairement précises dans la détermination théorique de quantités (mesurées par ailleurs) telles que l'anomalie de moment magnétique des leptons, ou encore le décalage de Lamb des niveaux d'énergie de l'hydrogène.
Mathématiquement, cette théorie a la structure d'un groupe abélien avec un groupe de jauge U(1). Le champ de jauge qui intervient dans l'interaction entre deux charges représentées par des champs de spin 1/2 est le champ électromagnétique. Physiquement, cela se traduit en disant que les particules chargées interagissent par l'échange de photons.
L'électrodynamique quantique fut la première théorie quantique des champs dans laquelle les difficultés pour élaborer un formalisme purement quantique permettant la création et l'annihilation de particules ont été résolus de façon satisfaisante.
Tomonaga, Schwinger et Feynman ont reçu en 1965 le prix Nobel de physique pour leur contribution à cette théorie, en particulier par la mise au point du calcul des quantités observables en utilisant la covariance et l'invariance de jauge.