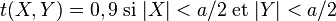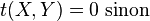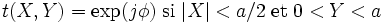Théorie de la diffraction - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie de la diffraction, dans sa forme élémentaire, repose sur le principe de Huygens-Fresnel. Selon ce principe, chaque point atteint par une onde se comporte comme une source secondaire. La figure de diffraction observée résulte de l'interférence des ondes émises par l'ensemble des sources secondaires. Bien que cette théorie ne fasse pas intervenir la nature de l'onde (sonore, lumineuse...), le vocabulaire et les illustrations de cet article seront empruntés au domaine de l'optique.
Le principe de Huygens-Fresnel est une approximation de la solution rigoureuse au problème de diffraction donnée par la résolution de l'équation d'onde. Il est valable dans le cadre de l'approximation paraxiale : c’est-à-dire quand la distance entre l'objet et la figure de diffraction est grande devant à la fois la taille de l'objet et la taille de la figure de diffraction.
Principe de Huygens-Fresnel
Enoncé
Soit une onde monochromatique incidente sur une ouverture. D'après le principe de Huygens-Fresnel, tout élément de surface de l'ouverture peut être considéré comme une source secondaire, se propageant de proche en proche (Huygens) et l'amplitude de l'onde émise par cette source secondaire est proportionnelle à la somme de chacun des éléments de surface de l'onde incidente (Fresnel). Les ondes émises par ces différentes sources interfèrent entre elles pour donner l'onde diffractée.
On trouve parfois une expression corrigée qui tient compte du fait qu'en toute rigueur la source ponctuelle n'est pas isotrope. Comme elle émet dans une direction privilégiée, on ajoute parfois un « facteur d'obliquité ».
Expression mathématique
On considère une ouverture (Σ) contenue dans le plan z = 0. Soit E(P) = E(X,Y) l'amplitude de l'onde incidente en un point P quelconque de l'ouverture, de coordonnées (X,Y). L'amplitude de l'onde émise par la source secondaire de surface dΣ autour de P est de la forme KE(P)dΣ où K est une constante qu'il n'est pas utile de chercher à déterminer ici.
Lorsqu'elle arrive au point d'observation M, de coordonnées (x,y) dans le plan z = r, cette onde a pour amplitude, en notation complexe :
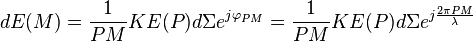
Le facteur 1/PM rend compte de l'atténuation de l'onde sphérique émise en P et
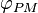
L'amplitude totale en M s'obtient en sommant les contributions de tous les points de l'ouverture, soit :
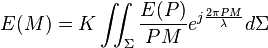
Facteur de transmission
Les objets diffractants ne sont pas forcément des ouvertures laissant passer 100% de l'onde au niveau de l'ouverture et rien à côté. Il peut s'agir d'objets atténuant l'onde de façon différente suivant le point considéré (diapositive par exemple, pour la lumière) et/ou d'objets introduisant un déphasage dépendant là aussi du point considéré.
Pour prendre en compte ces différentes possibilités, on introduit le facteur de transmission, ou transmission, t(P)=t(X, Y), d'un objet qui est le rapport entre l'amplitude de l'onde juste après l'objet avec celle de l'onde juste avant l'objet.
En notant E0(P) l'amplitude de l'onde juste avant l'objet diffractant, l'amplitude de l'onde diffractée s'écrit alors :
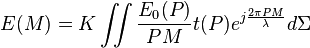
La transmission étant définie pour tout point P appartenant au plan de l'objet diffractant, les intégrales sont calculées de -∞ à +∞
Ce formalisme sera utilisé pour la .
Exemples:
- Ouverture carrée de côté a laissant passer 90% de l'onde.
- Un rayon lumineux incident à une distance y du sommet du prisme subit un déphasage φ=2πα y(n-1)/λ où λ est la longueur d'onde.
- En supposant le prisme parfaitement transparent, la transmission s'écrit:
-