Évaporation des trous noirs - Définition

Trous noirs et information

Le théorème no hair (de calvitie) qui énonce que seuls trois paramètres macroscopiques définissent l'état d'un trou noir pose un problème aux yeux de la théorie quantique. Si l'on envoie dans un trou noir un ensemble dit pur de particules, c'est-à-dire un faisceau cohérent (par exemple, un rayon laser, une paire de Cooper), le retour de cette énergie cohérente se fait sous la forme d'une énergie incohérente, une radiation thermique, un ensemble dit mixte. Or, les fonctions d'ondes qui décrivent ces deux types d'ensembles sont différents : dans le cas de l'ensemble pur les fonctions d'ondes s'additionnent vectoriellement, dans le cas d'un ensemble mixte, ce sont les carrés des modules des fonctions d'ondes qui s'additionnent. La transformation d'un ensemble en un autre n'est pas possible au sens quantique, puisqu'il ne s'agit pas d'une transformation unitaire (qui préserve la norme de la fonction d'onde).

D'où problème. Stephen Hawking a annoncé avoir résolu ce paradoxe, mais les détails de sa solution ne sont pas encore (02/2005) connus.

Temps d'évaporation

Il est possible d'estimer (avec des incertitudes, voir ci-dessous) le temps d'évaporation d'un trou noir. D'ordinaire, l'énergie rayonnée par un corps sphérique dont la température de surface est T et le rayon est R s'écrit

L = 4πR²σT⁴,

où σ est la constante de Stefan-Boltzmann. La perte d'énergie de masse d'un trou noir s'écrit donc en principe

.

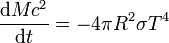
Pour un trou noir de Schwarzschild, ceci s'écrit

,

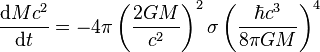
soit, en remplaçant la constante de Stefan-Boltzmann par sa valeur,

.

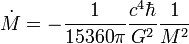
Le temps d'évaporation d'un trou noir de masse M s'écrit donc

.

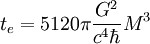
En unités de masses solaires, on obtient

.

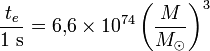
Une telle durée est environ 10⁵⁷ fois plus grande que l'âge de l'univers, illustrant le fait que l'évaporation de trous noirs stellaires est totalement négligeable. Par contre, des objets de masse 10¹⁹ fois plus faible qu'une masse solaire, soit de l'ordre d'un milliard de tonnes, ont un temps d'évaporation inférieur à l'âge de l'univers. Si de tels objets ont été produits lors du Big Bang, alors leur évaporation a lieu aujourd'hui.

Limites du calcul du temps d'évaporation

Si la dérivation ci-dessus est globalement correcte, elle comporte un certain nombre d'approximations qui la rendent inexacte. En particulier, la première équation (qui donne la perte d'énergie en fonction de la surface d'émission) s'avère incorrecte, car la quantité qui devrait intervenir n'est pas la surface, mais la section efficace d'un trou noir. D'ordinaire, ces deux quantités sont identiques à un facteur 4 près (la surface vaut 4 π R² et la section efficace π R²). Cependant, dans le cas d'un trou noir, la taille angulaire d'un trou noir est plus grande d'un facteur que ce qu'un calcul naïf donnerait. Ainsi, au lieu de l'aire du trou noir dans la formule ci-dessus, il faudrait rajouter un facteur 27/4.

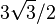
De plus, ce type de calcul est fait dans l'approximation de l'optique géométrique, où l'on suppose que les photons peuvent être assimilés à des particules ponctuelles, ou en tout cas de dimensions toujours très petites devant les autres dimensions du problème. Or dans le cas de l'évaporation des trous noirs, la longueur d'onde des photons est du même ordre que la taille physique du trou noir. Il conviendrait donc de se placer dans les calculs dans le cadre de l'optique physique, où serait prise en compte la forme exacte du front d'onde dans le champ gravitationnel du trou noir.

Enfin, il a été supposé ici que le trou noir émet uniquement des photons. En pratique, le phénomène d'évaporation concerne toutes les particules existantes, en tout cas toutes celles dont l'énergie de masse est inférieure à l'énergie typique des particules du rayonnement. En pratique, le trou noir rayonne aussi des gravitons, voire des neutrinos (si leur masse est suffisamment faible) en plus des photons. Vers la fin de sa vie, quand sa température atteint le domaine du gigaélectronvolt, il peut rayonner des quarks, des muons voire d'autres particules pour l'heure inconnues. Cependant, ces dernières étapes ne concernent la toute fin de l'évolution du trou noir. Les premiers calculs détaillés du taux d'évaporation ont été effectués par Don Page en 1976.

Au final, ces effets ne sont pas censés affecter le résultat général, mais pourraient le corriger d'un facteur numérique qui pourrait être fort différent de 1, mais il apparait peu probable qu'il s'éloigne de façon démesurée de 1. Aussi, le fait qu'un trou noir de masse stellaire ne puisse pas s'évaporer en un temps inférieur à l'âge de l'Univers est-il un résultat extrêmement robuste.