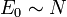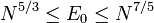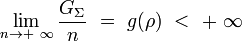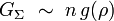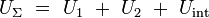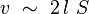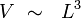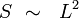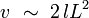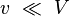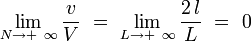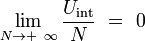Extensivité - intensivité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les variables extensives et intensives sont des catégories de variables physiques.
Prenons un exemple : si deux chevaux courent côte à côte et chacun à 60 km/h, à eux deux ils ne font pas un ensemble allant à 120 km/h, l'ensemble va aussi à 60 km/h (la vitesse est intensive), par contre à eux deux ils font un passage deux fois plus imposant qu'un cheval seul : le débit est doublé, la puissance aussi (ces deux variables sont extensives).
Le produit d'une variable intensive par une extensive donne une variable extensive ; le quotient de deux extensives donne une intensive.
Bien sûr, cette catégorisation est imparfaite : certaines variables ne sont pas parfaitement extensives. Par exemple, la masse d'un corps n'est pas la somme des masses de ses particules car une partie de leur masse est utilisée sous forme d'énergie de liaison. Il en est de même de variables intensives définies comme quotient de deux variables imparfaitement extensives.
Extensivité
Définition
En thermodynamique d'équilibre, un paramètre extensif (ou une grandeur extensive) est un paramètre caractérisant un système physique qui est proportionnel à la taille de ce système, ce dernier étant supposé à l'équilibre et homogène.
De manière générale, on dit d'une grandeur G qu'elle est extensive lorsque la somme des valeurs de cette grandeur pour deux systèmes disjoints est égale à la valeur de la grandeur pour la réunion des systèmes.
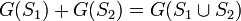
Pour cette raison on qualifie aussi souvent les grandeurs extensives d'additives bien que les deux termes ne soient synonymes qu'à la limite thermodynamique.
De la même manière on peut écrire que G est une variable extensive dépendant par exemple de la quantité de matière n et du volume V si :
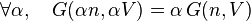
Exemples
On compte parmi les grandeurs extensives courantes :
- la masse ;
- le nombre de particules ;
- le volume (la surface, la longueur) ;
- la charge électrique ;
- l'avancement chimique ;
- l'entropie ;
- l'enthalpie ;
- le débit ;
- les forces.
En général une grandeur extensive est associée à au moins une grandeur intensive. L'association est d'ailleurs simple puisque le rapport de deux variables extensives est toujours une variable intensive.
La phrase : « une variable qui n'est pas extensive est une variable intensive », est fausse, car il existe des grandeurs ni extensives, ni intensives comme le carré du volume, par exemple, qui ne respectent pas la condition de linéarité. Même en faisant abstraction du cas académique où l'on prend une puissance arbitraire d'une quantité extensive, on trouve des systèmes thermodynamiques où des quantités fondamentales ne sont ni intensives ni extensives. Par exemple, en thermodynamique des trous noirs, la surface d'un trou noir est proportionnelle au carré de sa masse et non à sa masse. Sa variable conjuguée, la gravité de surface, proportionnelle à la température de Hawking n'est elle aussi ni extensive ni intensive.
Limite thermodynamique et approche mathématique
Soit un système Σ et une grandeur G définie par exemple par le nombre de particule n. G est dite extensive si et seulement si le rapport de G sur n a une limite finie quand n tend vers l'infini :
|
|
On appelle cela le passage à la limite thermodynamique. ρ = n / V est la densité du système, supposée indépendante de n. La grandeur g est alors une grandeur intensive associée à G et n.
On retrouve bien le fait qu'une grandeur extensive est, à la limite thermodynamique, proportionnelle à la taille du système :
|
|
Exemple : l'énergie interne
| Y a-t-il deux fois plus d'énergie dans deux litres d'essence que dans un litre ? |
La réponse à cette question, qui peut sembler anodine, n'est pas triviale du tout. Elle n'a de chance d'être positive qu'à la limite thermodynamique seulement ; en effet, l'énergie interne U d'un liquide ordinaire est une grandeur extensive bien qu'elle ne soit pas additive !
« Preuve » élémentaire
Considérons une partition du liquide (Σ) en deux sous-systèmes macroscopiques (Σ1) et (Σ2) ayant en commun la surface-frontière S. On peut écrire pour l'énergie interne du liquide (Σ) la relation exacte :
|
|
où :
- Ui est l'énergie interne du sous-système (Σi).
- Uint est l'énergie interne d'interaction, qui provient de la somme des énergies potentielles d'interactions entre certaines molécules du sous-système (Σ1) et d'autres du sous-système (Σ2) proches de la frontière, car dans un liquide ordinaire, les forces d'interaction entre molécules semblent à courte portée. La présence de cette énergie d'interaction non-nulle montre clairement que l'énergie interne n'est pas additive en général.
Montrons cependant que cette énergie d'interaction tend vers zéro à la limite thermodynamique des grands systèmes. Soit l la longueur caractéristique de la portée de l'interaction. Les molécules qui contribuent à l'énergie d'interaction Uint sont situées dans un volume v de l'ordre du produit de la surface de séparation S multiplié par la longueur 2 l :
|
|
Soit L une longueur caractéristique du liquide (Σ), de telle sorte que son volume total V soit de l'ordre de :
|
|
Alors, la surface de séparation S est de l'ordre de :
|
|
de telle sorte que le volume de la zone d'interaction est de l'ordre
|
|
Les forces d'interaction étant supposées à courte portée,
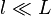
|
|
Plus précisément, il vient à la limite thermodynamique :
|
|
On aura donc une énergie d'interaction nulle à la limite thermodynamique :
|
|
Preuve rigoureuse ?
Dans la réalité, les molécules du liquide sont constituées à l'échelle fondamentale de protons, de neutrons et d'électrons, et ces particules interagissent essentiellement via des forces coulombiennes et gravitationnelles qui sont de portée infinie. Il n'est a priori pas du tout évident que les interactions intermoléculaires « résiduelles » soient bien à courtes portées, ce qui rend la « preuve » élémentaire précédente caduque. Plus grave, nous savons que la matière doit être décrite par la mécanique quantique à l'échelle microscopique.
- La première tentative sérieuse de preuve de l'extensivité de l'énergie interne a été proposée en 1950. Mais, dans le cadre de la mécanique statistique classique, cet auteur utilisait un potentiel d'interaction intermoléculaire de type « cœur-dur », donc peu réaliste.
- En 1969 a été démontré dans le cadre de la mécanique quantique qu'un système de N particules en interaction gravitationnelle possèdait un état fondamental d'énergie :
-
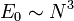
-
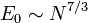
-
- Autrement dit, l'énergie interne n'est jamais extensive dans le cas d'interactions purement gravitationnelles, qui sont toujours attractives.
- En 1967, il a été montré que, dans le cadre de la mécanique quantique d'un système de N particules en interaction électrostatique, ce système possédait un état fondamental d'énergie :