Histoire de l'analyse fonctionnelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'analyse fonctionnelle est la branche des mathématiques et plus particulièrement de l'analyse qui étudie les espaces de fonctions. Sa naissance peut être datée à peu près à 1907, et, un siècle plus tard, elle est omniprésente dans toutes les branches des mathématiques, au point de ne plus vraiment être identifiable comme un domaine unifié de la recherche.

Avant 1903 : balbutiements
Sa naissance peut être datée à l'année 1748 quand Leonhard Euler publie son étude Introducto in Analysin Infinitorum dans laquelle il voulait considérer les « fonctions de variables » comme étant « objet de l'analyse », en exhibant diverses « espèces » de fonctions, bien qu'il indique ensuite un « moyen uniforme » de les traiter.
Après la première émission de cette idée, les mathématiciens développèrent principalement l'étude des fonctions continues, analytiques, puis elliptiques et autres catégories surgissantes de la physique mathématique ou de l'approfondissement de notions purement mathématiques.
Une équation intégrale d'une forme particulière émerge alors par sa généralité et sa difficulté : connaissant les fonctions
![\ f : [a;b] \to \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/0/09a255adc13719a4755df65d5a64766c_9ad1b9f1c120a3b5f65b60eedc0b4d49.png)
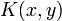
![\ \phi : [a;b] \to \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/7/7cb715dc23ab8780f0a4ea7cd83ffec4_ec745b96a7571fbe0d1ced63c2f25541.png)
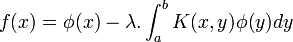
À la fin du 19e siècle, avec Hadamard, Lebesgue et Borel, sont développées les notions de d'intégrale de Lebesgue et de topologie.
Entre 1907 et 1920 : Riesz et Fréchet
La naissance de l'analyse fonctionnelle moderne peut être daté à 1907, entre la Hongrie, Göttingen et Paris, par les travaux quasi-simultanément publiés, complémentaires et se faisant écho de Frigyes Riesz (qui est hongrois), Ernst Sigismund Fischer (en), (de Göttingen), et Maurice Fréchet (qui est français).
En 1907, à l'aide des séries de Fourier, Riesz démontre « l'équivalence » entre un espace de suites (donc discret), et un espace de fonctions (donc continu) : ces espaces seront notés, par la suite,
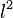
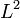
![\ L^2 \left( [0;2\pi] \right)](https://static.techno-science.net/illustration/Definitions/autres/8/8337d3c0bfcf49265cb9528626897bf5_7046cc13db00b20804c0a585b40010b8.png)
Quelques semaines après cette publication, Maurice Fréchet publie un article définissant :
- une topologie sur les fonctions à partir d'une notion de distance entre fonctions intégrables (au sens de Lebesgue) définies sur [0;2π] (définie dès sa thèse), et en utilisant la notion de convergence définie par Frédéric Riesz, l'année précédente, à partir de calculs semblables à la distance de Fréchet.
- le concept d'opérateur linéaire, en se limitant à ceux qui sont continus, dont il attribue l'invention à Jacques Hadamard.
L'outil principal utilisé par Fréchet est l'équivalence de Riesz, le théorème principal démontré est celui que l'on nomme aujourd'hui le théorème de représentation de Riesz dans le cas de l'espace
![\ L^2 \left( [0;2\pi] \right)](https://static.techno-science.net/illustration/Definitions/autres/8/8337d3c0bfcf49265cb9528626897bf5_7046cc13db00b20804c0a585b40010b8.png)
![\ L^2 \left( [0;2\pi] \right)](https://static.techno-science.net/illustration/Definitions/autres/8/8337d3c0bfcf49265cb9528626897bf5_7046cc13db00b20804c0a585b40010b8.png)
En 1908 se réunit, à Rome, le congrès international des mathématiciens où sont fixées des normes d'appellations et d'écritures afin d'assurer l'unité de ce domaine naissant mais non encore nommé. Les publications qui suivent, d'un bout à l'autre de l'Europe et aux États-Unis, respectent cette volonté d'unité.
En 1916, dans une publication, Riesz redéfinit l'ensemble des structures de manière abstraite et générale sur l'espace des fonctions continues sur un segment, la norme d'une fonction étant définie par
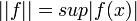
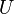
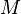
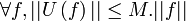
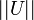
Ce travail topologise et algébrise cette théorie, et en même temps l'éloigne de la théorie des espaces vectoriels de dimension finie en montrant qu'en dimension infinie l'orthogonalité n'est pas toujours un support de travail, et que l'application identité n'y est pas compacte.

















































