Histoire de l'analyse fonctionnelle - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Avant 1903 : balbutiements - Entre 1907 et 1920 : Riesz et Fréchet - Entre 1903 et 1907 : de Fredholm à Hilbert - Entre 1936 et 1953 : Bourbaki - Entre 1920 et 1936 : méthodes de Banach et de Hilbert - À partir de 1973 : Enflo - À partir des années 1930 : algébrisation - À partir des années 1980 : éclatement de la discipline

Entre 1903 et 1907 : de Fredholm à Hilbert

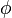
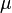
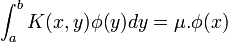
En 1903, Ivar Fredholm met au point une méthode pour résoudre l'équation intégrale ci-dessus dans certains cas : il s'agit d'exprimer la fonction cherchée à l'aide des fonctions $\ \phi$ vérifiant qu'il existe un nombre réel $\ \mu$ tel que $\int_a^b K(x,y) \phi (y) dy = \mu.\phi (x)$ , dans certains cas particuliers où le noyau permet de s'assurer de leur existence.

Entre 1903 et 1907, l'école mathématique de Göttingen, réunie autour de David Hilbert, utilise et développe cette méthode de Fredholm qui ressemble fort à la méthode d'algèbre linéaire pour résoudre un système d'équations. Ce faisant, il s'y développe une géométrisation discrète des espaces de fonctions (par le biais des séries de Fourier), notamment Hilbert introduit une forme quadratique utilisant les fonctions propres de ces équations intégrales et des extrema de valeurs propres, il donne alors une description des solutions de l'équation intégrale. C'est Erhard Schmidt qui épure la situation en 1905, dans sa thèse, en définissant directement un produit scalaire permettant une lecture d'espaces de fonctions comme des espaces euclidiens ayant une dimension infinie, et retrouve les solutions déjà énoncées par Hilbert, en utilisant ce que l'on nomme aujourd'hui « les fonctions propres de l'opérateur » (la notion générale d'opérateur n'est pas définie à cette date). Hilbert prend alors acte de ce progrès et réécrit toute sa géométrie pour pouvoir y inclure ces espaces de fonctions, il étudie $\ l^2 \left( [0;2\pi] \right)$ comme un espace vectoriel euclidien de dimension infinie dans lequel il envisage des formes bilinéaires symétriques bornées.

Entre 1936 et 1953 : Bourbaki

À partir de 1936, le groupe Bourbaki se réunit à Paris dans le but d'unifier les mathématiques, en partant du plus général, et, pour l'analyse fonctionnelle, en partant de la notion de dual topologique. Ce travail, mettant l'accent sur les espaces localement convexes, généralisant les œuvres antérieurs et considéré par beaucoup comme splendide, est déclaré achevé en 1953 par la publication d'un livre spécialement consacré à la dualité topologique. Le théorème de Krein-Milman et celui de Eberlein et Smulian en sont des éléments particulièrement importants, l'ensemble a pu être considéré comme un aboutissement des principales quêtes initiées dans les années 1920, incluant d'ailleurs la théorie des distributions.

Toutefois, certains manques se révèlent : à partir de 1953, Alexandre Grothendieck exhibe une foule d'espaces topologiques exotiques, inattendus ; et une algébrisation croissante ouvre de nouvelles voies de recherches.

Entre 1920 et 1936 : méthodes de Banach et de Hilbert

Banach

Après la Première Guerre mondiale, la Pologne renaissante décide de construire une école polonaise de mathématiques, comme un symbole de renaissance intellectuelle : l'attention se porte principalement sur la logique mathématique, la topologie et l'analyse fonctionnelle qui finit par être ainsi nommée. Durant plus de dix années d'efforts dans ce dernier domaine s'illustrent des mathématiciens tels que Hugo Steinhaus, Stanisław Saks, Otto Tœplitz et Ernst Hellinger. Puis, en 1932, Stefan Banach donne ses lettres de noblesse à cette école : il publie son livre Théorie des opérateurs linéaires.

Ce texte délaisse l'analogie entre les espaces vectoriels de dimension finie et les espaces de fonctions en exhibant différentes topologies possibles pour chaque espace de fonctions (alors qu'en dimension finie toutes les métriques définissent la même topologie). En englobant tous les travaux antérieurs, l'esprit de ce travail est pourtant bien différent de l'école de Göttingen : l'idée centrale est de faire de l'approximation une théorie pour pouvoir démontrer des théorèmes sur des ensembles de fonctions en se limitant à les démontrer sur des sous-ensembles denses et aux propriétés plus simples. Des exemples types de ce point de vue étant le théorème de Hahn-Banach, le théorème de Banach-Steinhaus et celui de l'application ouverte.

L'architecture de ce texte, particulièrement efficace, constitue aujourd'hui encore le socle théorique de ce domaine et certaines démonstrations restent celles d'origine, mais il n'en laisse pas moins des problèmes ouverts « d'ailleurs pas faciles à trouver », commente Banach, qui nourriront la recherche mathématique jusque dans les années 1970.

von Neumann

La même année 1932, John von Neumann publie Fondements mathématiques de la mécanique quantique, dont l'importance se fait encore sentir aujourd'hui à travers la géométrie non-commutative d'Alain Connes. Ce travail enrichit ceux de son professeur, Hilbert, en définissant les espaces hilbertiens sur le modèle de $\ L^2$ et ses opérateurs, en montrant tout leur intérêt et en ouvrant de nouvelles voies de recherches dépassant l'analyse fonctionnelle.

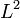
Deux écoles de pensée en rivalité

Les approches hilbertienne et banachique ont des lectures différentes de l'analyse fonctionnelle.

L'approche hilbertienne privilégie la régularité, notamment à travers l'étude des produits hilbertiens, dont la classification fut finie en 1935, ce que légitimait le théorème de représentation de Riesz et d'autres théorèmes dans la même veine permettant de ramener de nombreux problèmes à des études sur le même thème (théorème de Stone qui donne la structure des opérateurs dits "normaux", théorème de Lax-Milgram, méthode de Galerkin pour les équations différentielles, etc). L'utilité de ces résultats, notamment en physique quantique, valorisant ce travail.
L'approche banachique privilégie les "pathologies" en utilisant les propriétés d'approximation afin de cerner les raisons de leur divergence éventuelle, ce qu'illustrent surtout une lecture en contraposée de nombreux théorèmes banachiques, l'utilisation de l'existence de fonctions partout continues et nulle part dérivables, mais aussi, par exemple, la définition des espaces de Banach où n'intervient aucune autre structure algébrique que celle d'espace vectoriel normé.

Cette rivalité d'approches, qui tous comptes faits s'avèrent complémentaires, s'est poursuivie longtemps chez différents mathématiciens, comme l'illustrent le « sentiment de victoire » ressenti par l'école hilbertienne quand le théorème du point fixe de Schauder put être démontré par réduction au cas hilbertien le plus simple (Dunford-Schwartz, 1958), ou encore les efforts pour étendre l'analyse de type hilbertienne aux espaces fonctionnels à travers la création des espaces de Sobolev.