Histoire des polynômes - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Les fondements - Résolution générale des équations de degré n - Théorème fondamental de l'algèbre - Nombres algébriques

Théorème fondamental de l'algèbre

Dès cette époque, on cherche à découvrir les relations existant entre un polynôme et ses racines (nombres, formes, etc.). Viète met en évidence les relations existant entre les coefficients d'un polynôme et ses racines.

Le nombre de racines d'un polynôme pose problème. Les racines sont d'abord cherchées parmi les réels positifs puis parmi tous les réels. L'invention des nombres complexes par Bombelli (vers 1572) va permettre de trouver des racines à toute équation du second degré. La question suivante se pose alors : un polynôme de degré n possède-t-il toujours n racines ? René Descartes l'affirme sans le prouver. 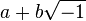La question est de savoir si les racines non réelles, dites imaginaires, sont toutes de la forme $a+b\sqrt{-1}$ . Jean Le Rond d'Alembert prouve en 1746 que toutes les racines doivent avoir la forme précédente. Cependant, sa démonstration n'est pas sans défaut, et il faut attendre Carl Friedrich Gauss (1777- 1855) et une incursion dans le domaine de l'analyse et la topologie pour prouver que tout polynôme de degré n à coefficients dans $\mathbb R$ possède exactement n racines dans $\mathbb C$ . C'est le théorème de d'Alembert-Gauss ou théorème fondamental de l'algèbre.

Nombres algébriques

La connaissances des polynômes à coefficients dans $\mathbb R$ semble être complète. Mais qu'en est-il des polynômes à coefficients dans $\mathbb Z$ ? Quels sont les réels ou les complexes qui peuvent être exprimés comme solution d'une équation de degré n à coefficients entiers ? L'étude des nombres algébriques est née, dominée par deux problèmes célèbres: celui des nombres constructibles à la règle et au compas et celui du dernier théorème de Fermat.

La question des nombres constructibles à la règle et au compas est un problème qui préoccupe les mathématiciens depuis l'époque d'Euclide. Quatre questions résistent encore au XVIII^e siècle : la trisection de l'angle, la duplication du cube, la quadrature du cercle et la constructibilité des polygones réguliers. C'est par le biais des polynômes et des extensions quadratiques (partant des nombres rationnels, on agrandit progressivement l'ensemble en y ajoutant des solutions d'équations du second degré à coefficients dans $\mathbb Q$ , puis à coefficients dans l'ensemble que l'on vient de créer et ainsi de suite) que la solution sera trouvée. Gauss décrit les polygones constructibles (Théorème de Gauss-Wantzel) et Pierre-Laurent Wantzel fait tomber les deux autres conjectures (la quadrature du cercle résistera quelque temps) et termine la démonstration de Gauss.

Le dernier théorème ou conjecture de Fermat - existe-t'il des solutions entières à une équation du type xⁿ+ yⁿ = zⁿ pour des degrés autres que 1 et 2 ?- a été démontré en 1994 par le mathématicien Andrew Wiles. Ce théorème aura nargué les mathématiciens depuis le XVII^e siècle. Nombreux sont ceux qui ont tenté de le résoudre par l'algèbre. Euler s'y cassa les dents. L'école allemande de la fin du XIX^e siècle avec Richard Dedekind, Ernst Kummer, David Hilbert, Emmy Noether va développer et approfondir le travail sur les polynômes, construisant la notion d'anneau, d'idéal, de corps, de nombres algébriques sans pour autant résoudre le problème. Cependant, ils ont ainsi fait faire aux mathématiques algébriques un saut considérable.

On peut à juste titre dire que les problèmes précédents, moteur des recherches sur les polynômes, ont contribué à la naissance et au développement de l'algèbre générale.