Lexique de la géométrie riemannienne - Définition

Introduction

La géométrie riemannienne est un domaine des mathématiques étudiant les propriétés des variétés riemanniennes. Cette page rappelle brièvement les définitions des termes récurrents rencontrés.

A

• Application conforme : Entre deux variétés riemanniennes, application qui préserve les angles ; de manière équivalente application qui transporte une métrique en une métrique conforme ;
• Application exponentielle : Application différentiable définie naturellement pour toute variété riemannienne complète, caractérisée par ce que exp(tv) soit la géodésique dont la vitesse au temps 0 est v ;

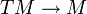
C

• Centre de masse
• Cercle osculateur
• Champ de Jacobi
• Champ de Killing
• Classe de Chern
• Convexité
• Courbure bisectionnelle
• Courbure de Gauss
• Courbure négative
• Courbure de Ricci
• Courbure sectionnelle
• Croissance d'un groupe
• Cut-locus d'un point m d'une variété riemannienne : Ensemble (négligeable) de points n pour lesquels il n'y a pas unicité de la géodésique minimisante ;

F

• Feuilletage riemannien : Feuilletage d'une variété en variétés riemanniennes ;
• Fibré normal : pour une sous-variété N d'une variété riemannienne M, fibré vectoriel sur N sont la fibre en x est l'orthogonal à T_xN ;
• Fibré riemannien : Fibé vectoriel muni d'une métrique riemannienne ;
• Flot géodésique : Flot différentiable sur l'espace tangent ou cotangent d'une variété riemannienne, ou sur le fibré en sphères correspondant, défini par la dynamique des géodésiques ;
• Fonction de Busemann : Fonction continue définie sur un espace (variété riemannienne ou espace métrique) à courbure négative bornée intervenant dans la compactification ; les fonctions de Buseman forment la sphère à l'infini ;
• Forme harmonique : Forme différentielle dont le laplacien est nul ;
• Forme de Kähler :
• Formule des traces de Selberg :

E

• Espace de Hadamard : Variété riemmannienne ou espace métrique simplement connexe de courbure strictement négative.
• Espace homogène : Variété sur laquelle agit transitivement un groupe de Lie.
• Espace symétrique : Variété riemannienne admettant en tout point au moins une involution.

H

• Holonomie
• Horosphère

G

• Géodésique : Courbe minimisant localement la distance sur une variété riemannienne ;
• Géodésique fermée : Géodésique périodique ;
• Géométrie euclidienne : géométrie d'un espace euclidien ;
• Géométrie riemannienne : Géométrie d'une variété riemannienne ;
• Groupe hyperbolique

L

• Laplacien : Opérateur différentiel défini sur toute variété riemannienne ;

I

• Identités de Bianchi : Identité remarquable portant sur la coubure de la connxion de Levi-Civita ;
• Inégalité de Bishop-Gromov : Estimation sur le volume des boules d'une variété riemannienne suivant des estimations sur la courbure de Ricci ;
• Inégalité isopérimétrique : Toute inégalité donnant une majoration du volume riemannien enfermé par une hypsersurface en fonction du volume de cette dernière ;
• Involution : Isométrie sur une variété riemannienne fixant un point et dont la différentielle en ce point est -Id ;
• Isométrie : Entre deux variétés riemanniennes, application différentiable envoyant métrique riemannienne sur métrique riemannienne ; ou de manière équivalent, application continue préservant les distances associée ;